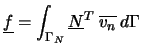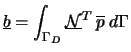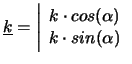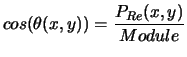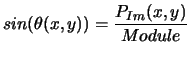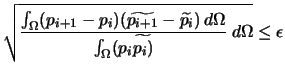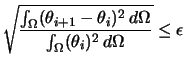


suivant: Calcul de l'erreur d'une
monter: Présentation de la méthode
précédent: Historique
Table des matières
Sous-sections
Aspects Théoriques
Cas d'un espace à une dimension
On introduit la fonction g(x) définie sur le domaine 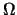 , dans l'espace de coordonnées X. Dans le cas d'un espace à une dimension, X signifie x; (x,y) dans un espace à 2 Dimensions et (x,y,z) en 3D.
, dans l'espace de coordonnées X. Dans le cas d'un espace à une dimension, X signifie x; (x,y) dans un espace à 2 Dimensions et (x,y,z) en 3D.
Dans un premier temps, il faut choisir une base de fonctions qui servira à construire l'interpolation. Cette base est constituée de monômes définis dans l'espace X. on note cette base P(X). On note m la dimension de cette base.
Voici, dans des espaces à 1 ou 2 dimensions des exemples de bases :
- Base linéaire 1D, m=2 :
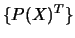 ={1,x}
={1,x}
- Base trigonométrique 1D, m=2 :
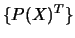 ={1,cos(x)}
={1,cos(x)}
- Base quadratique 1D, m=3 :
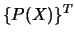 ={1,x,
={1,x,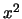 }
}
- Base linéaire 2D, m=3 :
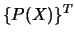 ={1,x,y}
={1,x,y}
- Base trigonométrique 2D, m=3 :
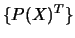 ={1,cos(x),cos(y)}
={1,cos(x),cos(y)}
- Base quadratique 2D, m=6 :
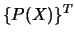 ={1,x,y,
={1,x,y,
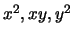 }
}
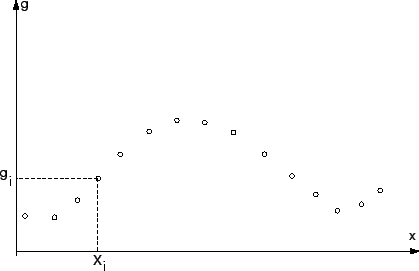
Construisons alors l'interpolation d'une fonction g(x) en dimension 1 :
Supposons connues les valeurs nodales 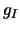 =g(
=g(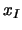 )
)
Figure 4.1:
Les N valeurs nodales de la fonction
|
|
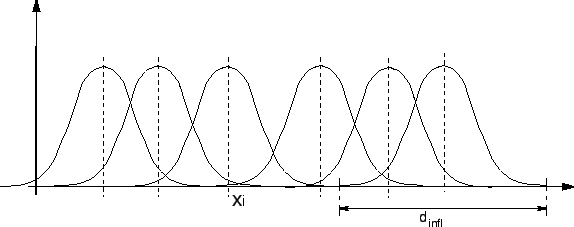
On définit ensuite pour chacun de ces noeuds un domaine d'influence caractérisé par son diamètre d'influence 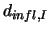 . On introduit aussi à chaque noeud une fonction de poids,
. On introduit aussi à chaque noeud une fonction de poids, 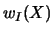 =
=
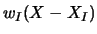 qui est positive sur le domaine d'influence du noeud, vaut 1 en
qui est positive sur le domaine d'influence du noeud, vaut 1 en 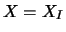 , et est nulle en dehors du domaine.
, et est nulle en dehors du domaine.
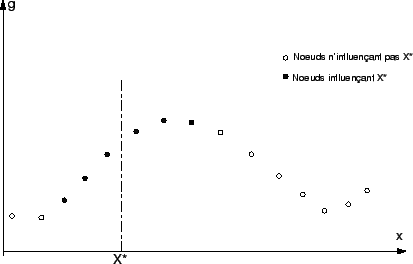
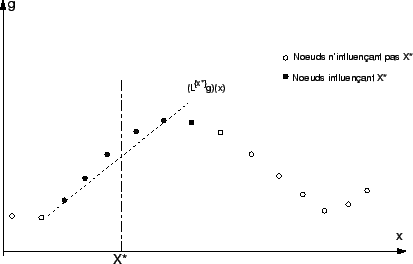
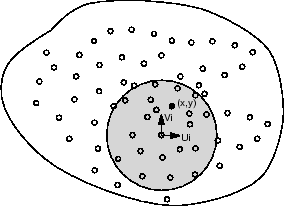
Déterminons l'approximation de la fonction g en un point  . Pour cela, on calcule en ce point les valeurs des fonctions de poids des n points qui influencent
. Pour cela, on calcule en ce point les valeurs des fonctions de poids des n points qui influencent  . (Ce sont tous les noeuds contenant
. (Ce sont tous les noeuds contenant  dans leur domaine d'influence.) (
dans leur domaine d'influence.) (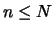 ).
).
Figure 4.2:
Noeuds influents
|
|
L'approximation des moindres carrés pondérés au voisinage de  peut s'écrire :
peut s'écrire :
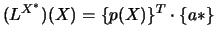 |
|
|
(4.1) |
On détermine les coefficients a* en minimisant l'expression suivante par rapport aux composantes 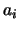 de a* :
de a* :
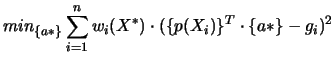 |
|
|
(4.2) |
On remarque que la spécificité de l'interpolation par moindres carrés pondérés est que le poids (donc l'influence d'un noeud) augmente si celui-ci est proche de X*. On obtient donc une courbe (dont l'ordre dépend de la base) qui ajuste au mieux les n noeuds influençant X*.
Le cas suivant est obtenu avec une base linéaire :
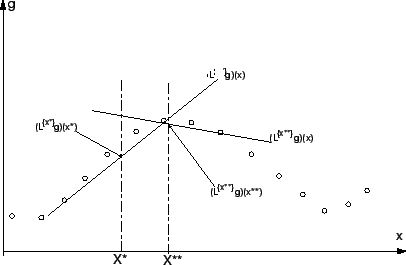
On peut ensuite réitérer cette approximation en un point X** quelconque :
Si on appelle
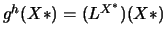 , on peut écrire cette fonction de X* comme une fonction de X, et donc :
, on peut écrire cette fonction de X* comme une fonction de X, et donc :
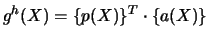 |
|
|
(4.3) |
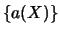 est évalué pour tout X en minimisant la norme
est évalué pour tout X en minimisant la norme 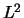 pondérée discrète suivante :
pondérée discrète suivante :
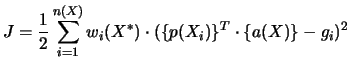 |
|
|
(4.4) |
avec
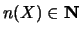 , le nombre de noeuds influençant le point de coordonnées X.
, le nombre de noeuds influençant le point de coordonnées X.
Il faut remarquer que les coefficients de {a(X)} sont variables.
L'interpolation 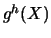 est donc une fonction non rationnelle
et non polynomiale même si sa base l'est. Dans le cas présenté, la
fonction interpolée est l'enveloppe de la famille de droites
définies en tout point X.
est donc une fonction non rationnelle
et non polynomiale même si sa base l'est. Dans le cas présenté, la
fonction interpolée est l'enveloppe de la famille de droites
définies en tout point X.
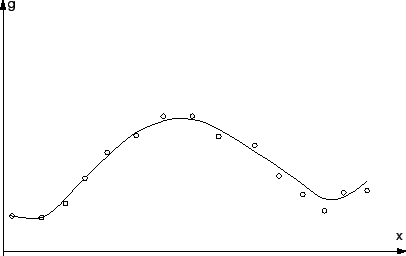 Résultat d'une interpolation par moindres carrés pondérés à coefficients variables.
Résultat d'une interpolation par moindres carrés pondérés à coefficients variables.
Détermination du vecteur {a(X)}
Pour déterminer les coefficients 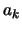 de {a(X)} (coefficients d'interpolation), il faut minimiser la norme J définie plus tôt (4.4). Cette minimisation s'écrit :
de {a(X)} (coefficients d'interpolation), il faut minimiser la norme J définie plus tôt (4.4). Cette minimisation s'écrit :
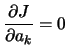 |
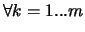 |
|
(4.5) |
En dévéloppant cette expression sous forme matricielle, on trouve :
![$\displaystyle \{a(X)\}=\left[A(X)\right]^{-1}\cdot \left[C(X)\right]\cdot \{g\}$](img95.gif) |
|
|
(4.6) |
Avec :
![\(\left[A(X)\right]\)](img96.gif) , matrice de (m x m)
, matrice de (m x m)
![$\displaystyle [A(X)]=\sum^{n}_{i=1}[w_{i}(X)\cdot \{p(X_{i})\} \cdot \{p(X_{i})^{T}]$](img97.gif) |
|
|
(4.7) |
et
![\(\left[C(X)\right]\)](img98.gif) , matrice de (m x m) :
, matrice de (m x m) :
![$\displaystyle [C(X)]=[w_{i}(X)\cdot \{p(X_{i})\},\cdots, w_{n}(X)\cdot \{p(X_{n})\}]$](img99.gif) |
|
|
(4.8) |
Expression des fonctions de forme
Connaissant {a(X)}, on peut maintenant obtenir 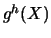 en fonction des valeurs à interpoler {g} :
en fonction des valeurs à interpoler {g} :
![$\displaystyle g^{h}(X)=\{p(X)\}^{T} \cdot \left[A(X)\right] \cdot \left[C(X)\right] \cdot \{g\}$](img100.gif) |
|
|
(4.9) |
On peut donc définir les fonctions de forme par le vecteur :
![$\displaystyle \{N_{1}(X),\cdots,N_{n}(X)\}=\{p(X)\}^{T} \cdot \left[A(X)\right] \cdot \left[C(X)\right]$](img101.gif) |
|
|
(4.10) |
Donc :
![$\displaystyle N_{i}(X)=\{\{p(X)\}^{T} \cdot \left[A(X)\right]^{-1} \cdot \left[C(X)\right]\}_{i}$](img102.gif) |
|
|
(4.11) |
La fonction interpolée en X peut donc s'écrire classiquement sous la forme :
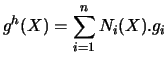 |
|
|
(4.12) |
On peut montrer que cette interpolation est consistante. La consistance quantifie la capacité d'une interpolation à représenter exactement toute fonction engendrée par l'espace {p(X)}.
De plus, il faut noter que
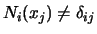 . On ne peut donc pas simplement forcer un déplacement, comme en éléments finis. C'est pourquoi on a introduit les multiplicateurs de Lagrange dans la formulation du problème (Chapitre 3.6).
. On ne peut donc pas simplement forcer un déplacement, comme en éléments finis. C'est pourquoi on a introduit les multiplicateurs de Lagrange dans la formulation du problème (Chapitre 3.6).
Passage en 2D
On peut ensuite facilement passer de l'exemple 1D à l'exemple 2D, en procédant de la même façon qu'en EF pour passer d'une modélisation poutre à une modélisation 2D.
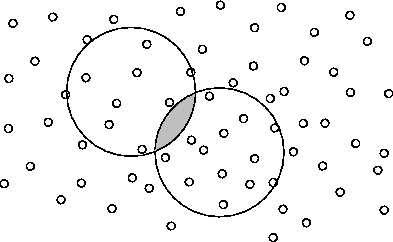
Cette fois-ci, le domaine d'influence est un cercle (ce n'est pas obligatoire. En effet, tout polygone convexe comme les carrés, les rectangles peut être utilisé pour délimiter les domaines d'influence).
Figure:
Domaines d'influence à 2 Dimensions
|
|
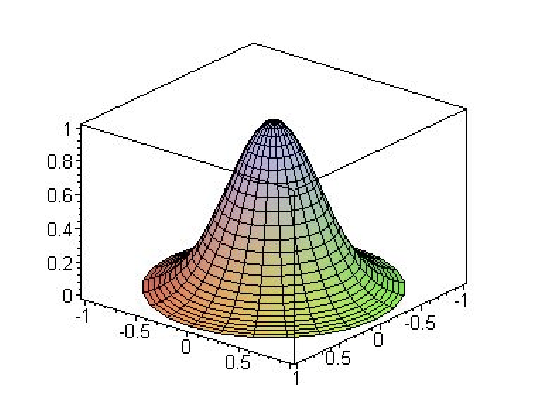
Figure 4.4:
Fonction de Poids en 2D (domaine d'influence circulaire)
|
|
Le vecteur des pressions nodales est noté 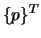 :
:
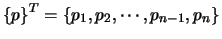 |
|
|
(4.13) |
On a, de plus :
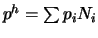 . Ce qui donne, comme en
EF la relation matricielle suivante :
. Ce qui donne, comme en
EF la relation matricielle suivante :
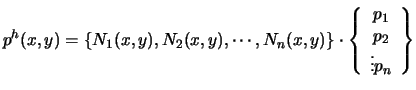 |
|
|
(4.14) |
On peut aussi écrire (4.14) sous cette forme :
![$\displaystyle p^{h}(x,y)=\left[N(x,y)\right] \cdot \{p\}_{d}$](img112.gif) |
|
|
(4.15) |
Avec :
![$\displaystyle N_{i}(x,y)=\{ \{p(x,y)\}^{T} \cdot \left[A(x,y)\right]^{-1} \cdot \left[C(x,y)\right]\}_{i}$](img113.gif) |
 |
|
(4.16) |
Condition nécessaire d'existence
On a vu précédemment (4.16) que le calcul des fonctions de formes imposait l'inversion de la matrice m x m
![\( \left[A(x,y)\right] \)](img115.gif) , mais cette matrice n'est pas toujours inversible.
On remarque cependant (4.7) qu'elle est la somme de n matrices de rang 1. Pour qu'elle soit inversible, il faut que son rang soit égal à m. Une condition nécessaire à cela est que chaque point soit influencé par au moins m noeuds. En effet, le rang d'une somme de matrices est inférieur ou égal à la somme des rangs de ces matrices, le rang de A est donc inférieur ou égal à n.
, mais cette matrice n'est pas toujours inversible.
On remarque cependant (4.7) qu'elle est la somme de n matrices de rang 1. Pour qu'elle soit inversible, il faut que son rang soit égal à m. Une condition nécessaire à cela est que chaque point soit influencé par au moins m noeuds. En effet, le rang d'une somme de matrices est inférieur ou égal à la somme des rangs de ces matrices, le rang de A est donc inférieur ou égal à n.
Il faudra donc avoir une taille de domaines telle que 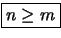
Ce qui est équivalent à :
Pour que l'interpolation par moindres carrés pondérés à coefficients variables soit définie sur tout le domaine considéré, il faut que le nombre de noeuds influençant tout point X soit au moins égal à la dimension de la base choisie pour l'interpolation.
Application au problème d'acoustique.
On approximera la pression et sa variation par :
![$\displaystyle p^{h}(x,y)=\left[N(x,y)\right] \cdot \{p\}$](img117.gif) |
![$\textstyle \delta p^{h}(x,y)=\left[N(x,y)\right] \cdot \{\delta p\}$](img118.gif) |
|
(4.17) |
On approximera aussi les multiplicateurs de Lagrange par :
![$\displaystyle \lambda ^{h}=\left[\mathcal{N} \right] \cdot \{\lambda \}$](img119.gif) |
![$\textstyle \delta \lambda^{h}=\left[\mathcal{N} \right] \cdot \{\delta \lambda\}$](img120.gif) |
|
(4.18) |
avec 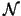 l'interpolant des multiplicateurs de Lagrange, qui ne doit pas obligatoirement être le même que pour N.
l'interpolant des multiplicateurs de Lagrange, qui ne doit pas obligatoirement être le même que pour N.
En introduisant (4.17) et (4.18) dans la formulation variationnelle, on obtient le système suivant :
![$\displaystyle \left[
\begin{array}{cc}\left[K\right]+j\:\rho\:c\:k\:\left[C\rig...
...ight\}
=
\left\{
\begin{array}{cc}-j\:\rho\:c\:k\:f\\
b\\
\end{array}\right\}$](img122.gif) |
|
|
(4.19) |
Avec :
- La matrice de "raideur"
![\(\left[K\right]\)](img123.gif) :
:
![$\displaystyle \left[K\right]=\int_{\Omega} \nabla \underline{N} ^{T} \underline{\nabla N}\:d\Omega$](img124.gif) |
|
|
(4.20) |
- La matrice "d'amortissement"
![\(\left[C\right]\)](img125.gif) (Conditions limites de Robin):
(Conditions limites de Robin):
![$\displaystyle \left[C\right]=\int_{\Gamma_{R}}\underline{N}^{T}\underline{N}\:A_{n}\:d\Gamma$](img126.gif) |
|
|
(4.21) |
- La matrice de "masse"
![\(\left[M\right]\)](img127.gif) :
:
![$\displaystyle \left[M\right]=\frac{1}{c^{2}}\int_{\Omega}\underline{N}^{T}\underline{N}\:d\Gamma$](img128.gif) |
|
|
(4.22) |
- La matrice
![\(\left[K\right]_{p\lambda}\)](img129.gif) de couplage des deux inconnues :
de couplage des deux inconnues :
![$\displaystyle \left[K\right]_{p\lambda}=\int_{\Gamma_{D}} \underline{N} ^{T} \underline{\mathcal{N}} \:d\Omega$](img130.gif) |
|
|
(4.23) |
- le vecteur des vitesses normales fixées
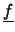 (Conditions limites de Neumann) :
(Conditions limites de Neumann) :
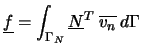 |
|
|
(4.24) |
- le vecteur des pressions fixées
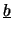 (Conditions limites de Dirichlet) :
(Conditions limites de Dirichlet) :
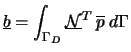 |
|
|
(4.25) |
- Le vecteur
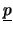 des pressions nodales
des pressions nodales
- Le vecteur
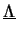 des multiplicateurs de Lagrange
des multiplicateurs de Lagrange
La résolution d'un problème d'acoustique en EFGM peut donc s'écrire sous forme de la résolution d'un système linéaire (4.19) (Comme en EF).
La présence de multiplicateurs de Lagrange augmente sensiblement la taille du système, donc son temps de résolution. Cependant, il est très rare qu'un cas où la pression est fixée se présente dans la réalité. L'utilisation de ces multiplicateurs, ne sera donc, dans la plupart des cas pas nécessaire.
Approximation d'onde localement plane.
On a vu précédemment
que l'un des avantages de la méthode meshless était de pouvoir
intégrer dans sa base une forme de la solution exacte du problème.
C'est, pour un grand nombre de méthodes de calculs numériques en
dynamique un des axes de recherche actuels. Des articles
([15]) ont déjà présenté des moyens d'annuler
l'erreur de pollution en acoustique 1D. Cette méthode se proposait
d'utiliser une base :
-
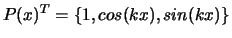 en 1D.
en 1D.
-
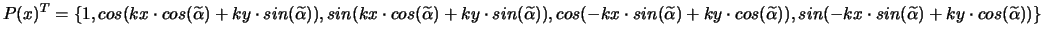 en 2D, pour éliminer l'erreur dans 2 directions (
en 2D, pour éliminer l'erreur dans 2 directions (
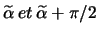 ).
).
Cependant, ces méthodes n'annulent l'erreur que pour un nombre fini d'angles de propagation (voir [13]) . Afin d'éliminer l'erreur quelque soit la direction de propagation, il faudrait que l'onde soit plane, et que l'on connaisse en chaque point
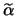 .
.
Or, une hypothèse physique commune consiste à considérer la propagation d'une onde quelconque comme plane localement. On peut donc écrire en chaque point M(x,y) :
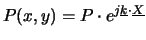 |
|
|
(4.26) |
Avec:
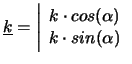 |
|
|
(4.27) |
d'où :
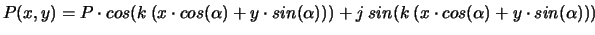 |
|
|
(4.28) |
En posant :
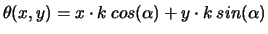 |
|
|
(4.29) |
On obtient finalement :
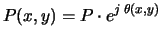 |
|
|
(4.30) |
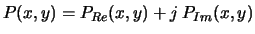 |
|
|
(4.31) |
On peut donc determiner 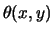 en tout point, une fois que l'on connaît le champ de pression :
en tout point, une fois que l'on connaît le champ de pression :
La démonstration de l'existence de cet angle 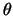 est donnée dans [VLacr]
est donnée dans [VLacr]
On construira donc une base
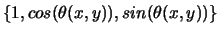 , ce qui permet une erreur minimale dans la solution approchée du problème.
Une approche multiniveaux procédera donc ainsi :
, ce qui permet une erreur minimale dans la solution approchée du problème.
Une approche multiniveaux procédera donc ainsi :
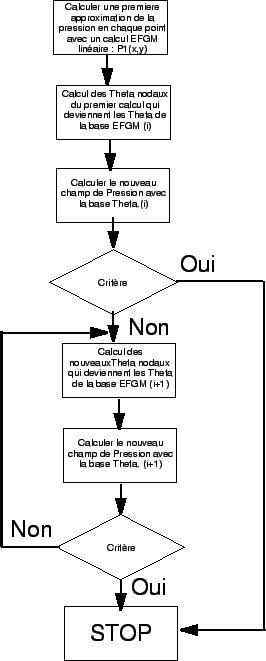
Figure 4.5:
Organigramme de l'approche Multiniveaux
|
|
Le critère utilisé dans cet algorithme peut être de deux types :
- Critère d'erreur globale en norme
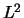 :
:
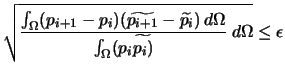 |
|
|
(4.33) |
- Critère de convergence de
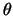 :
:
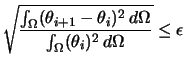 |
|
|
(4.34) |
En conclusion, on peut dire que cette méthode est prometteuse
([3]). En effet, elle permet d'annuler toute
erreur
de pollution sur le domaine considéré, mais cela, au prix d'un temps de calcul plus long qu'en meshless linéaire.



suivant: Calcul de l'erreur d'une
monter: Présentation de la méthode
précédent: Historique
Table des matières
greg
2001-08-07
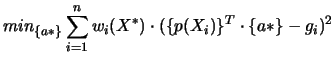
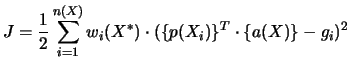

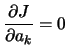
![$\displaystyle [A(X)]=\sum^{n}_{i=1}[w_{i}(X)\cdot \{p(X_{i})\} \cdot \{p(X_{i})^{T}]$](img97.gif)
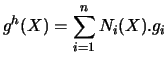
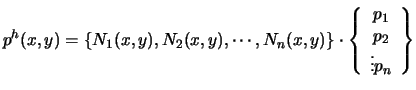
![$\displaystyle \left[
\begin{array}{cc}\left[K\right]+j\:\rho\:c\:k\:\left[C\rig...
...ight\}
=
\left\{
\begin{array}{cc}-j\:\rho\:c\:k\:f\\
b\\
\end{array}\right\}$](img122.gif)
![$\displaystyle \left[K\right]=\int_{\Omega} \nabla \underline{N} ^{T} \underline{\nabla N}\:d\Omega$](img124.gif)
![$\displaystyle \left[C\right]=\int_{\Gamma_{R}}\underline{N}^{T}\underline{N}\:A_{n}\:d\Gamma$](img126.gif)
![$\displaystyle \left[M\right]=\frac{1}{c^{2}}\int_{\Omega}\underline{N}^{T}\underline{N}\:d\Gamma$](img128.gif)
![$\displaystyle \left[K\right]_{p\lambda}=\int_{\Gamma_{D}} \underline{N} ^{T} \underline{\mathcal{N}} \:d\Omega$](img130.gif)