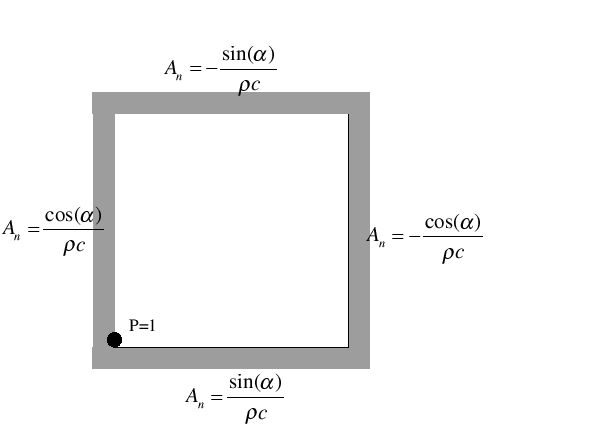
|
| (5.6) |
Avec ![]() , l'angle de propagation de l'onde, et
, l'angle de propagation de l'onde, et
![]() le nombre d'onde.
le nombre d'onde.
Les valeurs numériques des paramètres précédents sont :
On a ensuite réalisé une étude fréquentielle des erreurs relatives (sur p et ![]() ), par rapport à la solution exacte et EFGM de niveau 2.
), par rapport à la solution exacte et EFGM de niveau 2.
Cette étude est représentée dans la figure suivante :
On voit donc que, sur toute la bande de fréquence étudiée (50-700 Hz), l'indicateur d'erreur basé sur la solution EFGM de deuxième niveau semble donner satisfaction, puisque, hormis pour une fréquence de 420Hz, la courbe d'erreur globale relative à la solution exacte est très proche de celle de l'erreur relative à la solution EFGM de second niveau.
L'étude de l'indice d'efficacité de l'indicateur amène au même
constat :
En effet, pour qu'un indicateur soit considéré comme fiable, son indice d'efficacité doit être compris entre 0,8 et 1,2... Or, ici, on voit que cet indicateur est fiable, sauf pour deux fréquences 420 Hz, comme précédemment, mais aussi 400 Hz.
Concernant la différence à 420Hz environ, cette différence peu paraître inexplicable (250%) d'erreur !
Pour cerner la ou les sources de ce problème, étudions les évolutions des erreurs suivantes :
On voit, en étudiant la figure (5.8), que la solution EF commet deux pics d'erreur très marqués. Lors du premier, à 320Hz, l'erreur globale commise est de 139%. Cependant, le calcul EFGM de second niveau n'est pas trop affecté par ce pic. L'erreur de ce calcul par rapport à la solution exacte reste faible (2.3%), d'où le fait que les courbes d'erreur EF/Exacte et EF/EFGM restent très proches.
A 420Hz, par contre, il en est autrement : l'erreur commise par la solution EF/Exacte reste proche des 100% (120%), mais cette fois-ci, la solution EFGM de second niveau se dégrade beaucoup (pic d'erreur à 146%), alors qu'à part cette fréquence (sur une bande [0Hz,5OOHz]), l'erreur EFGM/Exacte est inférieure à 6%! Pourquoi?
Etudions maintenant les différentes erreurs sur la phase :
Étudions alors les cartes d'erreur sur la pression et la phase à cette fréquence.
En fait, il apparaît, si on regarde de plus près la solution EF que celle-ci est complètement incohérente à cette fréquence. On n'a plus, comme le montre la figure (5.4) de propagation sinusoïdale, mais quelquechose de totalement faux (pression variant entre -3 et 4, etc...).
Nous nous sommes penchés sur ce problème, et après une étude, on a
pu établir qu'il était indépendant du raffinement du maillage, du
type d'élément, de l'angle de propagation, mais qu'il semblait se
produire pour toutes les fréquences dont la longueur d'onde est
multiple de 0.2m. Par exemple pour une onde de célérité ![]() , on a le tableau suivant :
, on a le tableau suivant :
|
Les figures suivantes montrent l'évolution de la pression réelle et de la phase pour des fréquences proches de 400 et 420Hz.
On voit donc que la solution se dégrade peu à peu. Cette dégradation est plus visible avec un maillage plus raffiné. En effet, pour celui-ci, le fréquence aberrante est confondue avec celle calculée (tableau 5.1), alors que dans le cas du maillage précédent (400 éléments), la précision de calcul est plus faible.
|