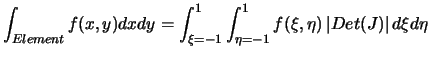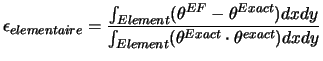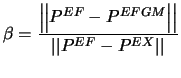


suivant: Exemple de la cavité
monter: Calcul de l'erreur d'une
précédent: Discrétisation et position du
Table des matières
Calcul d'erreur
Le calcul de l'erreur élémentaire revient à calculer, sur chaque
élément l'intégrale suivante (erreur élémentaire relative en norme
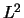 ):
):
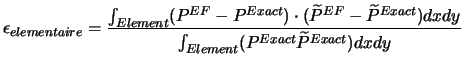 |
|
|
(5.1) |
Rem : 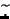 =Complexe Conjugué
=Complexe Conjugué
Pour Calculer ces intégrales,
on doit se ramener à l'élément parent, pour cela, on sait que :
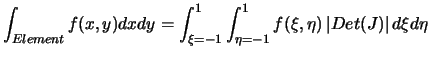 |
|
|
(5.2) |
Avec :
![$\displaystyle J=
\left[
\begin{array}{cc}
\frac{\partial x}{\partial \xi}&\frac...
... \eta}x_{i} & \frac{\sum \partial Ni}{\partial \eta}y_{i}\\
\end{array}\right]$](img165.gif) |
|
|
(5.3) |
Dans le cas du carré défini précédemment, on connaît 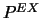 , mais dans la plupart des cas (dont celui de la voiture),
, mais dans la plupart des cas (dont celui de la voiture), 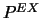 est inconnu. En élasticité, (par exemple, l'indicateur de Zienkiewicz [19]) on construit un champ lissé qui fait office de champ exact.
est inconnu. En élasticité, (par exemple, l'indicateur de Zienkiewicz [19]) on construit un champ lissé qui fait office de champ exact.
Le but de ce stage est de montrer que ce champ lissé peut-être
remplacé par la solution EFGM calculée à partir du champ de
pression EF.
Remarque : On introduit aussi l'erreur élémentaire relative sur la phase qui a l'expression suivante :
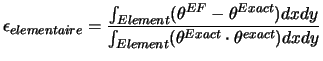 |
|
|
(5.4) |
Pour caractériser la qualité de l'indicateur d'erreur, on
introduit le coefficient d'efficacité de celui-ci :
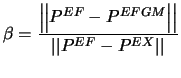 |
|
|
(5.5) |
On considèrera l'indicateur comme satisfaisant si son coefficient
d'efficacité est contenu dans l'intervalle
![$
\left[0.8,1.2\right]$](img169.gif) .
.



suivant: Exemple de la cavité
monter: Calcul de l'erreur d'une
précédent: Discrétisation et position du
Table des matières
greg
2001-08-07
![]() ):
):
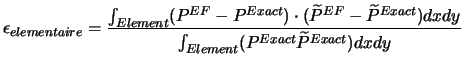
![]() =Complexe Conjugué
=Complexe Conjugué