| (3.5) |
Pour cela, on cherche la solution harmonique de l'équation des ondes (3.4). On postule donc que :
| (3.5) |
En remplaçant cette forme de solution dans l'équation des ondes (3.4), on obtient :
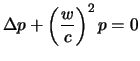 |
(3.6) |
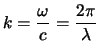 |
(3.7) |
Avec ![]() la longueur d'onde.
la longueur d'onde.
On trouve donc l'équation locale régissant l'acoustique (sous les
hypothèses définies en 3.1) (Equation de
Helmholtz):
On remarquera que la démonstration [1] de cette
équation permet de déterminer une relation entre la vitesse
acoustique et le gradient de pression :
Soit le domaine suivant :

On note ![]() la frontière de
la frontière de ![]() . Les parties
. Les parties
![]() et
et ![]() forment une partition de
forment une partition de
![]() , i.e. :
, i.e. :
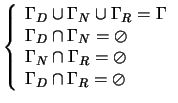
Avec sur ces différentes frontières, les conditions limites :
Condition limite de Dirichlet :
| (3.10) |
On note ![]() la valeur imposée de la pression.
la valeur imposée de la pression.
Condition limite de Neumann :
| (3.11) |
On note ![]() la valeur imposée de la composante
normale de la vitesse. Cette condition limite modélise la
vibration d'un panneau, ce qui en fait la condition la plus
souvent utilisée lorsque l'on a un couplage faible entre la
structure et le fluide. On effectue alors une étude vibratoire de
la structure, puis grâce à celle-ci une étude acoustique du fluide
sans se préoccuper des interactions fluide-structure.
la valeur imposée de la composante
normale de la vitesse. Cette condition limite modélise la
vibration d'un panneau, ce qui en fait la condition la plus
souvent utilisée lorsque l'on a un couplage faible entre la
structure et le fluide. On effectue alors une étude vibratoire de
la structure, puis grâce à celle-ci une étude acoustique du fluide
sans se préoccuper des interactions fluide-structure.
Condition limite de Robin :
| (3.12) |
![]() est appelé coefficient d'admittance. Il est relié à
l'impédance par la relation suivante :
est appelé coefficient d'admittance. Il est relié à
l'impédance par la relation suivante :
| (3.13) |