



Next: Square of liquid Alluminium
Up: Numerical examples in two
Previous: The way to integrate
Contents
The problem considered is a two-phase Stefan problem. The domain is a square
of length 2 m where the boundary conditions are following:
The material coefficients are :
This problem was solved using the adaptation of the generalized Trapezoidal
rule with
and a time step
.The initial solution
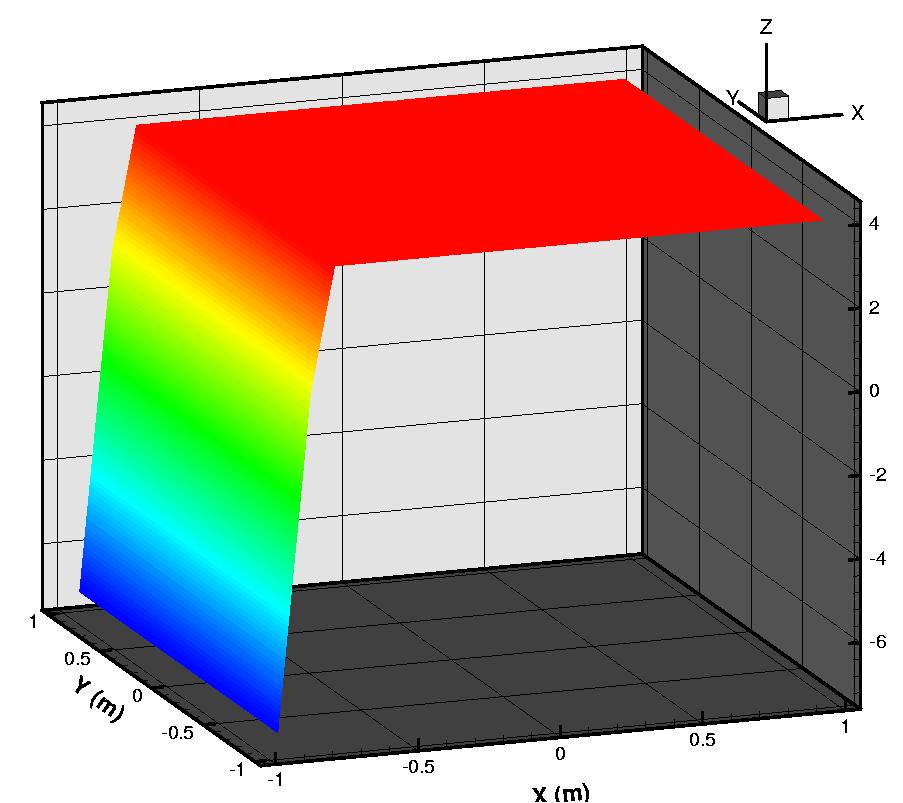
is composed by two planes, an horizontal one at and the other one
from to (see Fig. 32)
The interface is evolving from to
, case of the steady-state.
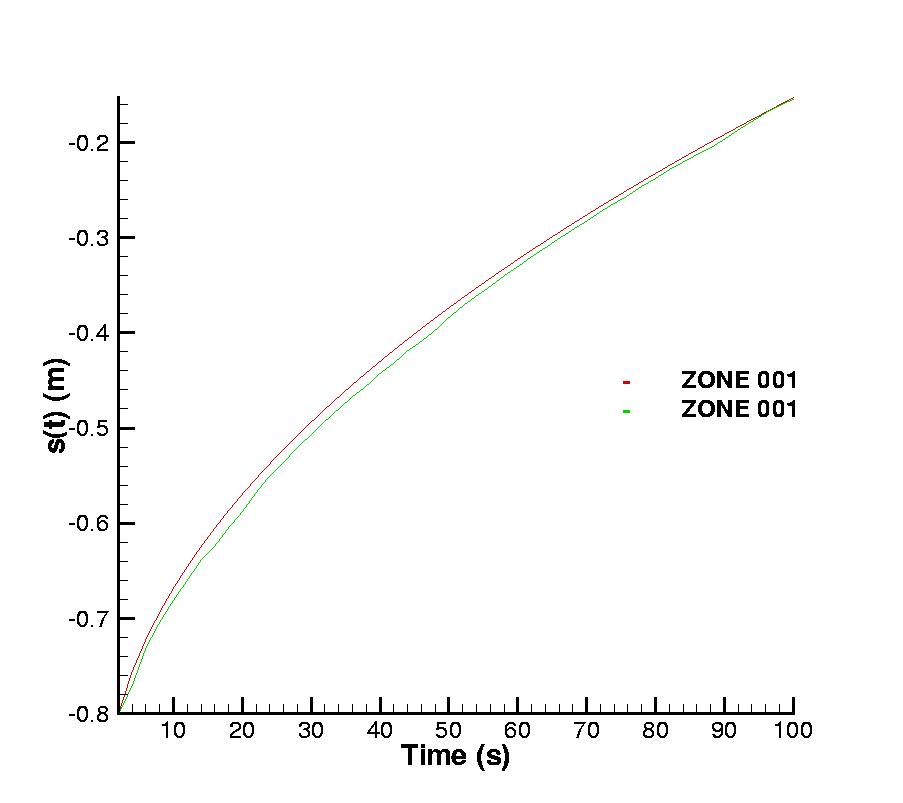
The figure 33 gives the evolution of the interface
with in comparison to the values given by [Lynch and
O'Neill, 1981]. The
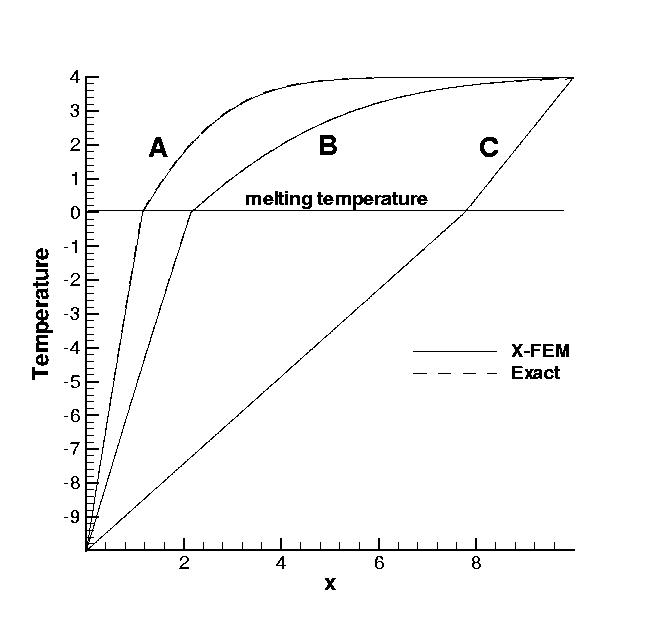
figure 34 gives the evolution of the profile of the
temperature during time. See the movie.
Figure 32:
The initial distribution.
|
Figure 33:
The evolution of the interface.
|
Figure 34:
The evolution of the profile for A)t = 180, B) t = 626 and C) steady-state.
|




Next: Square of liquid Alluminium
Up: Numerical examples in two
Previous: The way to integrate
Contents
Renaud Merle
2000-08-26
