PSI_Mat2_2015_26

  • Thème : construction de matrices, calculs de valeurs propres, simulations probabilistes, tracé de courbes, et diagonalisations.

Documentation

Correction d’un exercice de maths avec Python, issu des annales pour les oraux du concours Centrale-Supélec.

PSI_Mat2_2015_26.q0()[source]

Préliminaires :

>>> import numpy as np
>>> import numpy.linalg as LA  # Convention recommandée
>>> import matplotlib.pyplot as plt
  • On aura aussi besoin de faire des tirages aléatoires, on peut utiliser au choix soit numpy.random soit random. Je préfère le plus simple, random :
>>> import random
PSI_Mat2_2015_26.q1()[source]

Question 1.

  • On écrit d’abord une fonction qui créé cette matrice \(M(a, b)\),
  • Puis une fonction qui calcule ses deux valeurs propres complexes \(\lambda_1, \lambda_2\) (de façon approchée),
  • Et enfin, on renvoit ecart(a, b) = abs(lambda1 - lambda2).
PSI_Mat2_2015_26.M(a, b)[source]

Renvoie la matrice \(M(a, b)\) définie dans l’énoncé :

\[\begin{split}M(a, b) := [[3a - 2b, - 6a + 6b + 3], [a - b, - 2a + 3b + 1]] = \begin{bmatrix} 3a - 2b & - 6a + 6b + 3 \\ a - b & - 2a + 3b + 1 \end{bmatrix}\end{split}\]

Exemple :

>>> print(M(1, 3))
[[-3 15]
 [-2  8]]
PSI_Mat2_2015_26.lam12(a, b)[source]

Calcule et renvoie \(\lambda_1, \lambda_2 = \mathrm{Sp}(M(a, b))\).

Exemple :

>>> lam12(1, 3)
(2.0000000000000009, 2.9999999999999991)
>>> [round(l) for l in lam12(1, 3)]
[2.0, 3.0]
PSI_Mat2_2015_26.ecart(a, b)[source]

Calcule et renvoie \(|\lambda_1 - \lambda_2|\), approchée à \(10^{-2}\) près.

Exemple :

>>> ecart(1, 3)
1.0

Note

\(M(a, b)\) est diagonalisable ssi ses deux valeurs propres sont distinctes. Donc tester si ecart(a, b) est nul est un bon indicateur de la diagonalisabilité de \(M(a, b)\) (inexact mais presque correct). Cette idée relie les questions Q2.a, Q2.c, Q3.c.

PSI_Mat2_2015_26.q2()[source]

Question 2.

On passe à des simulations probabilistes.

PSI_Mat2_2015_26.q2_a()[source]

Question 2.a.

  • On va d’abord écrire une fonction geom() qui effectue un tirage selon une loi géométrique (de paramètre p),
  • Ensuite, la fonction hasard() est immédiate à écrire.

Note

hasard(p) / 500 est une valeur approchée de la probabilité que ecart(A, B) soit non-nul, soit que \(M(A, B)\) soit diagonalisable.

PSI_Mat2_2015_26.geom(p)[source]

Effectue un tirage selon une loi géométrique de paramètre p.

Par définition, en utilisant random.random(), on effectue ce tirage avec ce code :

n = 0
# Si 0 < p < 1, on est sûr que cette boucle termine (mais ça peut prendre du temps !)
while random.random() > p:
    # L'expérience de probabilité p a échoué, on compte +1
    n += 1
# On renvoie le nombre d'échec avant le succès
return n

Pour plus de détails, cf. cette page Wikipédia si besoin.

Note

Cette fonction est au programme, il faut la connaître !

Voir aussi

On aurait aussi pu utiliser numpy.random.geometric(), qui fonctionne directement :

>>> np.random.seed(0)  # On enlève l'aléatoire, pour que l'exemple soit le même à chaque fois
>>> p = 0.3  # Valeur arbitraire de p = 0.3
>>> a = np.random.geometric(p)
>>> b = np.random.geometric(p)
>>> ecart(a, b)
0.0
PSI_Mat2_2015_26.hasard(p, N=500)[source]

Fonction assez élémentaire : pour N = 500 fois, on tire a et b grâce à geom(), et on compte +1 si ecart() a donné ecart(a, b) >= 1e-1.

Voir aussi

En utilisant numpy.random.geometric(), on peut générer N = 500 tirages en une seule ligne :

>>> np.random.seed(0)  # On enlève l'aléatoire, pour que l'exemple soit le même à chaque fois
>>> p = 0.3  # Valeur arbitraire de p = 0.3
>>> N = 500
>>> a = np.random.geometric(p, N)
>>> b = np.random.geometric(p, N)
>>> # Cette sum( ecart(a[i], b[i]) >= 1e-1 ...) compte le nombre de ecart(a, b) qui sont >= 1e-1
>>> nb = sum(ecart(a[i], b[i]) >= 1e-1 for i in range(N))
>>> nb  # 434 sur 500
434
PSI_Mat2_2015_26.q2_b(N=500)[source]

Question 2.b.

  • On va d’abord créer la liste des valeurs de p \(= \frac{1}{100}, \dots, \frac{99}{100}\),
  • Puis pour chaque p, on calcule hasard(p) / 500 grâce à hasard(), qu’on stocke dans une liste de valeurs,
  • Enfin, on ouvre une fenêtre matplotlib et on affiche (avec matplotlib.pyplot.plot()) ces valeurs.

Attention

La fonction hasard() est, comme nom l’indique, aléatoire ! Donc chaque exécution de cette fonction sera différente, et donc chaque graphique sera différent !

Cela devrait donner une figure comme ça :

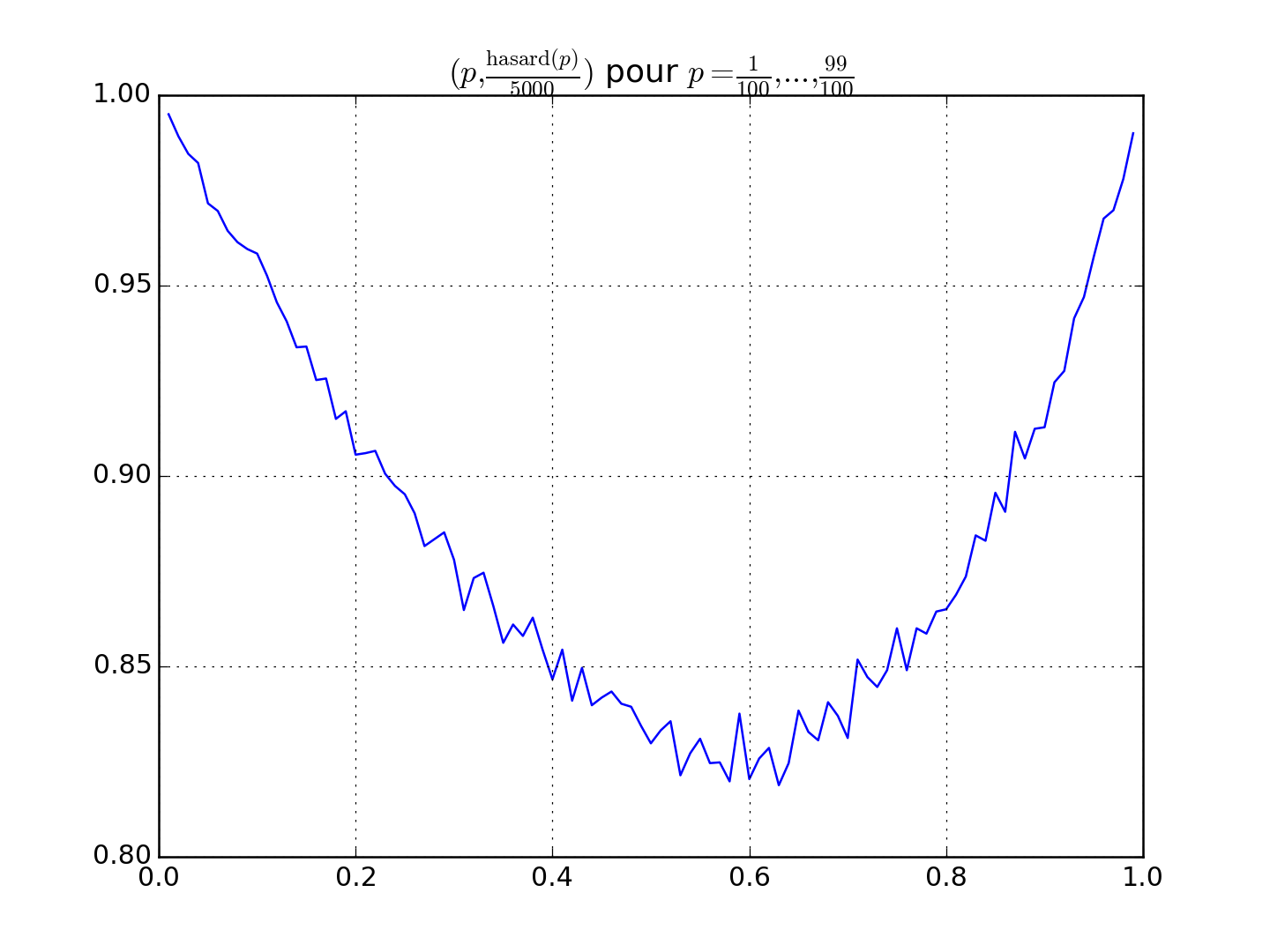
_images/PSI_Mat2_2015_26__figure1.png
PSI_Mat2_2015_26.q2_c(N=500)[source]

Question 2.c.

On a juste à ajouter trois lignes dans la fonction précédente Q2.b, en calculant les valeurs de \(\frac{2 - 2 p + p^2}{2 - p}\) pour p = np.linspace(1e-2, 1 - 1e-2, 400) (par exemple, pour 400 valeurs).

On est très content d’observer que cette formule colle très bien aux valeurs numériques simulées en Q2.b. (et donc, ça donne une très bonne indication pour la dernière question Q3.c).

Cela devrait donner une figure comme ça :

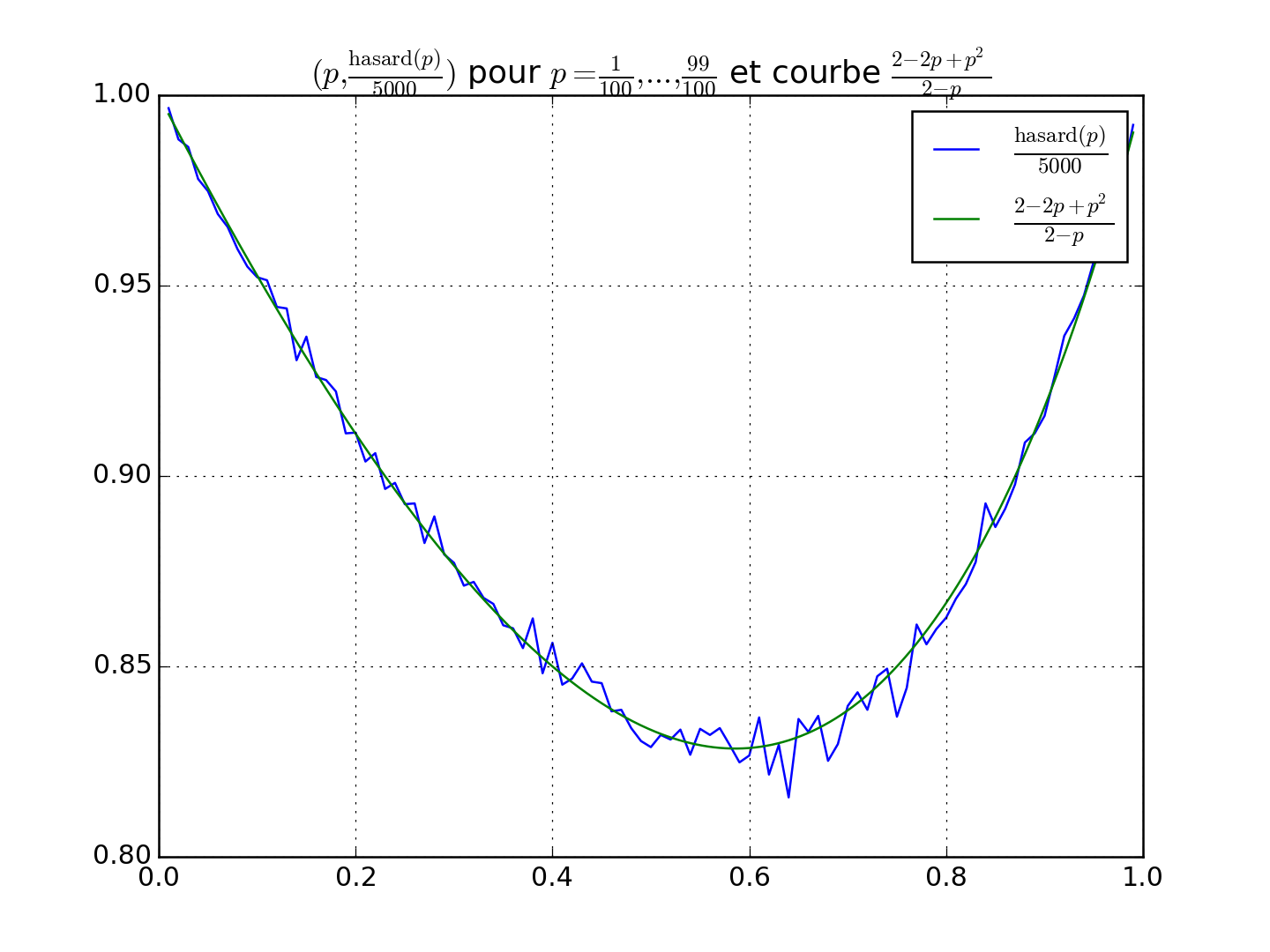
_images/PSI_Mat2_2015_26__figure2.png

Note

J’ai fait N = 5000 simulations plutôt que N = 500 pour mieux voir que la formule colle aux valeurs aléatoires.

PSI_Mat2_2015_26.q3()[source]

Question 3.

On définit la matrice \(M'(a, b)\) suivante :

\[\begin{split}M'(a, b) := [[a+1, 1], [0, b]] = \begin{bmatrix} a + 1 & 1 \\ 0 & b \end{bmatrix}\end{split}\]
PSI_Mat2_2015_26.q3_a()[source]

Question 3.a.

C’est une pure question de maths, à faire sur papier.

Pour des matrices \(2 \times 2\), si elles sont diagonalisables, il suffit de vérifier qu’elles ont même polynôme caractéristique (et qu’il soit scindé à racines simples), soit mêmes traces et mêmes déterminant :

  • Trace :
\[\begin{split}\mathrm{tr}(M(a, b)) &= (3a - 2b) + (-2a + 3b + 1) = a + b + 1. \\ \mathrm{tr}(M'(a, b)) &= (a + 1) + (b) = a + b + 1.\end{split}\]
  • Déterminant :
\[\begin{split}\mathrm{det}(M(a, b)) &= (3a - 2b) \times (-2a + 3b + 1) - (a - b) \times (-6a + 6b + 3) = b (a + 1). \\ \mathrm{det}(M'(a, b)) &= (a + 1) \times b - 0 \times 1 = b (a + 1).\end{split}\]

Note

Vous pouvez vérifier le calcul de \(\mathrm{det}(M(a, b))\) vous-même, ou par exemple sur ce site (SymPyGamma.com).

  • Si elles ne sont pas diagonalisables, en fait ça implique que \(a + 1 = b\), et donc en regardant la forme simplifiée de \(M(a, b)\) dans ce cas, on arrive assez vite à montrer qu’elle est semblable à \(M'(a, b)\).
PSI_Mat2_2015_26.q3_b()[source]

Question 3.b.

Une matrice réelle \(2 \times 2\) est diagonalisable ssi elle admet deux valeurs propres distinctes.

Donc la matrice \(M'(a, b)\) est diagonalisable ssi \(a + 1 \neq b\).

PSI_Mat2_2015_26.q3_c()[source]

Question 3.c.

D’après Q3.a et Q3.b, \(M(a, b)\) est diagonalisable ssi \(M'(a, b)\) l’est (elles sont semblables) ssi \(a + 1 \neq b\).

Calculons donc la probabilité que \(A + 1 \neq B\) (on rappelle que les deux variables aléatoires \(A\) et \(B\) suivent \(\mathcal{G}(p)\) une loi géométrique de paramètre \(p\)).

\[\begin{split}\mathbb{P}(A + 1 \neq B) &= \sum_{k=0}^{+\infty} \mathbb{P}(A + 1 \neq k, B = k) \\ &= \sum_{k=0}^{+\infty} \mathbb{P}(A \neq k - 1) \mathbb{P}(B = k) \;\;\text{car}\;A,B \;\text{indépendants}\\ &= \mathbb{P}(B = 0) + \sum_{k=1}^{+\infty} (1 - \mathbb{P}(A = k - 1)) ((1-p)^{k} p) \;\;\text{car}\;B \thicksim \mathcal{G}(p) \\ &= p + p \sum_{k=1}^{+\infty} (1 - ((1-p)^{k-1} p)) (1-p)^{k} \;\;\text{car}\;A \thicksim \mathcal{G}(p) \\ &= p + p \sum_{k=1}^{+\infty} (1-p)^{k} - p^2 \sum_{k=0}^{+\infty} (1-p)^{2k-1} \;\;\text{et}\;0 < (1-p) < 1 \\ &= p + p \frac{(1-p)}{1 - (1-p)} - p^2 \frac{1}{(1-p)} \frac{(1-p)^2}{1 - (1-p)^2} \\ &= p + (1-p) - \frac{p^2}{1-p} \frac{(1-p)^2}{2p-p^2} \\ &= 1 - \frac{p^2(1-p)^2}{p(2-p)(1-p)} \\ &= 1 - \frac{p(1-p)}{(2-p)} \\ &= \frac{(2-p) - p(1-p)}{2-p} \\ &= \frac{2-2p+p^2}{2-p}\end{split}\]

On retrouve bien la formule donnée par l’énoncé en Q3.c. OUF !

Sortie du script

$ python PSI_Mat2_2015_26.py
Test automatique de toutes les doctests ecrites dans la documentation (docstring) de chaque fonction :
Trying:
    print(M(1, 3))
Expecting:
    [[-3 15]
     [-2  8]]
ok
Trying:
    ecart(1, 3)
Expecting:
    1.0
ok
Trying:
    np.random.seed(0)  # On enlève l'aléatoire, pour que l'exemple soit le même à chaque fois
Expecting nothing
ok
Trying:
    p = 0.3  # Valeur arbitraire de p = 0.3
Expecting nothing
ok
Trying:
    a = np.random.geometric(p)
Expecting nothing
ok
Trying:
    b = np.random.geometric(p)
Expecting nothing
ok
Trying:
    ecart(a, b)
Expecting:
    0.0
ok
Trying:
    np.random.seed(0)  # On enlève l'aléatoire, pour que l'exemple soit le même à chaque fois
Expecting nothing
ok
Trying:
    p = 0.3  # Valeur arbitraire de p = 0.3
Expecting nothing
ok
Trying:
    N = 500
Expecting nothing
ok
Trying:
    a = np.random.geometric(p, N)
Expecting nothing
ok
Trying:
    b = np.random.geometric(p, N)
Expecting nothing
ok
Trying:
    nb = sum(ecart(a[i], b[i]) >= 1e-1 for i in range(N))
Expecting nothing
ok
Trying:
    nb  # 434 sur 500
Expecting:
    434
ok
Trying:
    lam12(1, 3)
Expecting:
    (2.0000000000000009, 2.9999999999999991)
ok
Trying:
    [round(l) for l in lam12(1, 3)]
Expecting:
    [2.0, 3.0]
ok
Trying:
    import numpy as np
Expecting nothing
ok
Trying:
    import numpy.linalg as LA  # Convention recommandée
Expecting nothing
ok
Trying:
    import matplotlib.pyplot as plt
Expecting nothing
ok
Trying:
    import random
Expecting nothing
ok
10 items had no tests:
    __main__
    __main__.q1
    __main__.q2
    __main__.q2_a
    __main__.q2_b
    __main__.q2_c
    __main__.q3
    __main__.q3_a
    __main__.q3_b
    __main__.q3_c
6 items passed all tests:
   1 tests in __main__.M
   1 tests in __main__.ecart
   5 tests in __main__.geom
   7 tests in __main__.hasard
   2 tests in __main__.lam12
   4 tests in __main__.q0
20 tests in 16 items.
20 passed and 0 failed.
Test passed.

Plus de details sur ces doctests peut etre trouve dans la documentation de Python:
https://docs.python.org/3/library/doctest.html (en anglais)

Le fichier Python se trouve ici : PSI_Mat2_2015_26.py.