PSI_Mat2_2015_24

  • Thème : tracé de courbes, développements limités, calcul d’équivalent.

Documentation

Correction d’un exercice de maths avec Python, issu des annales pour les oraux du concours Centrale-Supélec.

PSI_Mat2_2015_24.q0()[source]

Préliminaires :

  • Comme pour tous ces exercices, on commence par importer les modules requis, ici numpy et matplotlib :
>>> import numpy as np
>>> import matplotlib.pyplot as plt

>>> from scipy.integrate import quad
PSI_Mat2_2015_24.q1()[source]

Question 1.

On nous demandait de tracer, pour \(n = 2 \dots 7\), ces courbes \(\mathcal{C}_n = \{ (x_n(t), y_n(t)), t \in [0, 2\pi] \}\), définies par :

\[\begin{split}x_n(t) &= 4 \cos(t) - \cos(nt) \\ y_n(t) &= 4 \sin(t) - \sin(nt)\end{split}\]

Cela suggère d’utiliser une boucle for n in range(2, 7+1) et les fonctions généralisées numpy.cos() et numpy.sin() :

N = 300  # Nb points
t = np.arange(0, 2*np.pi, N)  # t = 0 .. 2*pi avec 300 points
plt.hold(True)  # Mettre tous les dessins sur la même figure
for n in range(2, 7 + 1):  # Rappel: range(a, b) = [a, a+1, .., a+b-1] borne b non incluse !
    x = 4 * np.cos(t) - np.cos(n * t)
    y = 4 * np.sin(t) - np.sin(n * t)
    plt.plot(x, y, label=("n = %d" % n))  # et pas (t, x) ou (t, y)
plt.legend()  # Afficher la légende, décrite avec les label=... plus haut
plt.title("Cn pour n = 2..7")  # On met un joli titre
plt.show()  # On montre la figure !

Cela donne une figure comme celle ci-dessous :

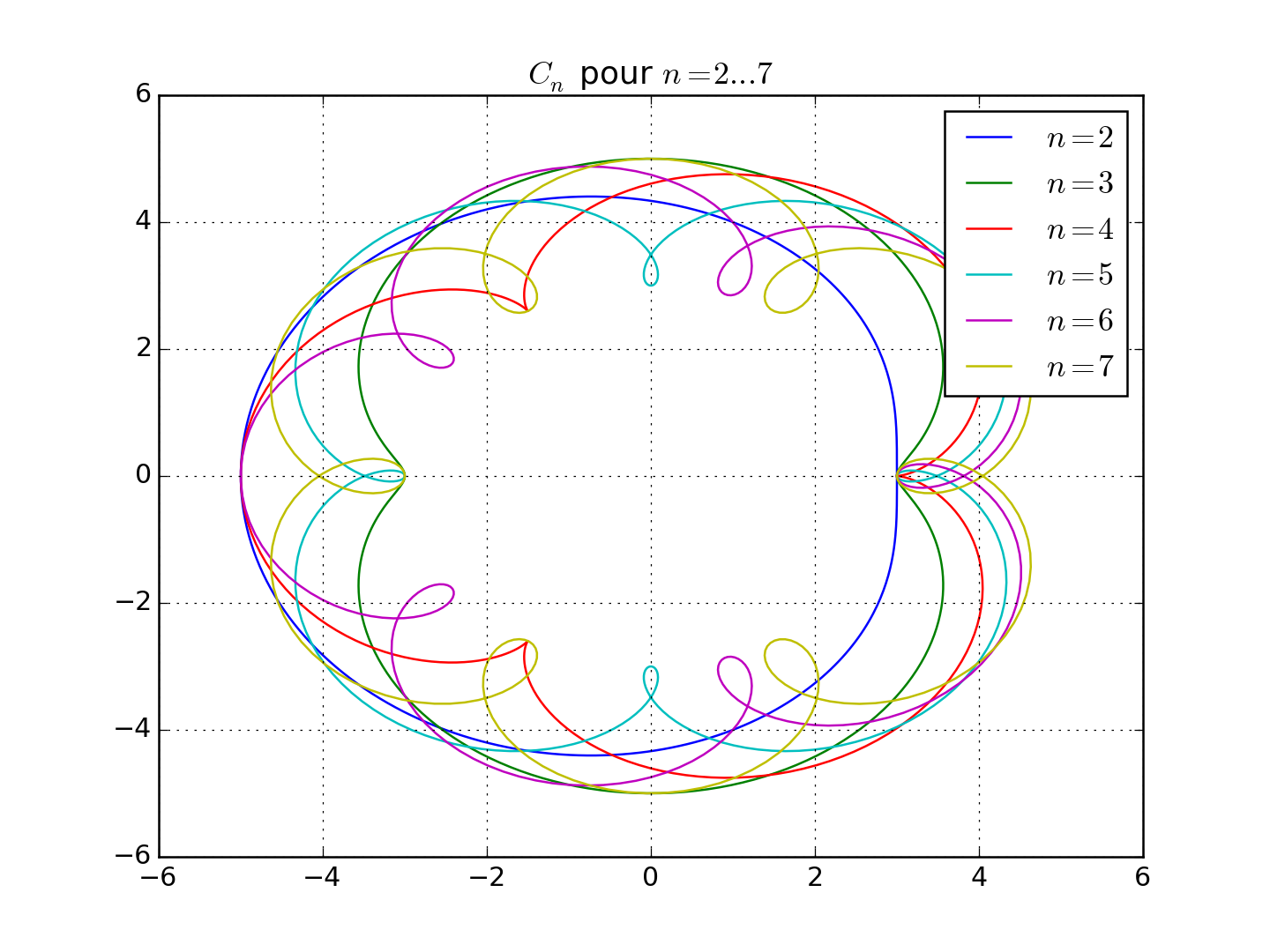
_images/PSI_Mat2_2015_24__figure1.png
PSI_Mat2_2015_24.q2()[source]

Question 2.

À l’aide de la figure, on observe les symétries suivantes :

  • symétrie par rapport à l’axe \(x\), car \(t \mapsto 4 \sin(t)\) et \(t \mapsto - \sin(n t)\) sont symétriques par rapport à \(\pi\),
  • pour \(n\) impaire (vert, cyan, doré sur notre figure 1), symétrie par rapport à l’axe \(y\), car \(t \mapsto 4 \cos(t)\) et \(t \mapsto - \cos(n t)\) sont symétriques par rapport à \(\pi\) si \(n\) est impaire (mais \(t \mapsto - \cos(n t)\) ne l’est pas si \(n\) est pair).
PSI_Mat2_2015_24.q3()[source]

Question 3.

À l’aide de la figure, on observe que seule la courbe rouge (\(n = 4\)) admet des points non-réguliers, et qu’elle en a trois, correspondant à \(t = 0, 2\pi/3, 4\pi/3\).

Il faudrait aussi prouver la même chose, faites le sur papier (c’est un bon exercice). Si besoin, cf. le chapitre 24.3.3 de ce cours de MPSI (§24.3.3 p692).

Les deux fonctions \(t \mapsto x_n(t)\) et \(t \mapsto y_n(t)\) sont de classes \(\mathcal{C}^{\infty}\), mais pour étudier les points non-réguliers (aussi appelés singuliers), il faut trouver les points où le vecteur vitesse \(v(t) = [x_n'(t), y_n'(t)]\) s’annule.

On calcule d’abord le vecteur vitesse :

\[v(t) = [x_n'(t), y_n'(t)] = [ -4 \sin(t) + n \sin(nt), +4 \cos(t) - n \cos(nt)].\]

On cherche à avoir \(n'(t) = 0\), soit \(4 \sin(t) = n \sin(n t)\) et \(4 \cos(t) = n \cos(n t)\).

En prenant la somme des carrés des deux côtés, on obtient d’abord que \(n'(t) = 0 \implies 4^2 = n^2 \implies n = 4\) : c’est déjà pas mal, on vient de prouver que seule la courbe \(n = 4\) peut avoir des points non-réguliers.

Désormais, pour \(n = 4\), \(n'(t) = 0\) ssi \(\sin(t) = \sin(4 t)\) et \(\cos(t) = \cos(4 t)\). On remarque déjà que les trois points observés, \(t = 0, 2\pi/3, 4\pi/3\), fonctionnent, mais on doit montrer que ce sont les seuls.

Si \(\sin(t) = \sin(4 t)\) et \(\cos(t) = \cos(4 t)\), alors en utilisant l’identité d’Euler, cela implique que \(\mathrm{e}^{it} = \mathrm{e}^{4it}\) qui implique que \(\mathrm{e}^{3it} = 1\), et donc \(3t = 0 \;\mathrm{mod}\; 2\pi\), or \(t \in [0, 2\pi]\), donc cela implique que \(t \in \{0, 2\pi/3, 4\pi/3\}\).

Et voilà.

PSI_Mat2_2015_24.l(n)[source]

Calcule la longueur \(l_n\) de façon approchée via la fonction scipy.integrate.quad() (quad(f, a, b)), appliquée à dOM_sur_dt() définie dans le corps de la fontion def l(n): ....

En effet, dOM_sur_dt() doit dépendre de n, mais scipy.integrate.quad() a besoin d’une fonction qui n’accepte qu’un seul paramètre : si f est \(t \mapsto f(t)\), alors quad(f, a, b) \(\simeq \int_{a}^{b} f(t) \; \mathrm{d}t\).

Note

En fait, scipy.integrate.quad() accepte une fonction du genre \(g : (t, n) \mapsto g(t, n)\) si on l’appelle comme quad(g, 0, 1, args=(8)) (qui sera une approximation de \(\int_{a = 0}^{b = 1} g(t, n = 8) \; \mathrm{d}t)\).

PSI_Mat2_2015_24.q4()[source]

Question 4.

Il faut se souvenir de la formule donnant la longueur d’un arc paramétré. Encore une fois, si besoin, cf. le chapitre 24.1 de ce cours de MPSI (§24.1 p680).

La formule a connaître est :

\[l_n = \int_{t = 0}^{t = 2\pi} \left\| \frac{\overrightarrow{OM}(t)}{\mathrm{d} t} \right\|_2 \mathrm{d} t.\]
  1. On définit une fonction dOM_sur_dt(t) qui calcule \(\left\| \frac{\overrightarrow{OM}(t)}{\mathrm{d} t} \right\|_2 = \sqrt{x_n'(t)^2 + y_n'(t)^2}\) (note : c’est une fonction exacte),
  2. On utilise ensuite la fonction scipy.integrate.quad() pour calculer l’intégrale de façon numérique,
  3. On met tout ça dans une fonction \(l(n)\) qui donnera la longueur de la courbe en fonction de n,
  4. On calcule la liste des valeurs de \(l(n)\) par une liste en compréhension, avec \(n = 1 .. 20\),
  5. On affiche ces valeurs (avec matplotlib.pyplot.plot()).

Cela donne une figure comme celle ci-dessous :

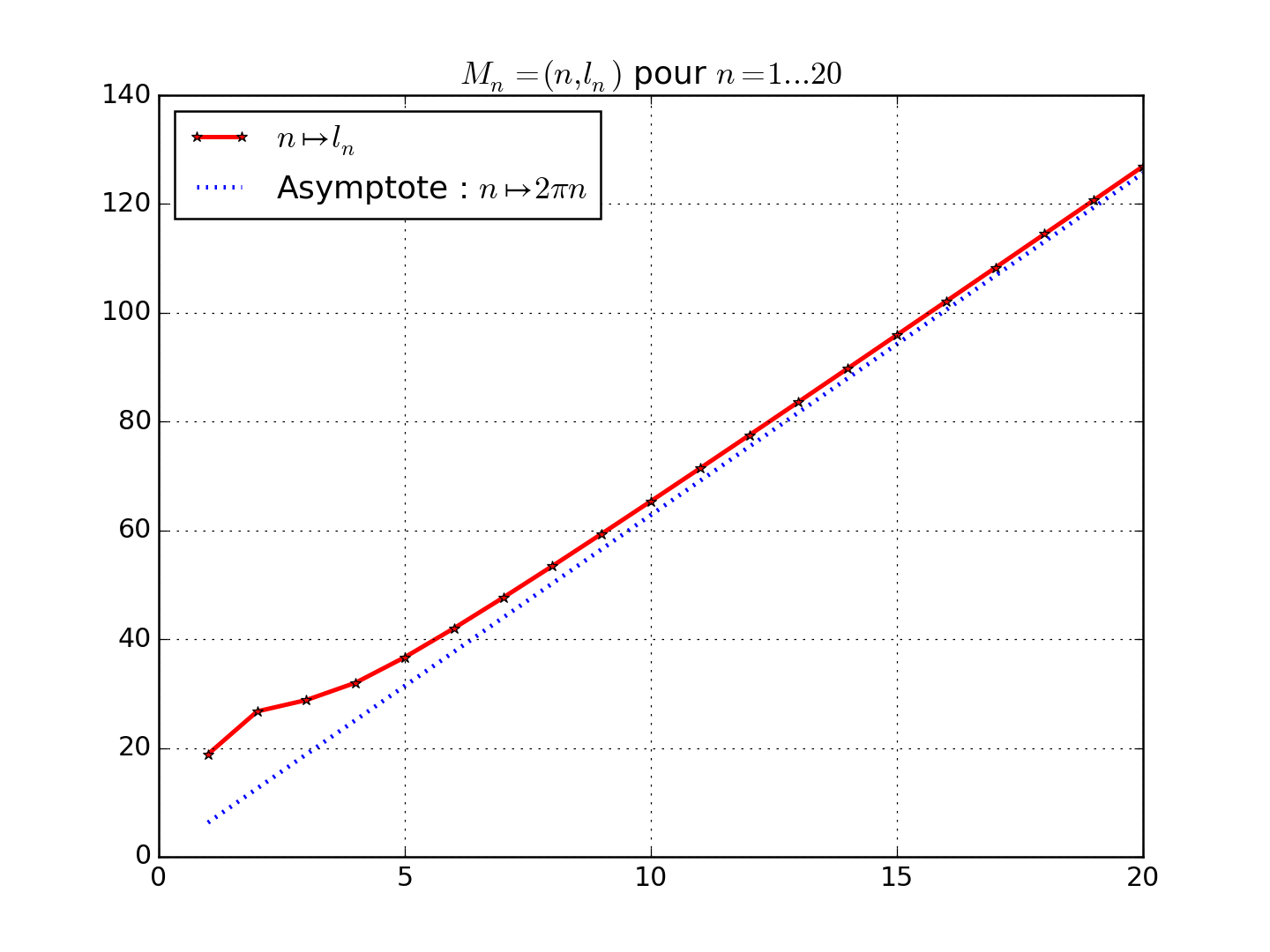
_images/PSI_Mat2_2015_24__figure2.png
PSI_Mat2_2015_24.q5()[source]

Question 5.

On s’inspire de la figure précédente pour deviner une forme que peut avoir \(l_n\) pour \(n \to +\infty\). Son comportement semble parfaitement linéaire... En lisant la figure précédente, on trouve \(l_n \simeq 2 \pi \times n\).

On calcule :

\[\begin{split}&\left\| \frac{\overrightarrow{OM}(t)}{\mathrm{d} t} \right\|_2 \\ &= \sqrt{x_n'(t)^2 + y_n'(t)^2} \\ &= \sqrt{(- 4 \sin(t) + n \sin(n t))^2 + (4 \cos(t) - n \cos(n t))^2}\end{split}\]

Donc pour \(n \to +\infty\), \(- 4 \sin(t) + n \sin(n t) = \mathcal{O}(n \sin(n t))\), \(4 \cos(t) - n \cos(n t) = \mathcal{O}(- n \cos(n t))\), puisque \(- 4 \sin(t), 4 \cos(t) \in [-4, 4]\) sont bornés.

Donc pour \(n \to +\infty\) :

\[\begin{split}\sqrt{((- 4 \sin(t) + n \sin(n t))^2 + (4 \cos(t) - n \cos(n t))^2} \\ \simeq \sqrt{n^2 \sin^2(n t) + n^2 \cos^2(n t)} \\ = n \sqrt{\sin^2(n t) + \cos^2(n t)} \\ = n.\end{split}\]

Ainsi, \(\int_{0}^{2\pi} \lim_{n\to\infty} \left\| \frac{\overrightarrow{OM}(t)}{\mathrm{d} t} \right\|_2 \mathrm{d}t = \int_{0}^{2\pi} n \mathrm{d}t = 2 \pi n\). Reste à justifier comment on peut inverser l’intégrale et la limite.

On se souvient du théorème de convergence dominée, et sur papier on ferait proprement un calcul justifiant qu’on a une borne uniforme qui convient (comme \(|4 \cos(t) - n \cos(nt)| \leq 4 + n\) et \(|- 4 \sin(t) + n \sin(nt)| \leq 4 + n\) c’est assez rapide).

Conclusion : \(l_n \simeq_{n \to \infty} 2 \pi n\).

Note

Au tableau et sur papier, vous devriez justifier mieux, surtout les \(\simeq\) et \(\mathcal{O}\). (J’ai juste la flemme.)

Sortie du script

$ python PSI_Mat2_2015_24.py
Test automatique de toutes les doctests ecrites dans la documentation (docstring) de chaque fonction :
Trying:
    import numpy as np
Expecting nothing
ok
Trying:
    import matplotlib.pyplot as plt
Expecting nothing
ok
Trying:
    from scipy.integrate import quad
Expecting nothing
ok
7 items had no tests:
    __main__
    __main__.l
    __main__.q1
    __main__.q2
    __main__.q3
    __main__.q4
    __main__.q5
1 items passed all tests:
   3 tests in __main__.q0
3 tests in 8 items.
3 passed and 0 failed.
Test passed.

Plus de details sur ces doctests peut etre trouve dans la documentation de Python:
https://docs.python.org/3/library/doctest.html (en anglais)

Le fichier Python se trouve ici : PSI_Mat2_2015_24.py.