PC_Mat2_2015_28 ¶

Thème : simulations probabilistes, développements limités, calcul asymptotique, calculs de sommes.

Documentation¶

Correction d’un exercice de maths avec Python, issu des annales pour les oraux du concours Centrale-Supélec.

Sujet : PC 2, http://www.concours-centrale-supelec.fr/CentraleSupelec/MultiY/C2015/PC-Mat2-2015-28.pdf
Dates : séances de révisions, vendredi 10 et samedi 11 juin (2016).
Auteur : Lilian Besson, pour le cours d’informatique pour tous en prépa MP au Lycée Lakanal (http://perso.crans.org/besson/infoMP/),
Licence : MIT Licence (http://lbesson.mit-license.org).

PC_Mat2_2015_28.q0()[source]¶

Préliminaires :

Comme pour tous ces exercices, on commence par importer les modules requis, ici numpy et matplotlib :

>>> import numpy as np
>>> import matplotlib.pyplot as plt

PC_Mat2_2015_28.q1()[source]¶

Question 1.

On commence par écrire une fonction pour calculer \({n \choose k}\), plusieurs approches sont possibles :

on écrit une fonction factorial() (de \(\mathbb{N} \to \mathbb{N}\)) qui calcule \(n!\), et on utilise \({n \choose k} = \frac{n!}{k! (n-k)!}\). Ça marche, mais ce sera assez lent, et très redondant en calculs (cf. binom_factorial()).
ou on écrit une fonction binom() directement, en se basant sur la propriété élémentaire \({n \choose k} = (\frac{n-k+1}{k}) {n \choose k-1}\).

C’est la deuxième approché, itérative et facile à écrire, que je recommande.

Note: on pense à l’optimisation gratuite qui consiste à remplacer \(k\) par \(\min(k, n-k)\).

Ça donne quelque chose comme ça :

def binom(n, k):
    if k < 0 or k > n:    # Cas de base (n k) = 0
        return 0
    if k == 0 or k == n:  # Cas de base (n k) = 1
        return 1
    k = min(k, n - k)     # Utilise la symétrie !
    produit = 1
    for i in range(k):
        produit *= (n - i)
    for i in range(k):
        produit //= (i + 1)
    return int(produit)   # Force à être entier !

Voir aussi

En fait, on peut aussi utiliser scipy.special.binom() du module scipy.special, qui fonctionne très bien (elle renvoit un flottant attention) :

>>> from scipy.special import binom as binom2
>>> binom2(10, 2)
45.0

PC_Mat2_2015_28.binom(n, k)[source]¶

Calcule efficacement en \(\mathcal{O}(\min(k, n-k))\) multiplication et division entières le nombre binom(n, k) \(= {n \choose k}\) (et en \(\mathcal{O}(1)\) en mémoire !).

Exemples :

>>> binom(6, -3)
0
>>> binom(6, 0)
1
>>> binom(6, 1)
6
>>> binom(6, 2)
15
>>> binom(6, 3)
20
>>> binom(6, 4)
15
>>> binom(6, 5)
6
>>> binom(6, 6)
1

PC_Mat2_2015_28.binom_factorial(n, k)[source]¶

Coefficient binomial calculé en utilisant des factorielles (via math.factorial()) :

Exemples :

>>> binom_factorial(6, 0)
1
>>> binom_factorial(6, 1)
6
>>> binom_factorial(6, 2)
15
>>> binom_factorial(6, 3)
20
>>> binom_factorial(6, 4)
15
>>> binom_factorial(6, 5)
6
>>> binom_factorial(6, 6)
1

PC_Mat2_2015_28.q2()[source]¶

Question 2.

Dès qu’on dispose d’une fonction binom(), comme demandé en Q1, on peut écrire très facilement la fonction Sn(), juste en écrivant sa définition :
```
def Sn(n):
    n_sur_2_plus_1 = (n // 2) + 1
    return sum((-1)**k * binom(n, 2*k) for k in range(0, n_sur_2_plus_1))
```
On a calculé n_sur_2_plus_1 1 + le plus grand entier k tel que \(2k \leq n\) (le 1 + vient de ce que range(debut, dernier) demande à avoir dernier = 1 + fin pour inclure fin).
Et on a utilisé range() pour obtenir la liste des \(k\) tels que \(0 \leq 2k \leq n\).

PC_Mat2_2015_28.Sn(n)[source]¶: Calcul naïf et rapide de \(S_n\) définie par :

\[S_n := \sum_{0 \leq 2k \leq n} (-1)^k {n \choose 2k}.\]

PC_Mat2_2015_28.Tn(n)[source]¶: Calcul naïf et rapide de \(T_n\) définie par :

\[T_n := 2^{\frac{n}{2}} \cos\left(n \frac{\pi}{4} \right).\]

PC_Mat2_2015_28.q3()[source]¶

Question 3.

On commence par écrire une fonction, très simple aussi, qui calcule \(T_n\), en utilisant au choix math.cos() ou numpy.cos(), et math.py ou numpy.py, pour calculer \(\cos\left(n \frac{\pi}{4}\right)\). Cf. Tn() :
```
def Tn(n):
    return 2.0 ** (n / 2) * np.cos(n * np.pi / 4)
```

Ensuite, on calcule les valeurs de \(S_n\) et \(T_n\) pour \(n = 0, \dots, 10\), avec Sn() et Tn() :

valeurs_n = list(range(0, 10 + 1))
valeurs_Sn = [ Sn(n) for n in valeurs_n ]
valeurs_Tn = [ Tn(n) for n in valeurs_n ]

Puis on les affiche, simplement avec matplotlib.pyplot.plot() (plt.plot) :

plt.figure()    # Nouvelle figure
plt.hold(True)  # Plusieurs graphiques sur la même figure
plt.plot(valeurs_n, valeurs_Sn, 'b+-', label='$S_n$')
plt.plot(valeurs_n, valeurs_Tn, 'r*-', label='$T_n$')
plt.title("Valeurs de $S_n$, $T_n$ pour $n = 0 ... 10$.")  # Ajoute un titre
plt.legend()  # Utilise les deux label='...' plus hauts
plt.show()  # On montre la figure.

Cela devrait donner une figure comme ça :

Et on constate que \(T_n\) et \(S_n\) sont égaux. C’est ce qu’on va montrer en Q6 ((1)).

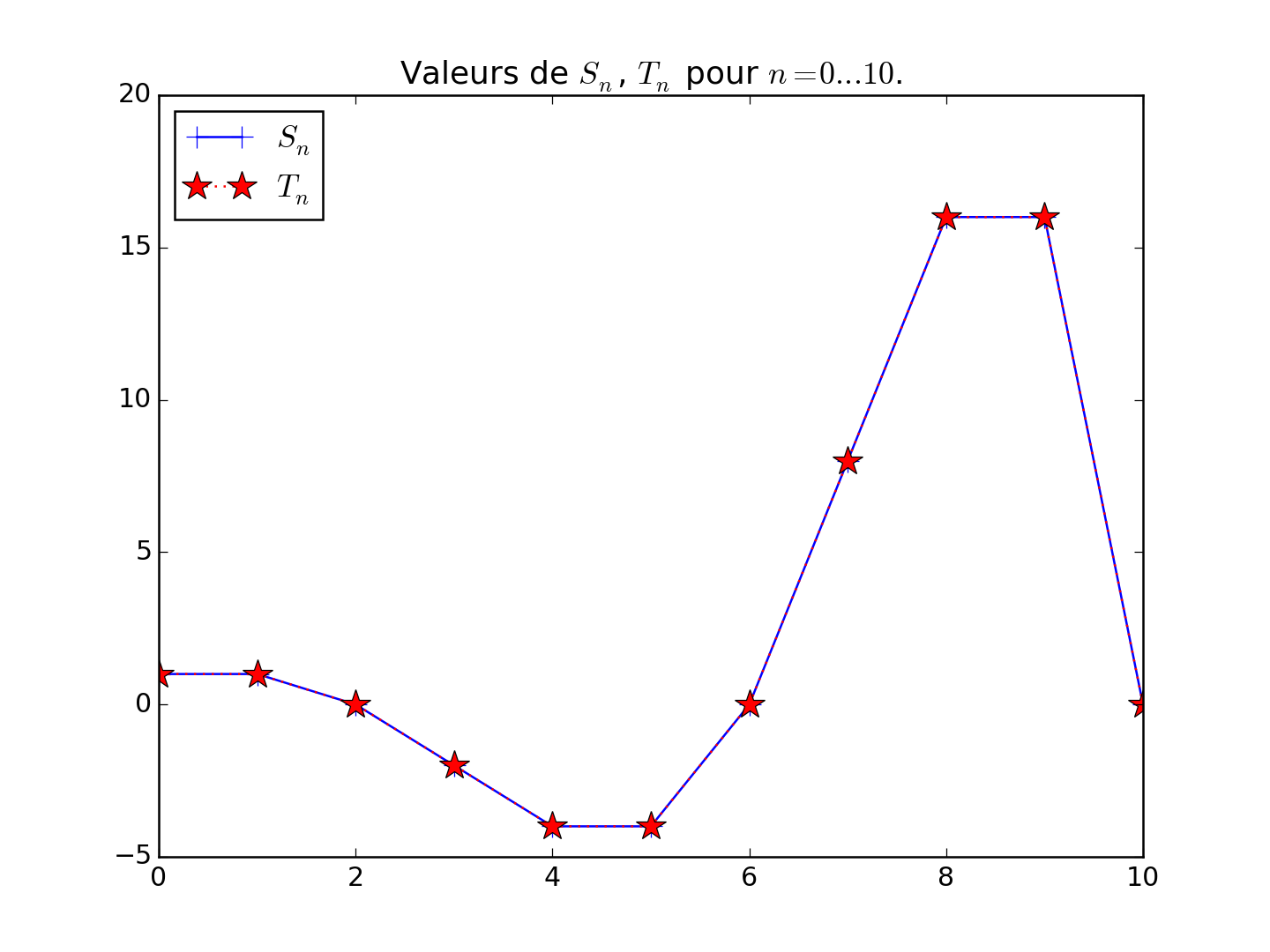
PC_Mat2_2015_28.q4()[source]¶

Question 4.

C’est du cours, ça vient du cours de maths et pas d’informatique.
Si besoin, n’hésitez pas à relire une fiche de rappels sur les développements entières (ou sur les développements limités).
On se souvient donc que \(\exp\) et \(\cos\) ont un développements en série entière, de rayons de convergence \(R = +\infty\), donnés par ces formules :

\[\begin{split}\exp(x) &= \sum_{k=0}^{+\infty} \frac{x^k}{k!}, \\ \cos(x) &= \sum_{k=0}^{+\infty} (-1)^{k} \frac{x^{2k}}{(2k)!}.\end{split}\]

Indice

Il est absolument VITAL de se souvenir de la formule pour \(\exp(x)\), puisqu’elle permet de retrouver plein d’autres développements :

\(\cosh\) est la partie paire de \(\exp\), donc \(\cosh(x) = \sum\limits_{k=0}^{+\infty} \frac{x^{2k}}{(2k)!}\) en gardant les puissances paires,
\(\sinh\) est la partie impaire de \(\exp\), donc \(\sinh(x) = \sum\limits_{k=0}^{+\infty} \frac{x^{2k+1}}{(2k+1)!}\) en gardant les puissances impaires,
\(\cos\) est la partie réelle de \(x\mapsto\exp(ix)\), donc \(\cos(x) = \sum\limits_{k=0}^{+\infty} \frac{(ix)^{2k}}{(2k)!} = \sum\limits_{k=0}^{+\infty} (-1)^k \frac{x^{2k}}{(2k)!}\) en gardant les puissances paires,
\(\sin\) est la partie imaginaire de \(x\mapsto\exp(ix)\), donc \(\sin(x) = \frac{1}{i} \sum\limits_{k=0}^{+\infty} \frac{(ix)^{2k+1}}{(2k)!} = \sum\limits_{k=0}^{+\infty} (-1)^k \frac{x^{2k+1}}{(2k)!}\) en gardant les puissances impaires.

PC_Mat2_2015_28.q5()[source]¶

Question 5.

C’est aussi du cours, on prend le produit \(x \mapsto \cos(x) \mathrm{e}^x\) de deux fonctions \(\cos\) et \(\exp\) développables en séries entières, toutes les deux de rayon \(R = +\infty\).
Donc la fonction produit est aussi développable en S.E. et de rayon aussi \(R = +\infty\) (c’est le cas le plus simple du théorème du produit de Cauchy).

Attention

Le sujet ne demandait PAS de donner ici le développement de \(x \mapsto \cos(x) \mathrm{e}^x\), mais ce sera requis à la question suivante...

PC_Mat2_2015_28.q6()[source]¶

Question 6.

Question purement mathématique, mais elle n’est vraiment pas facile.
J’ai tenté au brouillon un bon moment, et tous les élèves présents au TP ont aussi essayé, sans succès.
En fait, ça a l’air assez dur. Nous n’avons pas réussi en TD avec toute la classe. Si vous avez une idée, contactez-moi svp.

PC_Mat2_2015_28.q7()[source]¶

Question 7.

Ici, le sujet demandait de prouver la même chose qu’à la question précédente, mais sans faire appel aux séries entières, et surtout, sans indication.
Il faut savoir être inventif, ou passer à la question suivante si on a aucune idée d’approche.
La démonstration est faite à la question suivante Q8 ci-dessous.

PC_Mat2_2015_28.q8()[source]¶

Question 8.

On commence par appliquer, pour un \(n \geq 1\), le binôme de Newton à \((1 + i)^n\) donne :

\[\begin{split}(1 + i)^n &= \sum_{k=0}^{n} 1^{n-k} i^k {n \choose k} \\ &= \sum_{k=0}^{n} i^k {n \choose k} \\ &= \sum_{0 \leq 2k \leq n} (-1)^k {n \choose 2k} + i \sum_{0 \leq 2k+1 \leq n} (-1)^k {n \choose 2k+1}.\end{split}\]

Donc \(S_n = \mathcal{R}\mathrm{eal}((1+i)^n)\), et cette deuxième somme \(U_n := \sum\limits_{0 \leq 2k+1 \leq n} (-1)^k {n \choose 2k+1} = \mathcal{I}\mathrm{mag}((1+i)^n)\).
Mais on peut aussi écrire \((1+i)\) en forme polaire, à savoir un module \(= \sqrt{2}\) et une phase \(= \frac{\pi}{4}\) :

\[(1+i) = \sqrt{2} \mathrm{e}^{i \frac{\pi}{4}}\]

Donc \((1+i)^n = \sqrt{2}^n \mathrm{e}^{i n \frac{\pi}{4}}\), ce qui prouve directement le résultat demandé en Q7 et ici en Q8 :

(1)¶\[\begin{split}S_n &= \sum_{0 \leq 2k \leq n} (-1)^k {n \choose 2k} &= 2^{\frac{n}{2}} \cos(n \frac{\pi}{4}) \\ U_n &= \sum_{0 \leq 2k+1 \leq n} (-1)^k {n \choose 2k+1} &= 2^{\frac{n}{2}} \sin(n \frac{\pi}{4}).\end{split}\]

Le sujet demandait qu’on vérifie cette dernière formule pour \(U_n\) par simulation, on fait donc exactement la même chose qu’aux questions Q2 et Q3 :

def Un(n):
    n_moins_1_sur_2_plus_1 = ((n - 1) // 2) + 1
    return sum((-1)**k * binom(n, 2*k+1) for k in range(1, n_sur_2_plus_1))

Et une deuxième fonction, pour calculer \(V_n := 2^{\frac{n}{2}} \sin(n \frac{\pi}{4})\) :

def Vn(n):
    return (np.sqrt(2) ** float(n)) * np.sin(n * np.pi / 4.0)

Ensuite, on calcule les valeurs de \(U_n\) et \(V_n\) pour \(n = 0, \dots, 10\), avec Un() et Tn() :

valeurs_n = list(range(0, 10 + 1))
valeurs_Un = [ Un(n) for n in valeurs_n ]
valeurs_Vn = [ Vn(n) for n in valeurs_n ]

Puis on les affiche, simplement avec matplotlib.pyplot.plot() (plt.plot), comme en Q3.
Cela devrait donner une figure comme ça :

Et on constate que \(U_n\) et \(V_n\) sont égaux. C’est ce qu’on a montré juste avant en Q8 ((1)).

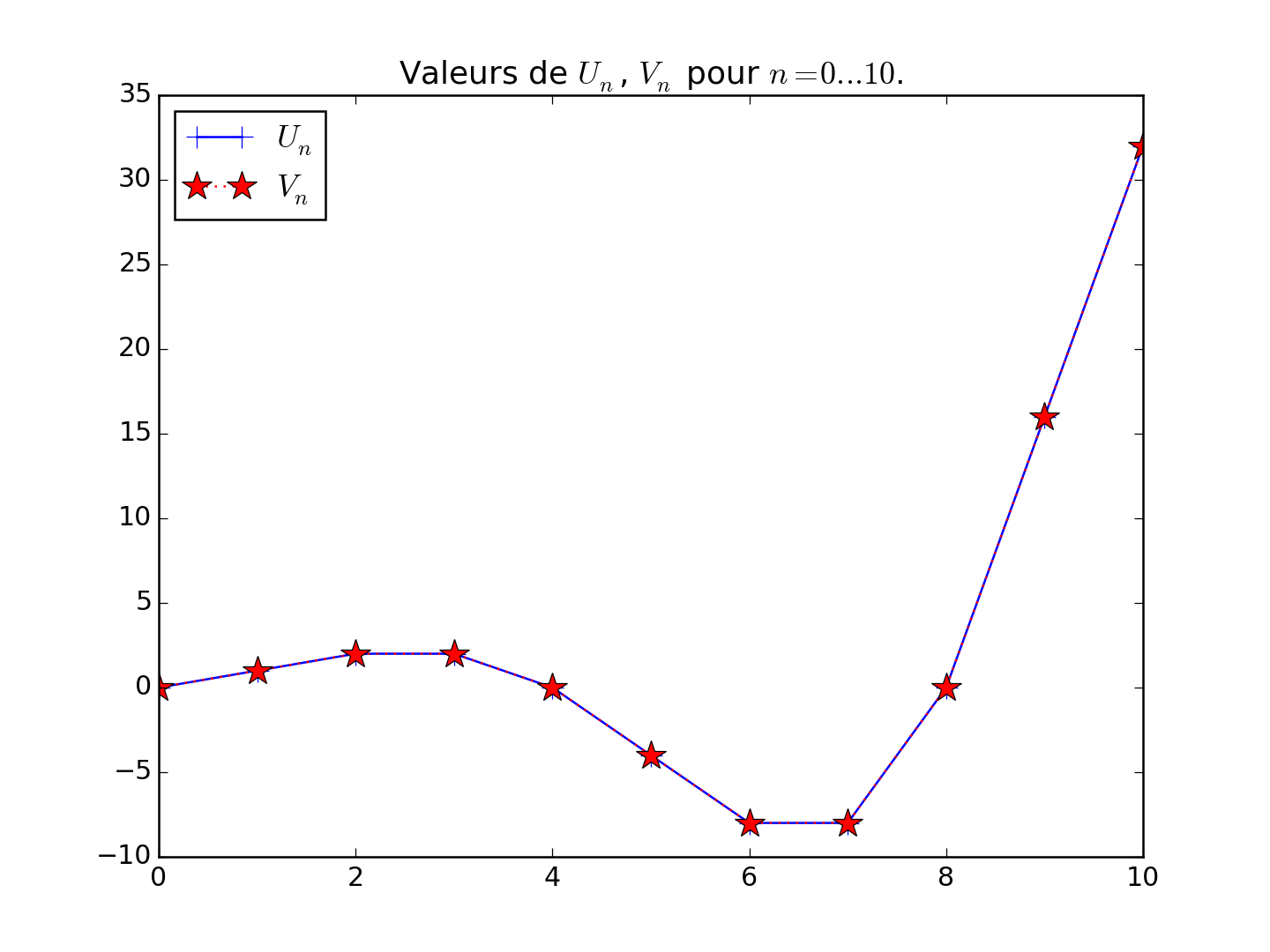
PC_Mat2_2015_28.Un(n)[source]¶: Calcul naïf et rapide de \(U_n\) définie par :

\[U_n := \sum_{0 \leq 2k+1 \leq n} (-1)^k {n \choose 2k+1}.\]

Indice

On a calculé n_moins_1_sur_2_plus_1 1 + le plus grand entier k tel que \(2k+1 \leq n\), par n_moins_1_sur_2_plus_1 = ((n - 1) // 2) + 1 (le 1 + vient de ce que range(debut, dernier) demande à avoir dernier = 1 + fin pour inclure fin).

PC_Mat2_2015_28.Vn(n)[source]¶: Calcul naïf et rapide de \(V_n\) définie par :

\[V_n := 2^{\frac{n}{2}} \sin\left(n \frac{\pi}{4} \right).\]

Sortie du script¶

$ python PC_Mat2_2015_28.py
Test automatique de toutes les doctests ecrites dans la documentation (docstring) de chaque fonction :
Trying:
    binom(6, -3)
Expecting:
    0
ok
Trying:
    binom(6, 0)
Expecting:
    1
ok
Trying:
    binom(6, 1)
Expecting:
    6
ok
Trying:
    binom(6, 2)
Expecting:
    15
ok
Trying:
    binom(6, 3)
Expecting:
    20
ok
Trying:
    binom(6, 4)
Expecting:
    15
ok
Trying:
    binom(6, 5)
Expecting:
    6
ok
Trying:
    binom(6, 6)
Expecting:
    1
ok
Trying:
    binom_factorial(6, 0)
Expecting:
    1
ok
Trying:
    binom_factorial(6, 1)
Expecting:
    6
ok
Trying:
    binom_factorial(6, 2)
Expecting:
    15
ok
Trying:
    binom_factorial(6, 3)
Expecting:
    20
ok
Trying:
    binom_factorial(6, 4)
Expecting:
    15
ok
Trying:
    binom_factorial(6, 5)
Expecting:
    6
ok
Trying:
    binom_factorial(6, 6)
Expecting:
    1
ok
Trying:
    import numpy as np
Expecting nothing
ok
Trying:
    import matplotlib.pyplot as plt
Expecting nothing
ok
Trying:
    from scipy.special import binom as binom2
Expecting nothing
ok
Trying:
    binom2(10, 2)
Expecting:
    45.0
ok
12 items had no tests:
    __main__
    __main__.Sn
    __main__.Tn
    __main__.Un
    __main__.Vn
    __main__.q2
    __main__.q3
    __main__.q4
    __main__.q5
    __main__.q6
    __main__.q7
    __main__.q8
4 items passed all tests:
   8 tests in __main__.binom
   7 tests in __main__.binom_factorial
   2 tests in __main__.q0
   2 tests in __main__.q1
19 tests in 16 items.
19 passed and 0 failed.
Test passed.

Plus de details sur ces doctests peut etre trouve dans la documentation de Python:
https://docs.python.org/3/library/doctest.html (en anglais)

Le fichier Python se trouve ici : PC_Mat2_2015_28.py.

PC_Mat2_2015_28¶

Documentation¶

Sortie du script¶

PC_Mat2_2015_28 ¶