PC_Mat2_2015_27

  • Thème : simulations probabilistes, calcul asymptotique.

Documentation

Correction d’un exercice de maths avec Python, issu des annales pour les oraux du concours Centrale-Supélec.

PC_Mat2_2015_27.q0()[source]

Préliminaires :

  • Comme pour tous ces exercices, on commence par importer les modules requis, ici uniquement matplotlib (pour la question Q5) :
>>> import matplotlib.pyplot as plt
PC_Mat2_2015_27.q1()[source]

Question 1.

Question purement mathématique.

  • Les variables aléatoires \(X_n\) suivent toutes une loi de Bernoulli de paramètre \(p = \frac{1}{2}\) (\(X_n \thicksim \mathcal{B}(\frac{1}{2})\)), et sont indépendantes,
  • Et la variable aléatoire \(S_n = \sum_{i=1}^{n} X_i\) suit donc une loi binomiale de paramètres \((n, p)\), par définition (\(S_n \thicksim \mathcal{Bin}(n, p)\).
  • Donc on peut utiliser le cours directement :
\[\begin{split}\mathbb{E}(S_n) = n \mathbb{E}(X_1) = n p = n \frac{1}{2} = \frac{n}{2}, \\ \mathbb{V}(S_n) = n \mathbb{V}(X_1) = n p (1-p) = n \frac{1}{4} = \frac{n}{4}.\end{split}\]
PC_Mat2_2015_27.q2()[source]

Question 2.

  • On va noter \(f(n)\) la fonction définie par \(\lfloor \frac{n}{2} \rfloor\) si \(n\) est impair (si \(n = 2 k + 1\), \(f(n) = k\)), et \(\lfloor \frac{n-1}{2} \rfloor = \frac{n}{2} - 1\) si \(n\) est pair (si \(n = 2 k\), \(f(n) = k - 1\)),
  • \(f : \mathbb{N}^{*} \to \mathbb{N}\) est bien définie, et vérifie \(\forall n > 0, f(n) = \min {i \in \mathbb{N} : i < \frac{n}{2}}\).
  • En fait, \(f(n) = \lfloor \frac{n-1}{2} \rfloor\) comme me l’avait fait remarqué un élève.
  • Ainsi, comme \(S_n\) est à support discret dans \([0, n] \cap \mathbb{N}\), on peut écrire \(\mathbb{P}(S_n < \frac{n}{2})\) comme une somme finie :
\[\begin{split}\mathbb{P}(S_n < \frac{n}{2}) &= \sum_{i = 0}^{i < \frac{n}{2}} \mathbb{P}(S_n = i) \\ &= \sum_{i = 0}^{f(n)} \mathbb{P}(S_n = i) \\ &= \sum_{i = 0}^{f(n)} {n \choose k} p^{k} (1-p)^{n - k} \\ &= \sum_{i = 0}^{f(n)} {n \choose k} (\frac{1}{2})^{k} (\frac{1}{2})^{n - k} \\ &= (\frac{1}{2})^{n} \sum_{i = 0}^{f(n)} {n \choose k}.\end{split}\]
  • Cette dernière expression semble satisfaisante : c’est une expression sommatoire explicite, et l’énoncé demandait de ne pas chercher à la simplifier.
PC_Mat2_2015_27.q3()[source]

Question 3.

Ici, pour écrire une fonction pour calculer \({n \choose k}\), plusieurs approches sont possibles :

  1. on écrit une fonction factorial() (de \(\mathbb{N} \to \mathbb{N}\)) qui calcule \(n!\), et on utilise \({n \choose k} = \frac{n!}{k! (n-k)!}\). Ça marche, mais ce sera assez lent, et très redondant en calculs (cf. binom_factorial()).
  2. ou on écrit une fonction binom() directement, en se basant sur la propriété élémentaire \({n \choose k} = (\frac{n-k+1}{k}) {n \choose k-1}\).

C’est la deuxième approché, itérative et facile à écrire, que je recommande.

  • Note: on pense à l’optimisation gratuite qui consiste à remplacer \(k\) par \(\min(k, n-k)\).

Ça donne quelque chose comme ça :

def binom(n, k):
    if k < 0 or k > n:    # Cas de base (n k) = 0
        return 0
    if k == 0 or k == n:  # Cas de base (n k) = 1
        return 1
    k = min(k, n - k)     # Utilise la symétrie !
    produit = 1
    for i in range(k):
        produit *= (n - i)
    for i in range(k):
        produit //= (i + 1)
    return int(produit)   # Force à être entier !

Voir aussi

En fait, on peut aussi utiliser scipy.special.binom() du module scipy.special, qui fonctionne très bien (elle renvoit un flottant attention) :

>>> from scipy.special import binom as binom2
>>> binom2(10, 2)
45.0
PC_Mat2_2015_27.binom(n, k)[source]

Calcule efficacement en \(\mathcal{O}(\min(k, n-k))\) multiplication et division entières le nombre binom(n, k) \(= {n \choose k}\) (et en \(\mathcal{O}(1)\) en mémoire !).

  • Exemples :
>>> binom(6, -3)
0
>>> binom(6, 0)
1
>>> binom(6, 1)
6
>>> binom(6, 2)
15
>>> binom(6, 3)
20
>>> binom(6, 4)
15
>>> binom(6, 5)
6
>>> binom(6, 6)
1
PC_Mat2_2015_27.binom_factorial(n, k)[source]

Coefficient binomial calculé en utilisant des factorielles (via math.factorial()) :

PC_Mat2_2015_27.q4()[source]

Question 4.

  • La question 2 donne la formule, cf. Q2,

  • Et la question précédente donne une fonction pour calcul \({n \choose k}\), binom(),

  • Il s’agit donc juste de combiner les deux :

    def sn2(n):
    n2 = ((n - 1) // 2)  # f(n)
    somme = sum(binom(n, k) for k in range(1, n2 + 1))
    return somme / 2**n

Indice

Pour éviter des problèmes de conversions entre entiers (int, en précision arbitraire) et flottants (float, en précision à 16 chiffres), il vaut mieux calculer somme / 2**n (division entre deux gros entiers) que (1/2)**n * somme (petit flottant fois gros entier... = 0 !).

PC_Mat2_2015_27.sn2(n)[source]

Calcule la formule obtenue en Q2, en sommant les valeurs de \({n \choose k}\) pour \(k = 1, \dots, f(n)\) (en utilisant binom()).

  • Exemples :
>>> sn2(1)
0.0
>>> sn2(2)
0.0
>>> sn2(3)
0.375
>>> sn2(4)
0.25
>>> sn2(5)
0.46875
>>> sn2(50)  
0.44386...
>>> sn2(500)  
0.48216...
>>> sn2(1000)  
0.48738...
>>> sn2(2000)  # Ca commence à prendre du temps  
0.49108...
PC_Mat2_2015_27.q5()[source]

Question 5.

  • Avec Q4, on dispose de la fonction sn2(), et donc on peut calculer \(u_{20k} =\) sn2(20k), très facilement.

  • On crée une liste de valeurs de \(u_{20k}\) pour \(k = 1,\dots,100\),

  • Enfin, on utilise simplement la fonction matplotlib.pyplot.plot() (plt.plot(X, Y)) pour afficher ces points :

    # On créé deux listes
valeurs_k = [ 20 * k for k in range(1, 100 + 1) ]
valeurs_u = [ sn2(k) for k in valeurs_k ]
plt.figure()  # Nouvelle figure
plt.plot(valeurs_k, valeurs_u)  # On affiche les points (k, sn2(20*k))
plt.title("Valeurs de u(20k) pour k = 1 .. 100")
plt.show()    # On affiche la figure

  • Cela devrait donner une figure comme ça :

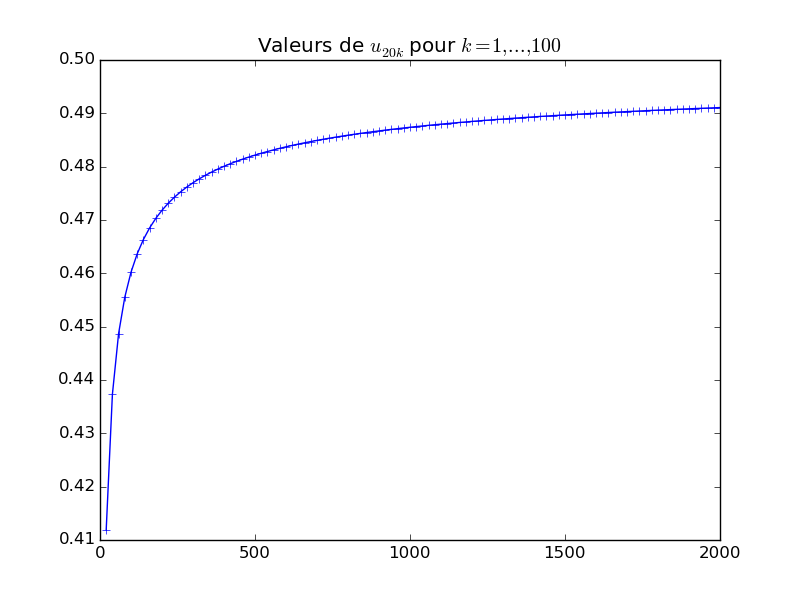
_images/PC_Mat2_2015_27__figure1.png
  • On peut donc raisonnablement conjecturer que la suite converge vers \(\frac{1}{2}\), ce qu’on va monter en Q7 et Q8 (de deux façons différentes), mais la convergence semble très lente.
PC_Mat2_2015_27.q6()[source]

Question 6.

  • Par symétrie, on obtient directement que \(\mathbb{P}(S > \frac{n}{2}) = \mathbb{P}(S < \frac{n}{2}) = u_n\).
  • Soit \(n \geq 1\). De façon immédiate, on peut décomposer l’intervalle entier \([0, n] \cap \mathbb{N}\) en trois morceaux disjoints :
\[\begin{split}[0, n] \cap \mathbb{N} &= { i \in \mathbb{N} : 0 \leq i \leq n} \\ &= \{ 0 \leq i < \frac{n}{2} \} \cup \{ i = \frac{n}{2} \} \cup \{ \frac{n}{2} < i \leq n \}.\end{split}\]
  • Donc en considérant les probabilités pour la v.a. \(S_n\), on a directement (par la formule de l’union, cas disjoint) :
\[\begin{split}1 &= \mathbb{P}(S \in [0, n] \cap \mathbb{N}) \\ &= \mathbb{P}(S \in \{ 0 \leq i < \frac{n}{2} \} \cup \{ i = \frac{n}{2} \} \cup \{ \frac{n}{2} < i \leq n \}) \\ &= \mathbb{P}(S \in \{ 0 \leq i < \frac{n}{2} \}) + \mathbb{P}(S \in \{ i = \frac{n}{2} \}) + \mathbb{P}(S \in \{ \frac{n}{2} < i \leq n \}) \\ &= \mathbb{P}(S < \frac{n}{2}) + \mathbb{P}(S_n = \frac{n}{2}) + \mathbb{P}(S > \frac{n}{2}) \\ &= u_n + \mathbb{P}(S_n = \frac{n}{2}) + \mathbb{P}(S > \frac{n}{2}).\end{split}\]
  • Et de même, on procède pareil pour montrer, trivialement, que :
\[\begin{split}v_n &= \mathbb{P}(S \geq \frac{n}{2}) \\ &= \mathbb{P}(S_n = \frac{n}{2}) + \mathbb{P}(S > \frac{n}{2}) \\ &= \mathbb{P}(S_n = \frac{n}{2}) + \mathbb{P}(S < \frac{n}{2}) \\ &= \mathbb{P}(S_n = \frac{n}{2}) + u_n.\end{split}\]
  • Conclusion : on a bien montré que \(\forall n \geq 1, v_n = u_n + \mathbb{P}(S_n = \frac{n}{2})\).
PC_Mat2_2015_27.q7()[source]

Question 7.

  • D’après les calculs faits en Q6, \(u_n \to \frac{1}{2}\) ssi \(\mathbb{P}(S_n = \frac{n}{2}) \to 0\) pour \(n \to +\infty\).
  • Mais, pour \(n\) impair, on a déjà que \(\frac{n}{2} \not\in \mathbb{N}\) donc \(\mathbb{P}(S_n = \frac{n}{2}) = 0\).
  • Et pour \(n = 2k\) pair, on peut écrire exactement la valeur de \(\mathbb{P}(S_n = \frac{n}{2}) = \mathbb{P}(S_n = k) = (\frac{1}{2})^n {n \choose k}\).
  • On étudie la limite de \(\frac{1}{4^k}{2k \choose k}\), et sans même avoir besoin d’un équivalent (ie. formule de Stirling) on devrait (sa)voir que ça tend vers \(0\). Mais soyons rigoureux :

Note

Preuve : (avec Stirling). On a :

\[\begin{split}{2k \choose k} &= \frac{(2k)!}{(k!)^2} \\ &\thicksim \frac{\sqrt{2 \pi 2k}(\frac{2k}{\mathrm{e}})^{2k}}{(\sqrt{2 \pi k}(\frac{k}{\mathrm{e}})^{k})^2} \\ &\thicksim \frac{2\sqrt{\pi k} 2^{2k} (\frac{k}{\mathrm{e}})^{2k}}{2 \pi k(\frac{k}{\mathrm{e}})^{2k}} \\ &\thicksim \frac{\sqrt{\pi k} 4^k}{\pi k} \\ &\thicksim \frac{4^k}{\sqrt{\pi k}}.\end{split}\]

Et donc \(\frac{1}{4^k}{2k \choose k} \thicksim \frac{1}{\sqrt{\pi k}}\) pour \(k \to +\infty\), ce qui prouve que \(\mathbb{P}(S_{2k} = \frac{2k}{2}) \to 0\) aussi.

  • Conclusion : que \(n\) soit pair ou impair, on a bien montré que \(\mathbb{P}(S_n = \frac{n}{2}) \to 0\) pour \(n \to +\infty\).
  • Et donc, cela prouve le résultat observé empiriquement en Q5 :
\[\lim_{n \to +\infty} u_n = \frac{1}{2}.\]

Note

On a une estimation de la vitesse de convergence de \(\mathbb{P}(S_n = \frac{n}{2})\) vers \(0\) (en \(\mathcal{O}(\frac{1}{\sqrt{n}}\)), donc cela donne directement un ordre de grandeur de convergence de \(u_n\) vers sa limite !

Cool non ? En fait, c’est une conséquence immédiate du théorème central limite, qui est LE résultat central en statistiques (cf. ce point là).

PC_Mat2_2015_27.q8()[source]

Question 8.

Indice

On remarque que l’énoncé nous aide en suggérant ici de se restreindre aux \(n\) pairs, ce qui est exactement ce qu’on a fait en Q7.

  • De même qu’au dessus, on obtient que :
\[w_n := \mathbb{P}(S_{2n} = n) = \frac{1}{4^n}{2n \choose n}\]
  • Donc on peut calculer explicitement \(\ln(\frac{w_{n+1}}{w_n})\) :
\[\begin{split}\ln(\frac{w_{n+1}}{w_n}) &= \ln( \frac{1}{4} {2(n+1) \choose (n+1)}/{2n \choose n} ) \\ &= - \ln(4) + \ln( \frac{(2(n+1))!}{((n+1)!)^2} / \frac{(2n)!}{(n!)^2} ) \\ &= - \ln(4) + \ln( \frac{(2n+2)(2n+1)}{(n+1)^2} ) \\ &= - 2\ln(2) + \ln( 2\frac{2n+1}{n+1} ) \\ &= - 2\ln(2) + \ln(2) + \ln(\frac{2n+1}{n+1}) \\ &= - \ln(2) + \ln(\frac{(2n+1)}{n+1}) \\ &= \ln(\frac{(2n+1)}{2(n+1)}) \\ &= -\ln(\frac{2n+2}{2n+1}) = -\ln(\frac{(2n+1) + 1}{2n+1}) \\ &= -\ln(1 + \frac{1}{2n+1}).\end{split}\]
  • Ensuite, en notant \(x = \frac{1}{2n+1}\), \(x \to 0\) si \(n \to \infty\), et comme \(\ln(1 + x) \thicksim x\), on obtient :
\[\begin{split}\ln(\frac{w_{n+1}}{w_n}) &= -\ln(1 + \frac{1}{2n+1}) \\ &\thicksim - \frac{1}{2n+1} \to 0.\end{split}\]
  • Dès lors, on peut sommer la série de terme général \(\ln(\frac{w_{n+1}}{w_n})\), pour obtenir, par comparaison avec la série divergente de terme général de signe constant (négatif) \(- \frac{1}{2n+1}\), une série divergente vers \(-\infty\).
  • Mais on reconnaît une somme téléscopique : \(\sum_{n=0}^{N} \ln(\frac{w_{n+1}}{w_n}) = \ln(w_{N+1}) - \ln(w_{0})\), donc ça montre que \(\ln(w_{N+1}) \to -\infty\) pour \(N \to +\infty\).
  • Ainsi on obtient directement que \(w_n \to 0\) pour \(n \to +\infty\), c’est ce qui était demandé.
  • Enfin on obtient comme voulu que \(u_n \to \frac{1}{2}\).

Note

Ici aussi, cet équivalent \(\ln(\frac{w_{n+1}}{w_n}) \thicksim - \frac{1}{2n+1}\) donne une indication sur la vitesse de convergence de \(w_n \to 0\) (en \(\mathcal{O}(\sqrt{n})\)), qui est la même que celle obtenue en Q7. Cool.

Sortie du script

$ python PC_Mat2_2015_27.py
Test automatique de toutes les doctests ecrites dans la documentation (docstring) de chaque fonction :
Trying:
    binom(6, -3)
Expecting:
    0
ok
Trying:
    binom(6, 0)
Expecting:
    1
ok
Trying:
    binom(6, 1)
Expecting:
    6
ok
Trying:
    binom(6, 2)
Expecting:
    15
ok
Trying:
    binom(6, 3)
Expecting:
    20
ok
Trying:
    binom(6, 4)
Expecting:
    15
ok
Trying:
    binom(6, 5)
Expecting:
    6
ok
Trying:
    binom(6, 6)
Expecting:
    1
ok
Trying:
    import matplotlib.pyplot as plt
Expecting nothing
ok
Trying:
    from scipy.special import binom as binom2
Expecting nothing
ok
Trying:
    binom2(10, 2)
Expecting:
    45.0
ok
Trying:
    sn2(1)
Expecting:
    0.0
ok
Trying:
    sn2(2)
Expecting:
    0.0
ok
Trying:
    sn2(3)
Expecting:
    0.375
ok
Trying:
    sn2(4)
Expecting:
    0.25
ok
Trying:
    sn2(5)
Expecting:
    0.46875
ok
Trying:
    sn2(50)  # doctest: +ELLIPSIS
Expecting:
    0.44386...
ok
Trying:
    sn2(500)  # doctest: +ELLIPSIS
Expecting:
    0.48216...
ok
Trying:
    sn2(1000)  # doctest: +ELLIPSIS
Expecting:
    0.48738...
ok
Trying:
    sn2(2000)  # Ca commence à prendre du temps  # doctest: +ELLIPSIS
Expecting:
    0.49108...
ok
9 items had no tests:
    __main__
    __main__.binom_factorial
    __main__.q1
    __main__.q2
    __main__.q4
    __main__.q5
    __main__.q6
    __main__.q7
    __main__.q8
4 items passed all tests:
   8 tests in __main__.binom
   1 tests in __main__.q0
   2 tests in __main__.q3
   9 tests in __main__.sn2
20 tests in 13 items.
20 passed and 0 failed.
Test passed.

Plus de details sur ces doctests peut etre trouve dans la documentation de Python:
https://docs.python.org/3/library/doctest.html (en anglais)

Le fichier Python se trouve ici : PC_Mat2_2015_27.py.