


suivant: Calcul de la base
monter: Contrôle de la qualité
précédent: Bibliographie
Table des matières
Calcul des coordonnées des points de Gauss
Afin de calculer l'erreur par élément, il sera nécessaire de calculer des intégrales numériques. Il est cependant impossible de calculer celles-ci formellement, car le programme de calcul d'erreur est réalisé en langage Fortran. S'il avait été réalisé dans un langage tel que le language de programmation de Matlab ou Maple, il aurait peut-être été possible de les calculer exactement. On a donc choisi d'utiliser une méthode d'intégration numérique de Gauss (le nombre de points par élément sera défini plus loin) pour les carrés, et une méthode de Hammer pour les éléments triangulaires.
La méthode de calcul des coordonnées de ces points tient compte de
l'isoparamétrie : En effet, on connaît les coordonnées des points
de Gauss dans l'élément de référence ; l'isoparamétrie permet
ensuite de calculer les coordonnées réelles de ces points.
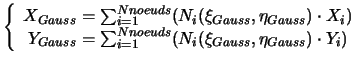 |
|
|
(A.1) |
Il suffit alors de répéter cette opération pour tous les éléments.
Cependant, il existe plusieurs ordres de calcul, avec pour certains de forts inconvénients :
Cela revient à poser la question : Vaut-il mieux boucler sur les points de Gauss, ou les éléments ?
En effet, on peut :
- Soit calculer les coordonnées réelles de chaque point de Gauss vis à vis de tous les éléments, puis changer de point de Gauss,
- Soit calculer des coordonnées réelles de tout les points de Gauss d'un élément, puis changer d'élément
En réalité, la deuxième méthode est préférable, pour préserver une certaine organisation du fichier de points ainsi obtenu. Si, par la suite, on veut sommer les valeurs de ces n points de Gauss, il suffira, pour l'élément n de lire les points 9(n-1)+1 à 9n (Cas d'une intégration à 3x3 points de Gauss).
Avec la première solution, il aurait été nécessaire de se déplacer constamment dans le fichier, et cela d'une valeur dépendante du maillage : Le point de Gauss i+1 d'un élément est en effet situé N points plus loin que le point de Gauss i de ce même élément. N étant le nombre d'éléments de la structure.
Il apparaît donc bien plus astucieux d'opérer selon la deuxième méthode.
L'algorithme de calcul des coordonnées des points de Gauss sera donc le suivant :
Figure A.1:
Organigramme de calcul des points de Gauss
|
|



suivant: Calcul de la base
monter: Contrôle de la qualité
précédent: Bibliographie
Table des matières
greg
2001-08-07