Index of /besson/slides/2017_09__Presentation_article_CrownCom_Conference
---
author:
__Lilian Besson__ and Rémi Bonnefoi
and Christophe Moy and Émilie Kaufmann and Jacques Palicot
title: MAB Learning in IoT Networks. Learning helps even in non-stationary settings!
institute:
PhD Student in France
Team SCEE, IETR, CentraleSupélec, Rennes
\& Team SequeL, CRIStAL, Inria, Lille
conference: CROWNCOM 2017
date: 20-21 sept 2017
lang: english
---
> Hey, we got the **Best Paper Award** during the [CrownCom 2017](http://crowncom.org/2017/) conference for [this article](https://hal.inria.fr/hal-01575419).
> This document is a raw version of the slides [I (Lilian Besson)](http://perso.crans.org/besson/) used to present our article.
> Please see the [PDF (4:3)](http://perso.crans.org/besson/publis/slides/2017_09__Presentation_article_CrownCom_Conference/slides.pdf) or [PDF (16:9)](http://perso.crans.org/besson/publis/slides/2017_09__Presentation_article_CrownCom_Conference/slides_169.pdf) for a nice version of these slides.
# We want
A *lot* of IoT devices want to access to a gateway of base station.
- Insert them in a **crowded wireless network**.
- With a protocol **slotted in time and frequency**.
- Each device has a **low duty cycle**
(a few messages per day).
## Goal
- Maintain a **good Quality of Service**.
- **Without** centralized supervision!
## How?
- Use **learning algorithms**:
devices will learn on which frequency they should talk!
----
# Outline
1. Introduction and motivation
2. Model and hypotheses
3. Baseline algorithms :
to compare against naive and efficient centralized approaches
4. Two Multi-Armed Bandit algorithms :
UCB, Thompson sampling
5. Experimental results
6. Perspectives and future works
7. Conclusion
----
# Model
- Discrete time $t\geq1$ and $N_c$ radio channels (*e.g.*, 10)
(*known*)
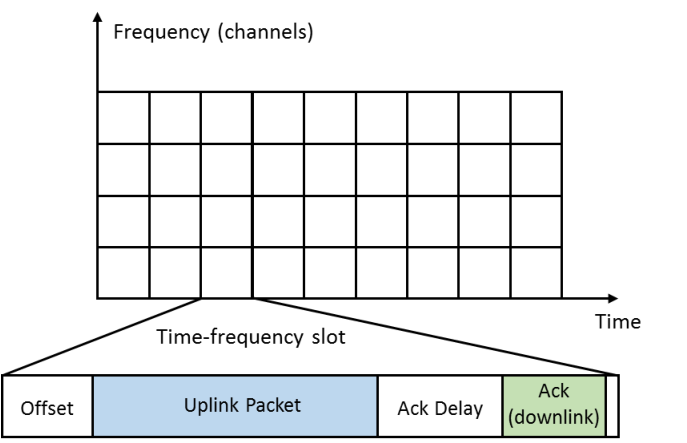
- $D$ **dynamic** devices try to access the network *independently*
- $S=S_1+\dots+S_{N_c}$ **static** devices occupy the network :
$S_1,\dots,S_{N_c}$ in each channel
(*unknown*).
----
# Hypotheses
## Emission model
- Each device has the same *low* emission probability:
each step, each device sends a packet with probability $p$.
(this gives a duty cycle proportional to $1/p$)
## Background traffic
- Each static device uses only one channel.
- Their repartition is fixed in time.
> $\implies$ Background traffic, bothering the dynamic devices!
## Dynamic radio reconfiguration
- Each **dynamic device decides the channel it uses to send every packet**.
- It has memory and computational capacity to implement basic decision algorithm.
## Problem
- *Goal* : *maximize packet loss ratio ($=$ number of received `Ack`)
in a *finite-space discrete-time Decision Making Problem*.
- *Solution ?* **Multi-Armed Bandit algorithms**,
**decentralized** and used **independently** by each device.
----
# A naive strategy : uniformly random access
- **Uniformly random access**:
dynamic devices choose uniformly their channel in the pull of $N_c$ channels.
- Natural strategy, dead simple to implement.
- Simple analysis, in term of **successful transmission probability** (for every message from dynamic devices) :
$$\mathbb{P}(\text{success}|\text{sent}) = \sum_{i=1}^{N_c} \underbrace{(1 - p / N_c)^{D-1}}_{\text{No other dynamic device}} \times \underbrace{(1-p)^{S_i}}_{\text{No static device}} \times\; \frac{1}{N_c}.$$
- Works fine only if all channels are similarly occupied,\newline
but **it cannot learn** to exploit the best (more free) channels.
----
# Optimal centralized strategy
- If an oracle can decide to affect $D_i$ dynamic devices to channel $i$,
the **successful transmission probability** is:
$$\mathbb{P}(\text{success}|\text{sent}) = \sum_{i=1}^{N_c} \underbrace{(1 - p)^{D_i - 1}}_{\;\;D_i - 1 \;\text{others}\;\;} \times \underbrace{(1 - p)^{S_i}}_{\;\;\text{No static device}\;\;} \times \underbrace{ D_i / D }_{\;\;\text{Sent in channel}\; i}.$$
- The oracle has to solve this **optimization problem**:
$$\underset{D_1,\dots,D_{N_c}}{\arg\max}\;\;\; & \sum_{i=1}^{N_c} D_i (1 - p)^{S_i + D_i -1}\\
\text{such that}\;\;\; & \sum_{i=1}^{N_c} D_i = D \; \text{and} \; D_i \geq 0, \; \; \forall 1 \leq i \leq N_c .$$
- We solved this quasi-convex optimization problem with *Lagrange multipliers*, only numerically.
- $\implies$ Very good performance, maximizing the transmission rate of all the $D$ dynamic devices
## But unrealistic
But **not achievable in practice**: no centralized oracle!
## Let see *realistic decentralized approaches*
- $\hookrightarrow$ Machine Learning ?
- $\hookrightarrow$ Reinforcement Learning ?
- $\hookrightarrow$ *Multi-Armed Bandit* !
----
# Multi-Armed Bandit formulation
A dynamic device tries to collect *rewards* when transmitting :
- at each time step $\tau$ when its Bernoulli emission process tells it to communicate,
- chooses a channel $A(\tau) \in \{1,\dots,N_c\}$,
- if `Ack` (no collision)
$\implies$ reward $r_{A(\tau)} = 1$,
- if collision (no `Ack`)
$\implies$ reward $r_{A(\tau)} = 0$.
## Reinforcement Learning interpretation
Maximize transmission rate $\equiv$ **maximize cumulated rewards**
$$\max_{\text{algorithm}\;A} \;\; \sum_{\tau=1}^{\text{horizon}} r_{A(\tau)}.$$
# Upper Confidence Bound algorithm ($\mathrm{UCB}_1$)
A dynamic device keeps $\tau$ number of sent packets, $T_k(t)$ selections of channel $k$, $X_k(t)$ successful transmission in channel $k$.
1. For the first $N_c$ steps ($\tau=1,\dots,N_c$), try each channel *once*.
2. Then for the next steps $t \geq N_c$ :
- Compute the index $g_k(\tau) := \underbrace{\frac{X_k(\tau)}{N_k(\tau)}}_{\text{Mean}\; \widehat{\mu_k}(\tau)} + \underbrace{\sqrt{\frac{\log(\tau)}{2 N_k(\tau)}}.}_{\text{Upper Confidence Bound}}$
- Choose channel $A(\tau) = \mathop{\arg\max}\limits_{k} \; g_k(\tau)$,
- Update $T_k(\tau+1)$ and $X_k(\tau+1)$.
> *References*: [Lai \& Robbins, 1985], [Auer et al, 2002], [Bubeck \& Cesa-Bianchi, 2012].
----
# Thompson Sampling : Bayesian approach
A dynamic device assumes a stochastic hypothesis on the background traffic, modeled as Bernoulli distributions.
- Rewards $r_k(\tau)$ are assumed to be *i.i.d.* samples from a Bernoulli distribution $\mathrm{Bern}(\mu_k)$.
- A **binomial Bayesian posterior** is kept on the mean availability $\mu_k$ : $\mathrm{Bin}(1 + X_k(\tau), 1 + N_k(\tau) - X_k(\tau))$.
- Starts with a *uniform prior* : $\mathrm{Bin}(1, 1) \sim \mathcal{U}([0,1])$.
1. Each step $\tau \geq 1$, a sample is drawn from each posterior
$i_k(t) \sim \mathrm{Bin}(a_k(\tau), b_k(\tau))$,
2. Choose channel $A(\tau) = \mathop{\arg\max}\limits_k \; i_k(\tau)$,
3. Update the posterior after receiving `Ack` or if collision.
> *References*: [Thompson, 1935], [Kaufmann et al, 2012].
----
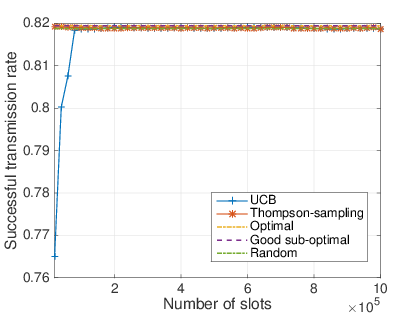
# Experimental setting
## Simulation parameters
- $N_c = 10$ channels,
- $S + D = 10000$ devices in total,
- $p = 10^{-3}$ probability of emission,
- $\text{horizon} = 10^5$ time slots ($\simeq 100$ messages $/$ device),
- The proportion of dynamic devices $D/(S+D)$ varies,
- Various settings for $(S_1,\dots,S_{N_c})$ static devices repartition.
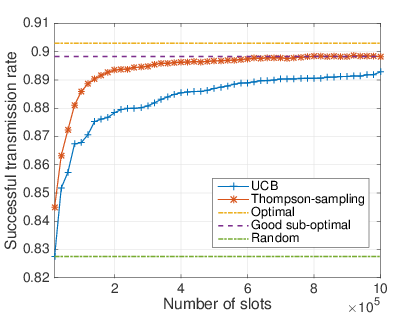
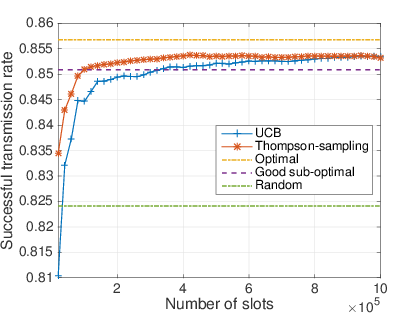
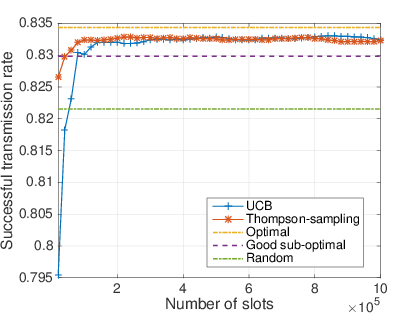
## What do we show
- After a short learning time, MAB algorithm are almost as efficient as the oracle solution.
- Never worse than the naive solution.
- Thompson sampling is even more efficient than UCB.
----
# $10\%$ of dynamic devices
----
# $30\%$ of dynamic devices
----
# $50\%$ of dynamic devices
----
# $100\%$ of dynamic devices (extreme case)
----
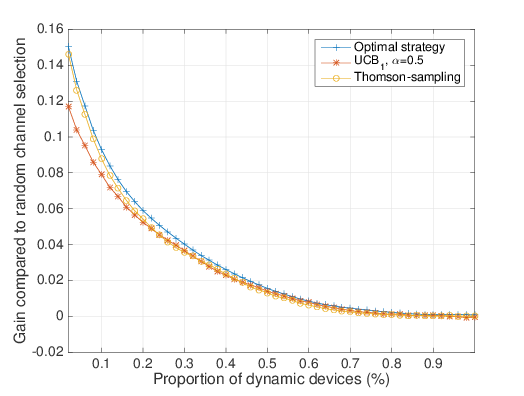
# Dependence on $D/(S+D)$
----
# Perspectives
## Theoretical results
- MAB algorithms have performance guarantees for *stochastic settings*,
- But here the collisions cancel the *i.i.d.* hypothesis,
- Not easy to obtain guarantees in this mixed setting
(*i.i.d.* emission process, game theoretic collisions).
## Real-world experimental validation ?
- Real-world radio experiments will help to validate this.
*In progress*...
----
# Other direction of future work
- *More realistic emission model*:
maybe driven by number of packets in a whole day,
instead of emission probability.
- Validate this on a *larger experimental scale*.
----
## We showed numerically...
- After a learning period, MAB algorithms are almost as efficient as the oracle solution,
- Never worse than the naive solution.
- Thompson sampling is even more efficient than UCB.
- Simple algorithms are up-to $16\%$ more efficient than the naive approach.
## But more work is still needed...
- **Theoretical guarantees** are still missing.
- Maybe study **other emission models**.
- And also implement this on **real-world radio devices**.
> **Thanks!** *Question?*
![[ICO]](/besson/autoindex_strapdown/icons/blank.svg){kind=icon}
![[PARENTDIR]](/besson/autoindex_strapdown/icons/glyphicon-circle-arrow-up.svg){kind=icon}
![[ ]](/besson/_static/icons/pdf.png){kind=icon}
![[IMG]](LogoIETR.png)
![[IMG]](LogoCS.png)
![[IMG]](LogoInria.jpg)
![[ ]](/besson/_static/icons/eps.png){kind=icon}
![[IMG]](perf_learning.png)
![[IMG]](protocol.png)
![[IMG]](30intelligent.png)
![[IMG]](10intelligent.png)
![[IMG]](50intelligent.png)
![[IMG]](100intelligent.png)
![[TXT]](/besson/autoindex_strapdown/icons/glyphicon-file.svg){kind=icon}