The research of the best enrichment function

To solve this problem, I examined the one-dimensional case, for a two phases problem. The objective is to find the enrichment function which gives the smallest amount of error regardless of the position of the front in the element. I assumed that this function was the same in dynamic case and in the steady-state case.

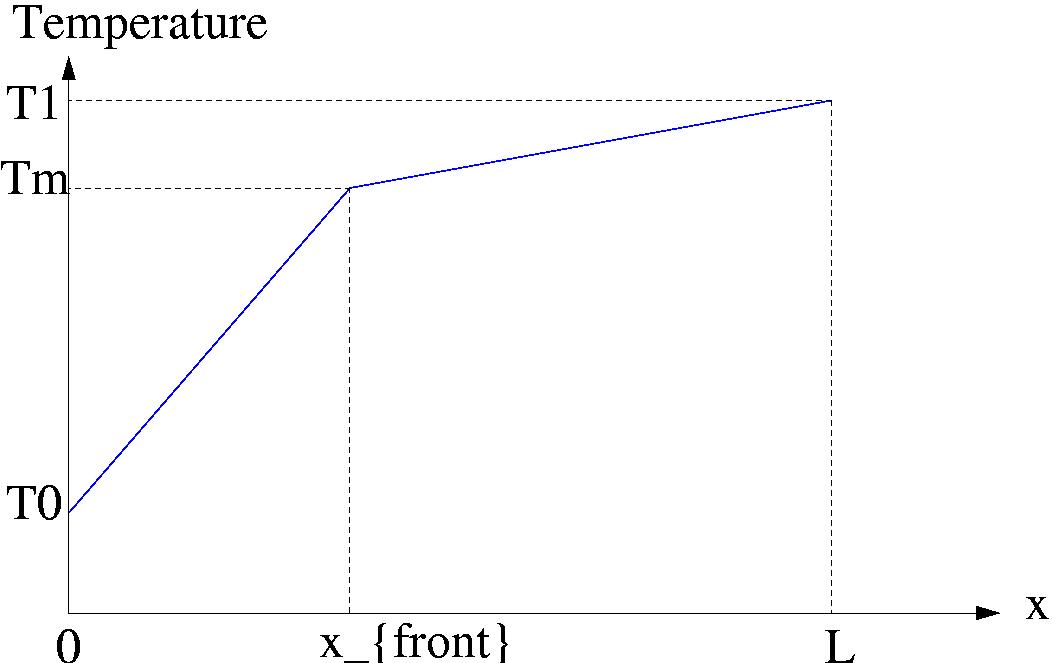
The problem is basicly the following: find a function which gives the less amount of error for solving a field where there is a discontinuity in the spatial derivative (see Fig. 21).

Figure 21: The exact field to solve.

The main idea is that the Gallerkin approximation looks the best like the exact solution .

To best describe the local behavior of the solution, we have assumed that the enrichment was equal to 0 in the elements non cut by the interface.

The general constraint are:

• must be continuous.
• must be discontinuous.

From the second proposition, we can deduce that the function is continuous, which means:

This leads to two possibles cases:

• : in this case, g is continuous.
• : in this case, g can be discontinuous.