|
The stationary mesh:
The stationary mesh method consists of a classical finite element approximation with a fixed
mesh over time. For the case here of one-dimension, the mesh is composed by linearly equally
spaced points. The grid does not depend on the position of the front during time.
Each element is a segment, its length is
where
represents the length of the domain and
the number of elements.
This method does not need to rebuild the mass and stiffness matrices every
time step.
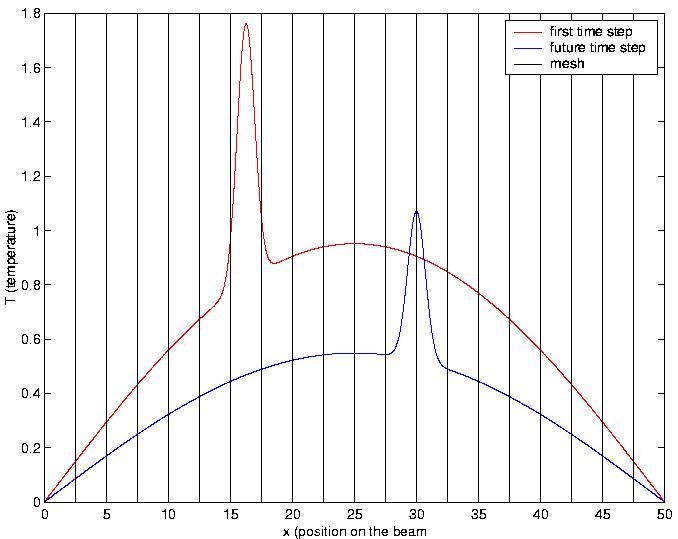
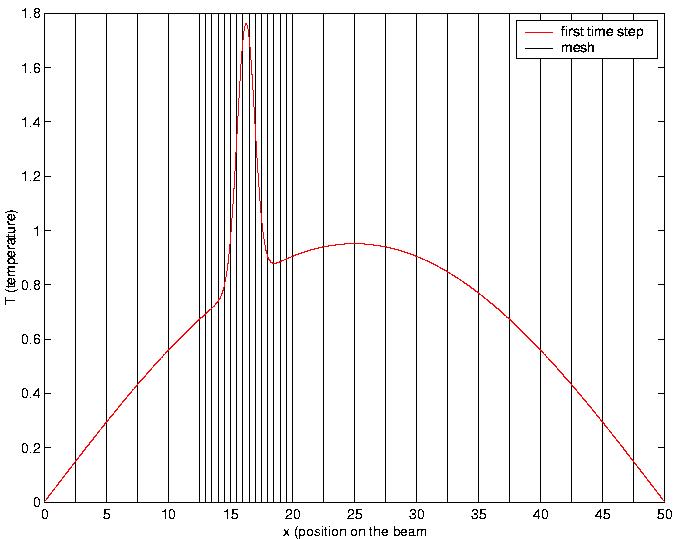
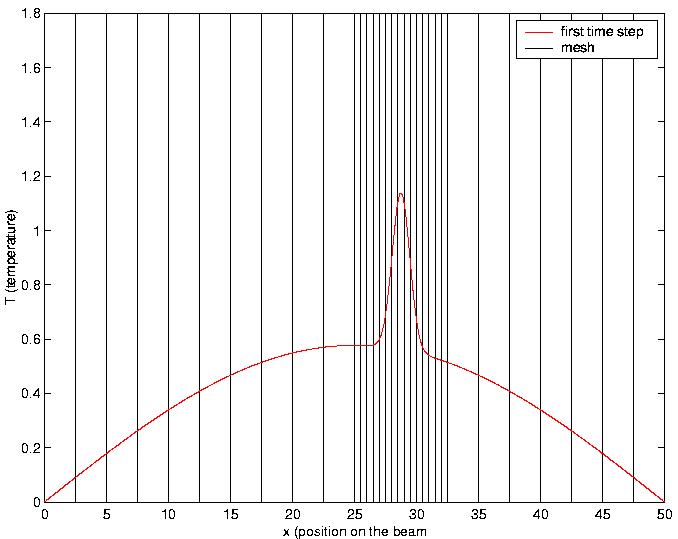
The moving mesh:
The moving mesh method consists of remeshing the domain at each time step depending upon the position of the front during time. The mesh is composed by a coarse background mesh and a fine mesh in the vicinity of the front. In our case, the coarse mesh is composed by 20 elements, the region where the mesh is thiner is .
|
|
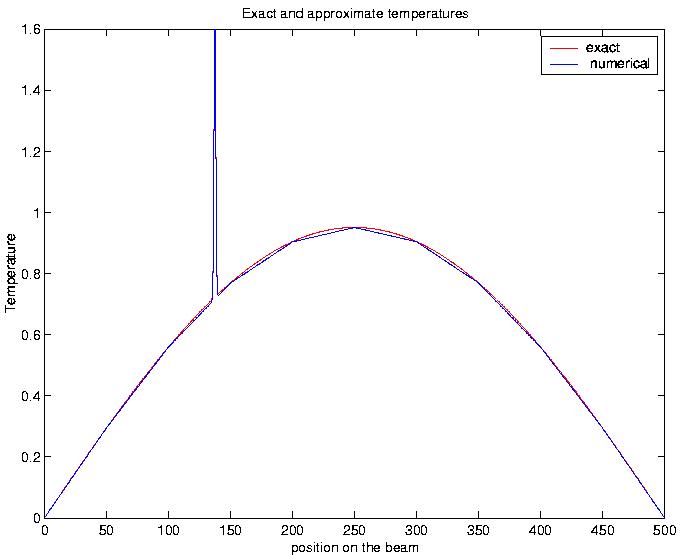
Results: the comparison between the methods:
The results have been computed for 36 time iterations. We have used the and norm to measure the error.
and represents the sum of the and error over the time steps.
| Number of elements | X-FEM | FEM, stationnary mesh | ||
| 20 | 0.65 | 1.73 | 18.34 | 27.79 |
| 100 | 17.82 | 25.43 | ||
| 200 | 6.69 | 19.33 | ||
| 400 | 2.64 | 18.34 | ||
|
|
|