Index of /besson/slides/2018_04__Presentation_at_ALT_2018_conference
---
author:
__Lilian Besson__ *Advised by Christophe Moy Émilie Kaufmann
title: Multi-Player Bandits Models Revisited
subtitle: Decentralized Multi-Player Multi-Arm Bandits
institute:
PhD Student,
Team SCEE, IETR, CentraleSupélec, Rennes
& Team SequeL, CRIStAL, Inria, Lille
date: ALT 2018 Conference - 08 April 2018
lang: english
---
# Motivation
We control some communicating devices,
they want to access to a single base station.
- Insert them in a **crowded wireless network**.
- With a protocol **slotted in both time and frequency**.
## Goal
- Maintain a **good Quality of Service**.
- **With no centralized control** as it costs network overhead.
## How?
- Devices can choose a different radio channel at each time
→ learn the best one with sequential algorithm!
----
# Outline and reference
1. Introduction
2. Our model: 3 different feedback levels
3. Decomposition and lower bound on regret
4. Quick reminder on single-player MAB algorithms
5. Two new multi-player decentralized algorithms
6. Upper bounds on regret for MCTopM
7. Experimental results
8. An heuristic (Selfish), and disappointing results
9. Conclusion
This is based on our latest article:
- "Multi-Player Bandits Models Revisited", Besson & Kaufmann. [arXiv:1711.02317](https://arXiv.org/abs/1711.02317)
----
# Our model
- K radio channels (*e.g.*, 10) (*known*)
- Discrete and synchronized time t >= 1. Every time frame t is:
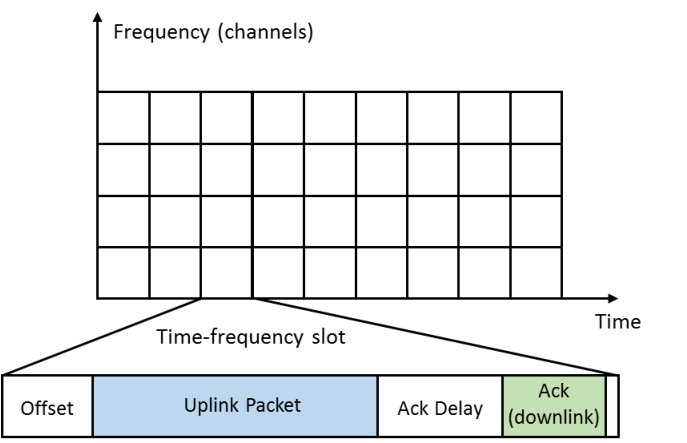
## Dynamic device = dynamic radio reconfiguration
- It decides **each time** the channel it uses to send **each packet**.
- It can implement a simple **decision algorithm**.
----
# Our model
## "Easy" case
- M <= K devices **always communicate** and try to access the network,
*independently* without centralized supervision,
- Background traffic is *i.i.d.*.
## Two variants : with or without *sensing*
1. *With sensing*:
Device first senses for presence of Primary Users (background traffic), then use `Ack` to detect collisions.
Model the "classical" Opportunistic Spectrum Access problem.
Not exactly suited for *Internet of Things*, but can model ZigBee, and can be analyzed mathematically...
2. *Without sensing*: same background traffic, but cannot sense, so only `Ack` is used.
More suited for "IoT" networks like LoRa or SigFox.
(Harder to analyze mathematically.)
----
# Background traffic, and rewards
## *i.i.d.* background traffic
- K channels, modeled as Bernoulli (0/1) distributions of mean µ_k
= background traffic from *Primary Users*, bothering the dynamic devices,
- M devices, each uses channel A^j(t) in {1,...,K} at time t.
## Rewards
r^j(t) := Y_{A^j(t),t} × 1(not C^j(t)) = 1(uplink & Ack).
- with sensing information for all k, Y_{k,t} ~ Bern(µ_k) in {0, 1},
- collision for device j :
C^j(t) = 1(*alone on arm A^j(t)*).
→ joint binary reward **but not** from two Bernoulli!
----
# 3 feedback levels
r^j(t)} := Y_{A^j(t),t} × 1(not C^j(t))
1. "Full feedback": observe both Y_{A^j(t),t} *and* C^j(t) separately,
→ Not realistic enough, we don't focus on it.
2. "Sensing": first observe Y_{A^j(t),t}, *then* C^j(t) only if Y_{A^j(t),t} != 0,
→ Models licensed protocols (ex. ZigBee), our main focus.
3. "No sensing": observe only the joint Y_{A^j(t),t} × 1(not C^j(t)),
→ Unlicensed protocols (ex. LoRaWAN), harder to analyze !
But all consider the same instantaneous reward r^j(t).
----
# Goal
## Problem
- *Goal* : *minimize packet loss ratio* (= maximize nb of received `Ack`)
in a *finite-space discrete-time Decision Making Problem*.
- *Solution ?* **Multi-Armed Bandit algorithms**,
**decentralized** and used **independently** by each dynamic device.
## *Decentralized* reinforcement learning optimization!
- Max transmission rate = **max cumulated rewards**
max_{text{algorithm} A} sum_{t=1}^{T} sum_{j=1}^M r^j_{A(t)}.
- Each player wants to **maximize its cumulated reward**,
- With no central control, and no exchange of information,
- Only possible if : each player converges to one of the M best arms,
orthogonally (without collisions).
----
# Centralized regret
## A measure of success
- Not the network throughput or collision probability,
- We study the **centralized** (expected) **regret**:
R_T(µ, M, rho)
:= E_µ[ sum_{t=1}^T sum_{j=1}^M µ_j^* - r^j(t)]
= (sum_{k=1}^{M}µ_k^*) T - E_µ[sum_{t=1}^T sum_{j=1}^M r^j(t)]
## Two directions of analysis
- Clearly R_T = O(T), but we want a sub-linear regret, as small as possible!
- *How good a decentralized algorithm can be in this setting?*
→ **Lower Bound** on regret, for **any** algorithm !
- *How good is my decentralized algorithm in this setting?*
→ **Upper Bound** on regret, for **one** algorithm !
----
# Lower bound
1. Decomposition of regret in 3 terms,
2. Asymptotic lower bound of one term,
3. And for regret,
4. Sketch of proof,
5. Illustration.
----
# Decomposition on regret
## Decomposition
For any algorithm, decentralized or not, we have
R_T(µ, M, rho) = sum_{k in M-worst} (µ_M^* - µ_k) E_µ[T_k(T)] + sum_{k in M-best} (µ_k - µ_M^*) (T - E_µ[T_k(T)]) + sum_{k=1}^{K} µ_k E_µ[C_k(T)].
## Small regret can be attained if...
1. Devices can quickly identify the bad arms M-worst, and not play them too much
(*number of sub-optimal selections*),
2. Devices can quickly identify the best arms, and most surely play them
(*number of optimal non-selections*),
3. Devices can use orthogonal channels
(*number of collisions*).
# Asymptotic Lower Bound on regret
## 3 terms to lower bound...
- The first term for sub-optimal arms selections
is lower bounded asymptotically,
for all player j, bad arm k, lim inf (T → oo) E_µ[T_k^j(T)] / \log T >= 1 / kl(µ_k, µ_M^*),
using technical information theory tools
(Kullback-Leibler divergence, entropy),
- And we lower bound the rest (including collisions) by... 0
T - E_µ[T_k(T)] >= 0 and E_µ[C_k(T)] >= 0,
😭 we should be able to do better!
# Asymptotic Lower Bound on regret
## Theorem 1 [Besson & Kaufmann, 2017]
- For any uniformly efficient decentralized policy, and any non-degenerated problem µ,
lim inf (T → oo) R_T(µ, M, rho) / log(T) >= M × ( sum_{k in M-worst} (µ_M^* - µ_k) / kl(µ_k, µ_M^*) ) .
Where kl(x,y) := x log(x / y) + (1 - x) log(1-x / 1-y) is the *binary* Kullback-Leibler divergence.
## Remarks
- The centralized *multiple-play* lower bound is the same without the M multiplicative factor...
Ref: [Anantharam et al, 1987]
→ "price of non-coordination" = M = nb of player?
- Improved state-of-the-art lower bound, but still not perfect: collisions should also be controlled!
----
# Illustration of the Lower Bound on regret
----
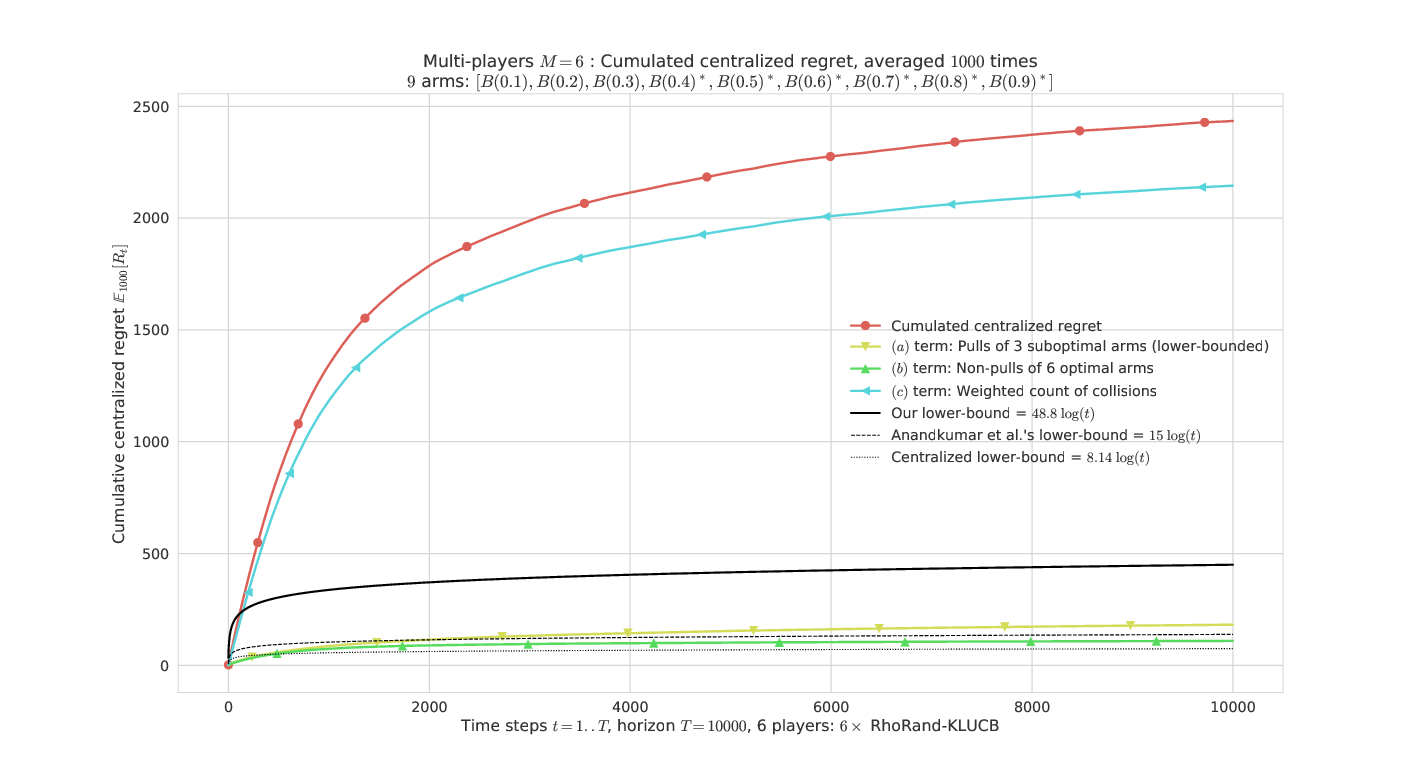
# Sketch of the proof
- Like for single-player bandit, focus on E_µ[T_k^j(T)] expected number of selections of any sub-optimal arm k.
- Same information-theoretic tools, using a "change of law" lemma. Ref: [Garivier et al, 2016]
- It improved the state-of-the-art because of our decomposition, not because of new tools.
> → See our paper for details!
----
# Single-player MAB algorithms
1. Index-based MAB deterministic policies,
2. Upper Confidence Bound algorithm : UCB,
3. Kullback-Leibler UCB algorithm : klUCB.
----
# Upper Confidence Bound algorithm UCB1
The device keep t number of sent packets, T_k(t) selections of channel k, X_k(t) successful transmissions in channel k.
1. For the first K steps (t=1,...,K), try each channel *once*.
2. Then for the next steps t > K :
- Compute the index g_k(t) := X_k(t) / T_k(t) + sqrt{log(t) / 2 T_k(t)}
- Choose channel A(t) = arg max_k g_k(t),
- Update T_k(t+1) and X_k(t+1).
References: [Lai & Robbins, 1985], [Auer et al, 2002], [Bubeck & Cesa-Bianchi, 2012]
----
# Kullback-Leibler UCB algorithm klUCB
The device keep t number of sent packets, T_k(t) selections of channel k, X_k(t) successful transmissions in channel k.
1. For the first K steps (t=1,...,K), try each channel *once*.
2. Then for the next steps t > K :
- Compute the index g_k(t) := sup_{q in [a, b]} { q : kl(X_k(t) / T_k(t), q) <= log(t) / T_k(t) }
- Choose channel A(t) = arg max_k g_k(t),
- Update T_k(t+1) and X_k(t+1).
*Why bother?* klUCB is proved to be more efficient than UCB,
and asymptotically optimal for single-player stochastic bandit.
References: [Garivier & Cappé, 2011], [Cappé & Garivier & Maillard & Munos & Stoltz, 2013]
----
# Multi-player decentralized algorithms
1. Common building blocks of previous algorithms,
2. First proposal: RandTopM,
3. Second proposal: MCTopM,
4. Algorithm and illustration.
----
# Algorithms for this easier model
## Building blocks : separate the two aspects
1. **MAB policy** to learn the best arms (use sensing Y_{A^j(t),t}),
2. **Orthogonalization scheme** to avoid collisions (use C^j(t)).
## Many different proposals for *decentralized* learning policies
- Recent: MEGA and MusicalChair, [Avner & Mannor, 2015], [Shamir et al, 2016]
- State-of-the-art: rhoRand policy and variants. [Anandkumar et al, 2011]
## **Our proposals**: [Besson & Kaufmann, 2017]
- *With sensing*: RandTopM and MCTopM are sort of mixes between rhoRand and MusicalChair, using UCB indexes or more efficient index policies (klUCB),
- *Without sensing*: Selfish use a UCB index directly on the reward r^j(t).
----
# A first decentralized algorithm
----
# The RandTopM algorithm
----
# The MCTopM algorithm
----
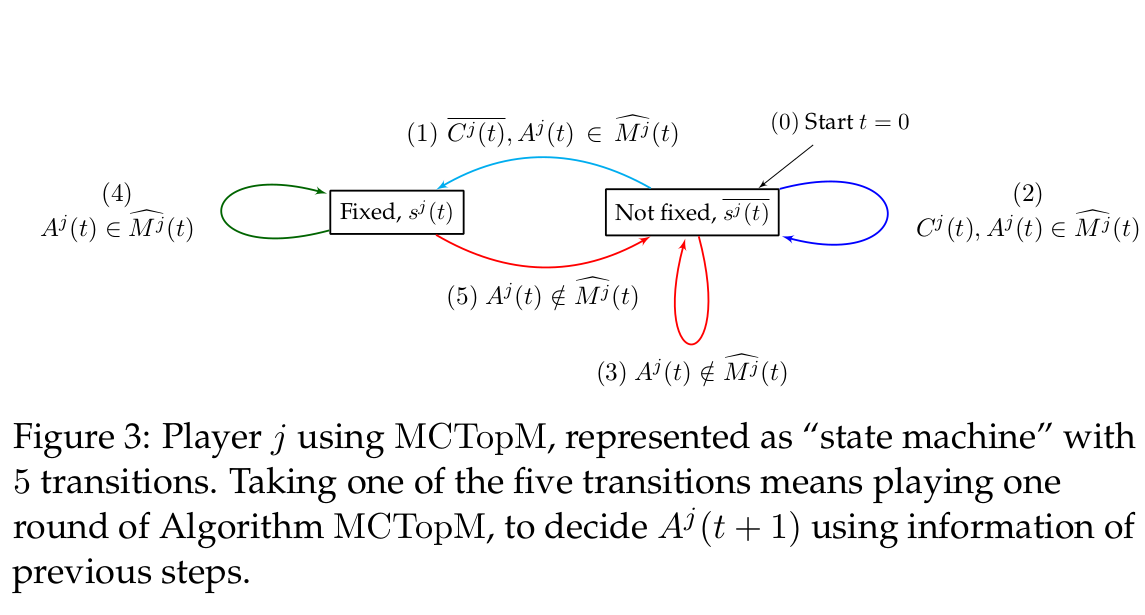
# The MCTopM algorithm
----
# Regret upper bound
1. Theorem,
2. Remarks,
3. Idea of the proof.
----
# Regret upper bound for MCTopM
## Theorem 2 [Besson & Kaufmann, 2017]
- If all M players use MCTopM with klUCB,
then for any non-degenerated problem µ,
there exists a problem dependent constant G_{M,µ}
, such that the regret satisfies:
R_T(µ, M, rho) \leq G_{M,µ} log(T) + \smallO{\log T}.
## How?
- Decomposition of regret controlled with two terms,
- Control both terms, both are logarithmic:
+ Suboptimal selections with the "classical analysis" on klUCB indexes
+ Collisions are harder to control...
----
# Regret upper bound for MCTopM
## Remarks
- Hard to prove, we had to carefully design the MCTopM algorithm to conclude the proof,
- The constant G_{M,µ} scales as M^3, way better than rhoRand's constant scaling as M{2M-1 \choose M},
- We also *minimize the number of channel switching*: interesting as changing arm costs energy in radio systems,
- For the suboptimal selections, we *match our lower bound* !
- Not yet possible to know what is the best possible control of collisions...
----
# Sketch of the proof
1. Bound the expected number of collisions by M times the number of collisions for non-sitted players,
2. Bound the expected number of transitions of type (3) and (5), by \bigO{\log T} using the klUCB indexes and the forced choice of the algorithm:
g_k^j(t-1) \leq g^j_{k'}(t-1), and} g_k^j(t) > g^j_{k'}(t)
when switching from k' to k,
3. Bound the expected length of a sequence in the non-sitted state by a constant,
4. So most of the times (O(T - log T)), players are sitted, and no collision happens when they are all sitted!
> → See our paper for details!
----
# Experimental results
> Experiments on Bernoulli problems µ in [0,1]^K.
1. Illustration of regret for a single problem and M = K,
2. Regret for uniformly sampled problems and M < K,
3. Logarithmic number of collisions,
4. Logarithmic number of arm switches,
5. Fairness?
----
# Constant regret if M = K
Regret, M=9 players, K=9 arms, horizon T=10000, 200 repetitions. Only RandTopM and MCTopM achieve constant regret in this saturated case (proved).
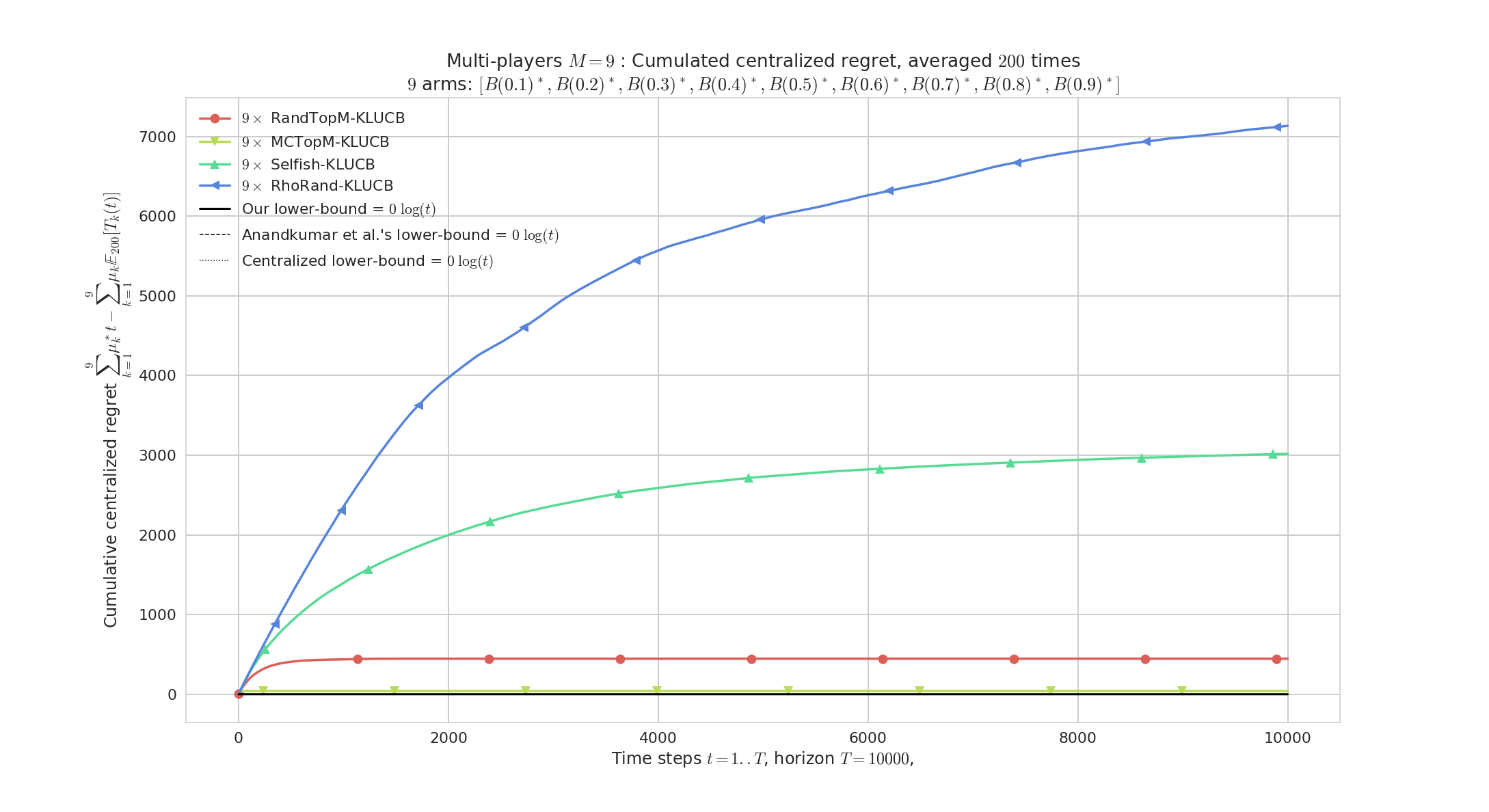
# Illustration of regret of different algorithms
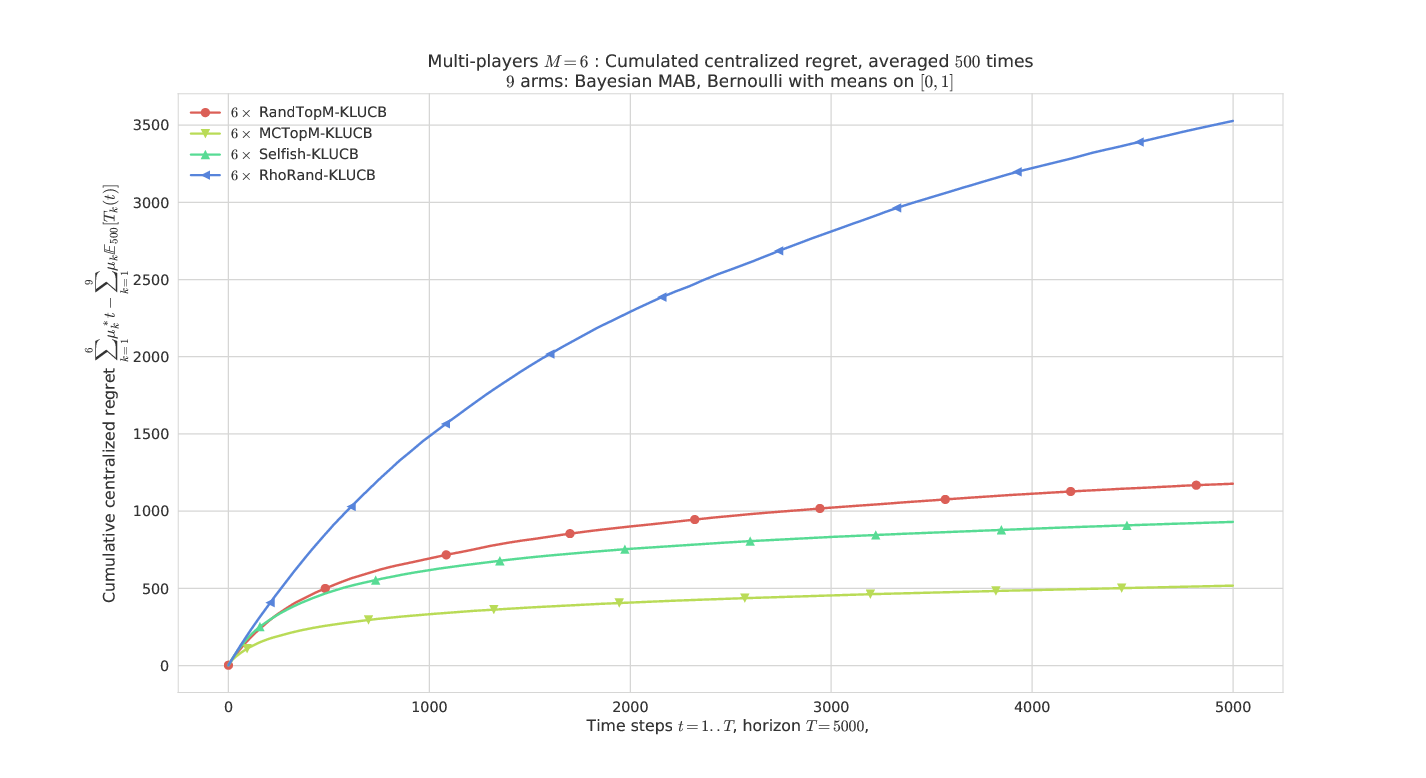
Regret, M=6 players, K=9 arms, horizon T=5000, against 500 problems µ uniformly sampled in [0,1]^K. Conclusion : rhoRand < RandTopM < Selfish < MCTopM in most cases.
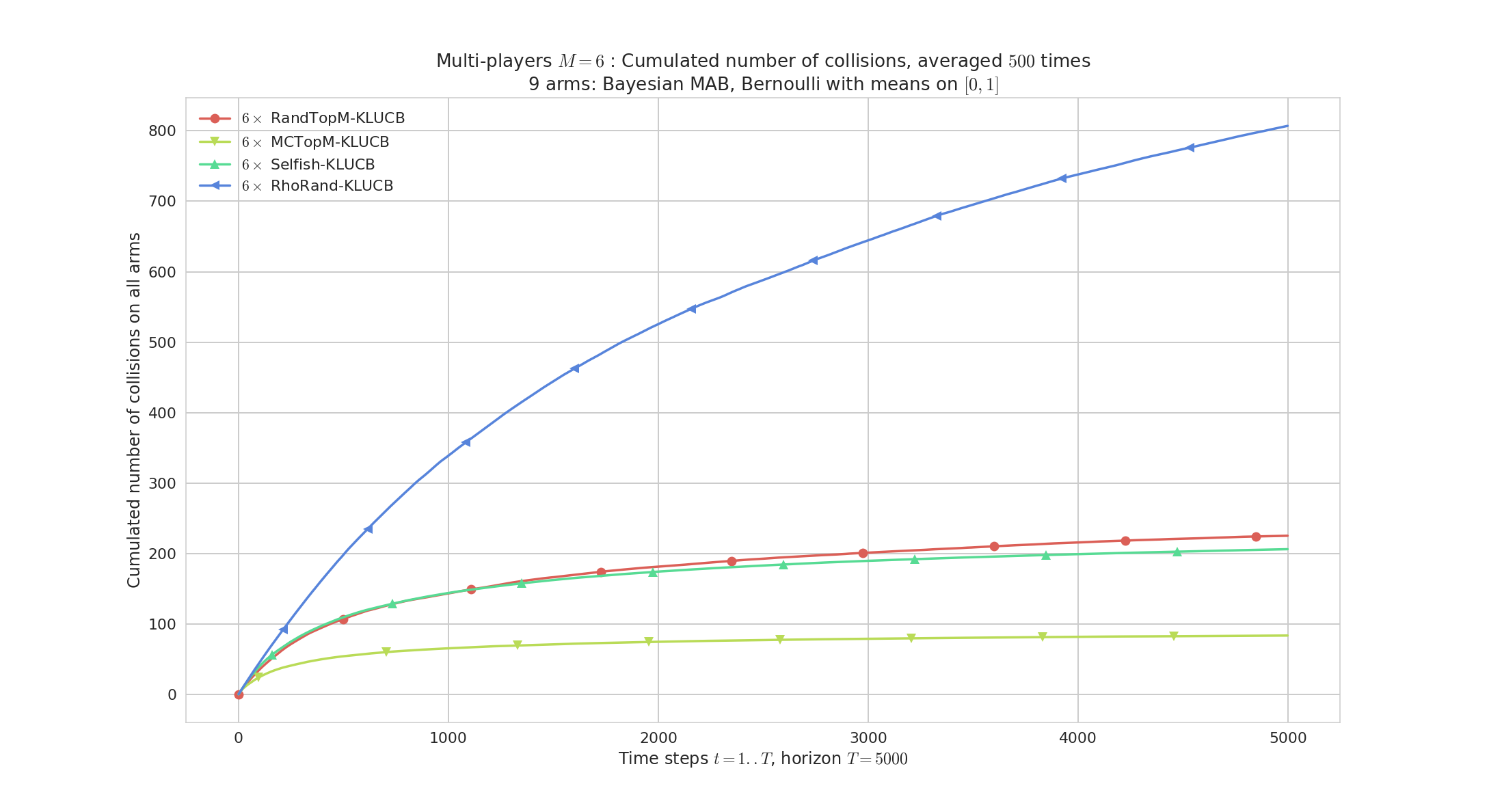
# Logarithmic number of collisions
Cumulated number of collisions. Also rhoRand < RandTopM < Selfish < MCTopM in most cases.
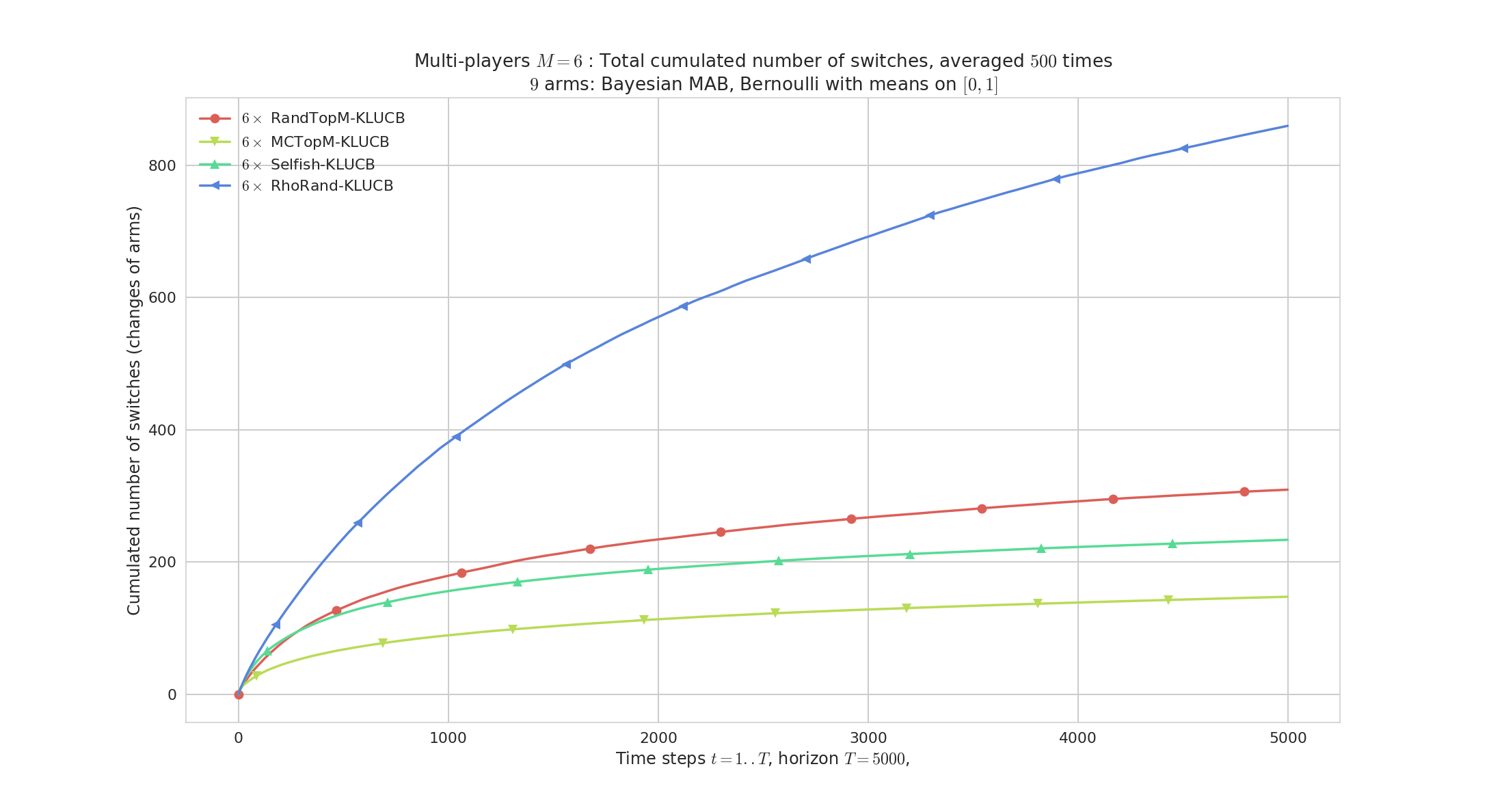
# Logarithmic number of arm switches
Cumulated number of arm switches. Again rhoRand < RandTopM < Selfish < MCTopM, but no guarantee for rhoRand.
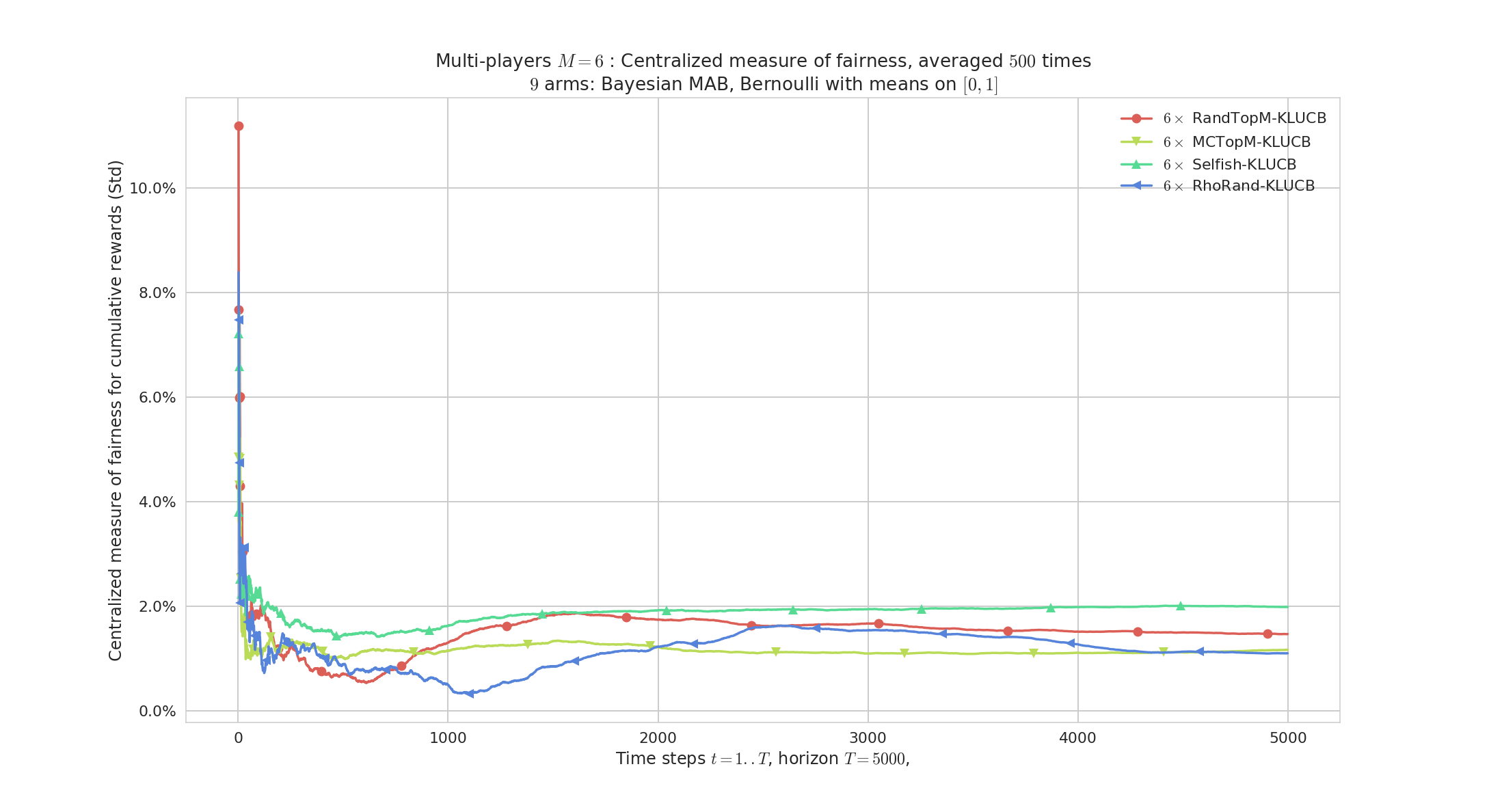
# Fairness
Measure of fairness among player. All 4 algorithms seem fair in average, but none is fair on a single run It's quite hard to achieve both efficiency and single-run fairness!
----
# An heuristic, Selfish
For the harder feedback model, without sensing.
1. Just an heuristic,
2. Problems with Selfish,
5. Illustration of failure cases.
----
# The Selfish heuristic
The Selfish decentralized approach = device don't use sensing, just learn on the reward (acknowledgement or not, r^j(t)).
Reference: [Bonnefoi & Besson et al, 2017]
## Works fine...
- More suited to model IoT networks,
- Use less information, and don't know the value of M: we expect Selfish to not have stronger guarantees.
- It works fine in practice!
## *But why would it work?*
- Sensing was *i.i.d.* so using UCB to learn the µ_k makes sense,
- But collisions are not *i.i.d.*,
- Adversarial algorithms are more appropriate here,
- But empirically, Selfish with UCB or klUCB works much better than, *e.g.*, Exp3...
## Works fine...
- Except... when it fails drastically! 😭
- In small problems with M and K = 2 or 3, we found small probability of failures (*i.e.*, linear regret), and this prevents from having a generic upper bound on regret for Selfish.
----
# Illustration of failing cases for Selfish
![Regret for M=2, K=3, T=5000, 1000 repetitions and µ = [0.1, 0.5, 0.9]. Axis x is for regret (different scale for each), and Selfish have a small probability of failure (17/1000 cases of R_T \gg \log T). The regret for the three other algorithms is very small for this "easy" problem.](figures/MP__K3_M2_T5000_N1000__4_algos/all_HistogramsRegret____env1-1_5016720151160452442.png)
----
# Sum-up
## *Wait, what was the problem ?*
- MAB algorithms have guarantees for *i.i.d. settings*,
- But here the collisions cancel the *i.i.d.* hypothesis...
- Not easy to obtain guarantees in this mixed setting
(*i.i.d.* emissions process, "game theoretic" collisions).
## Theoretical results
- With sensing ("OSA"), we obtained strong results: a lower bound, and an order-optimal algorithm,
- But without sensing ("IoT"), it is harder... our heuristic Selfish usually works but can fail!
----
# Other directions of future work
## Conclude the Multi-Player OSA analysis
- Remove hypothesis that objects know M,
- Allow arrival/departure of objects,
- Non-stationarity of background traffic etc
- *More realistic emission model*:
maybe driven by number of packets in a whole day,
instead of emission probability.
## Extend to more objects M > K
- Extend the theoretical analysis to the large-scale IoT model,
first with sensing (*e.g.*, models ZigBee networks),
then without sensing (*e.g.*, LoRaWAN networks).
----
# Conclusion
- In a wireless network with an *i.i.d.* background traffic in K channels,
- M devices can use both sensing and acknowledgement feedback, to learn the most free channels and to find orthogonal configurations.
## We showed 😀
- Decentralized bandit algorithms can solve this problem,
- We have a lower bound for any decentralized algorithm,
- And we proposed an order-optimal algorithm, based on klUCB and an improved Musical Chair scheme, MCTopM
## But more work is still needed... 😕
- **Theoretical guarantees** are still missing for the "IoT" model (without sensing), and can be improved (slightly) for the "OSA" model (with sensing).
- Maybe study **other emission models**...
- Implement and test this on **real-world radio devices**
→ demo (in progress) for the ICT 2018 conference!
## **Thanks!** 😀
*Any question or idea ?*
![[ICO]](/besson/autoindex_strapdown/icons/blank.svg){kind=icon}
![[PARENTDIR]](/besson/autoindex_strapdown/icons/glyphicon-circle-arrow-up.svg){kind=icon}
![[DIR]](/besson/autoindex_strapdown/icons/glyphicon-folder-open.svg){kind=icon}
![[TXT]](/besson/autoindex_strapdown/icons/glyphicon-file.svg){kind=icon}
![[ ]](/besson/_static/icons/pdf.png){kind=icon}