DS 2 : X PSI-PT 2015

2ème DS, algorithmique sur des tableaux 1D et 2D, et simulations probabilistes.

Correction du DS de vendredi 11 décembre 2015.

Voici ci-dessous la documentation de la correction complète du sujet d’écrit d’informatique (Polytechnique et ENS, 2015), pour PSI et PT.

Ce sujet d’écrit a été posé en devoir écrit surveillé (DS) pour le cours d’informatique pour tous en prépa MP au Lycée Lakanal.

Veuillez consulter le code source pour tous les détails svp. Ci dessous se trouve simplement la documentation de ce programme.

Note

Cette correction contient beaucoup de documentation, des exemples et des détails. Pour une correction beaucoup plus concise, voir cette page.

Avertissement

Les fonctions sont ici listées par ordre alphabétique, et pas dans l’ordre du fichier source. D’habitude, j’arrive à corriger ça, mais là non. Désolé. Je trouverai comment régler ce problème !

X_PSI_PT__2015.creerTableau(n)[source]

(Préliminaires) On implémente cette fonction avec un tableau Python (de type list).

  • Créé un tableau vide de taille n et le renvoie.
  • Elle n’était pas demandée, mais supposée donnée.
  • Les valeurs initiales du tableau sont arbitraires (None en pratique).
  • Exemple :
>>> n = 5; t = creerTableau(n)
>>> for i in range(n):
...     t[i] = i + 2
>>> affiche(t)
[2, 3, 4, 5, 6]
X_PSI_PT__2015.creerTableau2D(p, q)[source]

(Préliminaires) Exemple de création d’un tableau bi-dimensionnel, de taille \(p \times q\), ie. un tableau a de p tableaux de taille q.

  • Elle n’était pas demandée, mais est donnée ici à titre d’illustration,
  • Exemple :
>>> p = 2; q = 2;
>>> a = creerTableau2D(p, q)
>>> for i in range(p):
...     for j in range(q):
...         a[i][j] = i+j
>>> affiche(a)
[[0, 1], [1, 2]]
X_PSI_PT__2015.affiche(*args)[source]

(Préliminaires) Affiche les arguments un à un, séparés par des espaces.

  • Elle n’était pas demandée, mais supposée donnée,
  • Exemple :
>>> x = 1; y = x+1
>>> affiche("x = ",x," et y = ",y)
x = 1 et y = 2
X_PSI_PT__2015.creerListeVide(n)[source]

(Question 1) Crée, initialise et renvoie un tableau de longueur n + 1 correspondant à la liste vide ayant une capacité de n éléments.

  • Chaque case du tableau est initialisé à None pour garder trace qu’elle est vide,
  • Exemple :
>>> n = 5; liste = creerListeVide(n)
>>> affiche(liste)
[0, None, None, None, None, None]
X_PSI_PT__2015.estDansListe(liste, x)[source]

(Question 2) Teste si l’élement x apparaît dans la représentée par le tableau liste (répond True ou False).

  • Complexité en temps : \(O(n)\) (dans le pire des cas, car on doit alors parcourir tout le tableau),
  • Complexité en mémoire : \(O(1)\) (toujours),
  • Exemple :
>>> # Exemple d'une liste non ordonnée contenant 1,2,3,4,5
>>> liste = [5, 5, 4, 2, 1, 3]
>>> affiche(estDansListe(liste, 0))
False
>>> affiche(estDansListe(liste, 5))
True
>>> affiche(estDansListe(liste, 194652))
False
X_PSI_PT__2015.ajouteDansListe(liste, x)[source]

(Question 3) Modifie de façon appropriée le tableau liste pour y ajouter x, si l’entier x n’appartient pas déjà à la liste, et ne fait rien sinon.

  • Cette procédure ne fait rien du tout si la liste est pleine initialement (Le sujet ne demandait pas de traiter ce cas),
  • Complexité en temps : \(O(n)\) (dans le pire des cas, car on doit alors parcourir tout le tableau),
  • Complexité en mémoire : \(O(1)\) (toujours),
  • Exemple :
>>> n = 5; liste = creerListeVide(n)
>>> for i in range(1, n+1):
...     ajouteDansListe(liste, 4**i)
>>> affiche(liste)
[5, 4, 16, 64, 256, 1024]
>>> # Très similaire à un ensemble défini par compréhension :
>>> ensemble = { 4**i for i in range(1, n+1)}
>>> affiche(ensemble)  # L'ordre est arbitraire ! set([16, 64, 4, 256, 1024])
{16, 64, 256, 1024, 4}
  • On peut vérifier qu’ajouter un élément quand la liste est déjà pleine ne marche pas (la liste n’est pas modifiée) :
>>> ajouteDansListe(liste, 2015)
Impossible d'ajouter l'élément x = 2015 à la liste [5, 4, 16, 64, 256, 1024] qui est déjà pleine (n = 5).
  • Note : ce message d’erreur n’était pas demandée.
X_PSI_PT__2015.creerPlanSansRoute(n)[source]

(Question 5) Crée, remplit et renvoie le tableau de tableaux correspondant au plan à n villes n’ayant aucune route.

  • Complexité en temps : \(O(n)\) (toujours),
  • Complexité en mémoire : \(O(n)\) (toujours),
  • Exemple :
>>> n = 4; plan = creerPlanSansRoute(n)
>>> affiche(plan)
[[4, 0], [0, None, None, None, None, None], [0, None, None, None, None, None], [0, None, None, None, None, None], [0, None, None, None, None, None]]
  • Note : les None affichées plus haut correspondent aux * dans le sujet.
X_PSI_PT__2015.estVoisine(plan, x, y)[source]

(Question 6) Renvoie True si les villes x et y sont voisines dans le plan codé par le tableau de tableaux plan, et renvoie False sinon.

  • On utilise une structure qui peut représenter des graphes dirigés (ie. non symétrique, on peut avoir \(x \to y\) sans avoir \(y \to x\)), mais tout le reste du sujet n’utilisera que des graphes non dirigés (tous les chemins sont symétriques, donc \(x \sim y \Leftrightarrow x \to y \;\;\text{et}\;\; y \to x\)),
  • Complexité en temps : \(O(n)\) (dans le pire des cas, car on doit alors parcourir toutes les voisines de x et de y),
  • Complexité en mémoire : \(O(1)\) (toujours),
  • Exemple :
>>> plan = [[5, 4], [1, 2, None, None, None], [3, 1, 3, 4, None], [1, 2, None, None, None], [2, 2, 5, None, None], [1, 4, None, None, None]]  # plan2, cf ci-dessus
>>> x = 1; y = 2
>>> affiche(estVoisine(plan, x, y))
True
>>> x = 1; y = 5
>>> affiche(estVoisine(plan, x, y))
False
X_PSI_PT__2015.ajouteRoute(plan, x, y)[source]

(Question 7) Modifie le tableau de tableaux plan pour ajouter une route entre les villes x et y si elle n’était pas déjà présente et ne fait rien sinon.

  • Le sujet disait “On prendra garde à bien mettre à jour toutes les cases concernées dans le tableau de tableaux ``plan``”, ce qui montre bien qu’ils veulent garder le graphe symétrique (cf. explication de la fonction précédente).
  • Le sujet demandait “Y a-t-il un risque de dépassement de la capacité des listes ?”, et non car on les a initialisé avec une capacité de n+1 (cf. creerPlanSansRoute()),
  • Complexité en temps : \(O(n)\) (dans le pire des cas, car on doit alors parcourir toutes les voisines de x et de y),
  • Complexité en mémoire : \(O(1)\) (toujours),
  • Exemple :
>>> plan = [[5, 4], [1, 2, None, None, None], [3, 1, 3, 4, None], [1, 2, None, None, None], [2, 2, 5, None, None], [1, 4, None, None, None]]  # plan2, cf ci-dessus
>>> affiche("Ce plan a m = ", plan[0][1], " route(s).")
Ce plan a m = 4 route(s).
>>> x = 1; y = 5
>>> affiche(estVoisine(plan, x, y))
False
>>> ajouteRoute(plan, x, y)
>>> affiche("Ce plan a m = ", plan[0][1], " route(s).")
Ce plan a m = 5 route(s).
>>> affiche(estVoisine(plan, x, y))
True
X_PSI_PT__2015.afficheToutesLesRoutes(plan)[source]

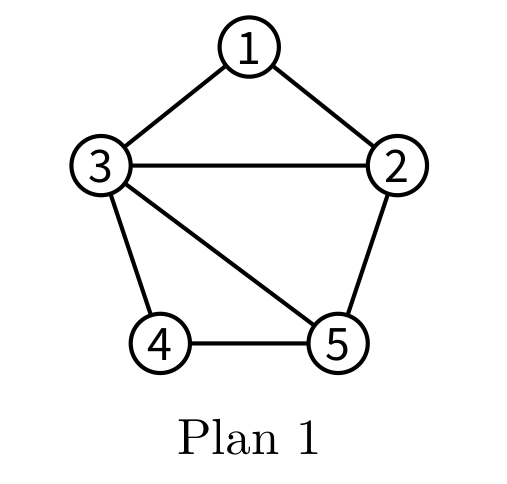
(Question 8) Affiche à l’écran la liste des routes du plan codé par le tableau de tableaux plan, où chaque route apparaît exactement une seule fois.

  • Par exemple, pour le graphe codé par le tableau de tableaux de la figure 1, cette procédure affiche à l’écran :
>>> plan = [[5, 4], [1, 2, None, None, None], [3, 4, 1, 5, None], [0, None, None, None, None], [2, 2, 5, None, None], [2, 4, 2, None, None]]
>>> afficheToutesLesRoutes(plan)
Ce plan contient 4 route(s): (1-2) (2-4) (2-5) (4-5)

  • Le sujet demandait “Quelle est la complexité en temps de votre procédure dans le pire cas en fonction de n et m ?” :

    1. Complexité en temps : \(O(n^3)\) (dans le pire des cas, car on doit alors parcourir tous les couples de sommets (x, y), vérifier à chaque fois s’ils sont connectés en \(O(n)\)),
    2. Note : il me semble possible de pouvoir faire mieux, mais l’algorithme deviendrait bien plus compliqué (sans utiliser estVoisine() mais un parcours malin des listes d’adjacence),
    3. Complexité en mémoire : \(O(m)\) (on doit stocker la chaîne de caractère des m routes (i-j)).

Plan 1 :

_images/X_PSI_PT__2015__plan1.png

Plan 2 :

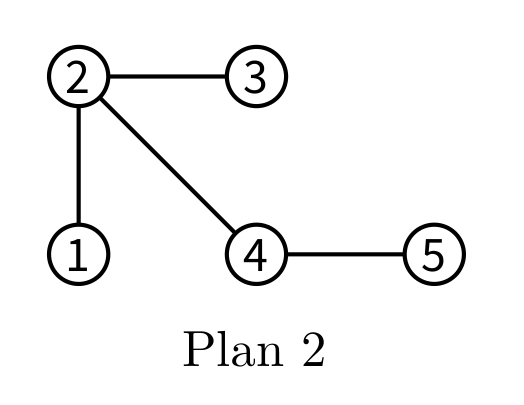
_images/X_PSI_PT__2015__plan2.png
X_PSI_PT__2015.entierAleatoire(k)[source]

(Préliminaires partie III) Renvoie un entier aléatoire uniforme entre 1 et k.

C’est à dire qu’on a \(\mathbb{P}r\{ \mathtt{entierAleatoire}(k) = c \} = 1/k\) pour tout entier \(c \in \{ 1, \dots, k \}\)), exactement comme demandé.

  • Elle n’était pas demandée, mais supposée donnée,
  • (Hypothèse) Complexité en temps : \(O(1)\) (toujours),
  • (Hypothèse) Complexité en mémoire : \(O(1)\) (toujours),
  • C’est exactement random.randint()... renommée en français.
  • Exemple :
>>> random.seed(0)  # Pas d'aléa ici, pour la reproductibilité de l'exemple
>>> entierAleatoire(10)
7
>>> entierAleatoire(2)
2
  • Hypothèse : on suppose pour cette fonction et la suite qu’on dispose d’un “bon” générateur de nombres aléatoires (PRNG, Pseudo-Random Number Generator) qui assure (mathématiquement) que ces entiers sont tous indépendants, et que les tirages sont effectivement identiquement distribués. Voir la documentation Python du module random ou cette page Wikipédia pour plus d’informations.
X_PSI_PT__2015.coloriageAleatoire(plan, couleur, k, s, t)[source]

(Question 9) Génère un coloriage aléatoire pour le plan plan.

  • Prend en argument un plan plan de n villes, un tableau couleur de taille n + 1, un entier k, et deux villes s et t (\(s,t \in \{ 1, \dots, n \}\)),
  • Remplit le tableau couleur avec une couleur aléatoire uniforme dans \{ 1, \dots, k \}, choisie indépendamment pour chaque ville \(i \in \{ 1, \dots, n \} \setminus \{s, t\}\),
  • On impose les couleurs 0 et k + 1 pour s et t respectivement,
  • La case couleur[0] n’est pas utilisée (elle reste égale à None, ou n’importe quelle valeur arbitraire).
  • Complexité en temps : \(O(n)\) (toujours),
  • Complexité en mémoire : \(O(n)\) (toujours),
  • Exemple :
>>> plan = [[5, 4], [1, 2, None, None, None], [3, 1, 3, 4, None], [1, 2, None, None, None], [2, 2, 5, None, None], [1, 4, None, None, None]]  # plan2, cf ci-dessus
>>> n = plan[0][0]
>>> couleur = creerTableau(n+1)  # Tableau vide
>>> affiche(couleur)
[None, None, None, None, None, None]
>>> k = 2; s = 1; t = 5
>>> random.seed(0)  # Pas d'aléa ici, pour la reproductibilité de l'exemple
>>> coloriageAleatoire(plan, couleur, k, s, t)
>>> affiche(couleur)
[None, 0, 2, 2, 1, 3]
X_PSI_PT__2015.voisinesDeCouleur(plan, couleur, i, c)[source]

(Question 10) Crée et renvoie un tableau codant la liste (sans redondance) des villes de couleur c voisines de la ville i dans le plan plan colorié par le tableau couleur.

  • Complexité en temps : \(O(n + m)\). On doit créer en \(O(n)\) la liste initialement vide des possibles voisines de i de couleurs c. Ensuite, pour chaque ville j voisine avec i, on doit vérifier si couleur[j] = c (en temps constant \(O(1)\)), et le nombre \(\delta(i)\) de voisines de i est un \(O(m)\), cf. estVoisine(),
  • Complexité en mémoire : \(O(n)\) (toujours),
  • Exemple :
>>> plan = [[5, 4], [1, 2, None, None, None], [3, 1, 3, 4, None], [1, 2, None, None, None], [2, 2, 5, None, None], [1, 4, None, None, None]]  # plan2, cf ci-dessus
>>> n = plan[0][0]
>>> couleur = [None, 0, 2, 2, 2, 3]  # Un coloriage
>>> i = 2
>>> c = 2
>>> affiche(voisinesDeCouleur(plan, couleur, i, c))
[2, 3, 4, None, None, None]
>>> couleur = [None, 0, 2, 1, 2, 3]  # Autre coloriage
>>> i = 4
>>> c = 3
>>> affiche(voisinesDeCouleur(plan, couleur, i, c))
[1, 5, None, None, None, None]
X_PSI_PT__2015.voisinesDeLaListeDeCouleur(plan, couleur, liste, c)[source]

(Question 11) Crée et renvoie un tableau codant la liste (sans redondance) des villes de couleur c voisines d’une des villes présente dans la liste (sans redondance) liste dans le plan plan colorié par le tableau couleur.

  • Cette seconde fonction semble compliquée, mais c’est simplement une union sur les \(i \in \mathtt{liste}\) des voisinesDeCouleur(plan, couleur, i, c) donnée par la fonction d’avant !
  • Complexité en temps : \(O(\# liste \times (n + m))\) (pour chaque ville k de la liste liste, on appelle la fonction précédente voisinesDeCouleur(), qui est en temps \(O(n + m)\)),
  • Complexité en mémoire : \(O(n)\) (toujours),
  • Exemple :
>>> plan = [[5, 4], [1, 2, None, None, None], [3, 1, 3, 4, None], [1, 2, None, None, None], [2, 2, 5, None, None], [1, 4, None, None, None]]  # plan2, cf ci-dessus
>>> n = plan[0][0]
>>> couleur = [None, 0, 2, 2, 1, 3]  # Un coloriage
>>> liste = creerListeVide(n+1)  # liste = {} ensemble vide
>>> ajouteDansListe(liste, 1)  # liste = {1}
>>> ajouteDansListe(liste, 2)  # liste = {1, 2}
>>> c = 2
>>> affiche(voisinesDeLaListeDeCouleur(plan, couleur, liste, c))
[2, 2, 3, None, None, None]
  • Dans ces deux exemples, on regarde tous les voisines de 1 ou de 2 (en fait, liste représente l’ensemble \(\{1,2\}\)), et on affiche ceux de couleur c = 2 (soit 2 comme voisine de 1 et 3 comme voisine de 2),
  • Et ci-dessous, on affiche les voisines de 1 ou de 2 qui sont de couleur c = 1 (soit uniquement 4 comme voisine de 2).
>>> c = 1
>>> affiche(voisinesDeLaListeDeCouleur(plan, couleur, liste, c))
[1, 4, None, None, None, None]
_images/X_PSI_PT__2015__plan2.png
X_PSI_PT__2015.existeCheminArcEnCiel(plan, couleur, k, s, t)[source]

(Question 12) Renvoie True s’il existe dans le plan plan, un chemin \(s \sim v_1 \sim \dots \sim v_k \sim t\), tel que \(\mathtt{couleur}[v_j] = j\) pour tout \(j \in \{ 1, \dots, k\}\), et renvoie False sinon.

  • L’objectif de cette partie est d’écrire une procédure qui détermine s’il existe un chemin de longueur k + 2, allant de s à t, dont la j-ème ville intermédiaire a reçu la couleur j.
  • Complexité en temps : \(O(n (n+m))\). On fait des appels à la fonction précédente voisinesDeLaListeDeCouleur() (qui était en \(O(n+m)\)) avec des listes liste de tailles variables, mais dont la somme ne sera pas plus que le nombre de villes n (en effet une ville ne peut être qu’une seule fois dans une liste). (C’est ce qu’on appelle une complexité cumulée.)
  • Complexité en mémoire : \(O(n)\) (toujours).
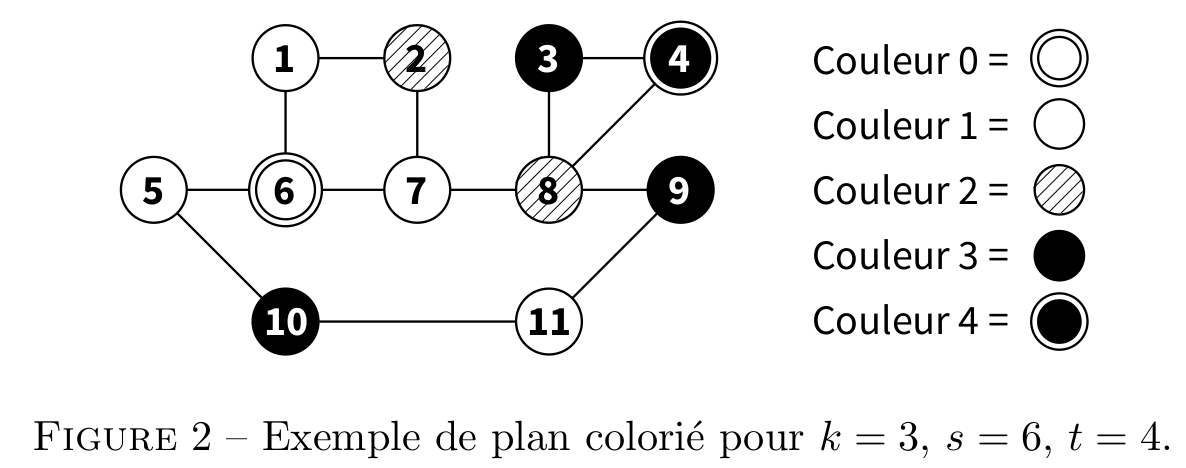
_images/X_PSI_PT__2015__plan3.png
  • Premier exemple, avec le plan de la figure 2, qui trouve un chemin arc-en-ciel (de taille k = 3) entre s = 6 et t = 4 : \(6 \sim 7 \sim 8 \sim 3 \sim 4\) :
>>> plan = [[11, 13], [2, 2, 6], [2, 1, 7], [2, 4, 8], [2, 3, 8], [2, 6, 10], [3, 1, 5, 7], [3, 2, 6, 8], [4, 3, 4, 7, 9], [2, 8, 11], [2, 5, 11], [2, 9, 10]]
>>> s = 6
>>> t = 4
>>> k = 3
>>> couleur = [None, 1, 2, 3, k+1, 1, 0, 1, 2, 3, 3, 1]
>>> affiche(existeCheminArcEnCiel(plan, couleur, k, s, t))
True
  • Le même exemple mais dans l’autre sens, qui trouve un chemin arc-en-ciel (de taille k = 3) entre s = 4 et t = 6 : \(4 \sim 3 \sim 8 \sim 7 \sim 6\) :
>>> plan = [[11, 13], [2, 2, 6], [2, 1, 7], [2, 4, 8], [2, 3, 8], [2, 6, 10], [3, 1, 5, 7], [3, 2, 6, 8], [4, 3, 4, 7, 9], [2, 8, 11], [2, 5, 11], [2, 9, 10]]
>>> s = 4
>>> t = 6
>>> k = 3
>>> couleur = [None, 3, 2, 1, 0, 3, k+1, 3, 2, 1, 1, 3]
>>> affiche(existeCheminArcEnCiel(plan, couleur, k, s, t))
True
  • Un autre exemple similaire, qui trouve un aussi chemin arc-en-ciel (de taille k = 3), entre s = 11 et t = 7 : \(11 \sim 10 \sim 5 \sim 6 \sim 7\) :
>>> plan = [[11, 13], [2, 2, 6], [2, 1, 7], [2, 4, 8], [2, 3, 8], [2, 6, 10], [3, 1, 5, 7], [3, 2, 6, 8], [4, 3, 4, 7, 9], [2, 8, 11], [2, 5, 11], [2, 9, 10]]
>>> s = 11
>>> t = 7
>>> k = 3
>>> couleur = [None, 1, 2, 3, 3, 2, 3, k+1, 2, 1, 1, 0]
>>> affiche(existeCheminArcEnCiel(plan, couleur, k, s, t))
True
  • Un autre exemple similaire, qui trouve un aussi chemin arc-en-ciel (de taille k = 2), entre s = 11 et t = 7 : \(11 \sim 9 \sim 8 \sim 7\) :
>>> plan = [[11, 13], [2, 2, 6], [2, 1, 7], [2, 4, 8], [2, 3, 8], [2, 6, 10], [3, 1, 5, 7], [3, 2, 6, 8], [4, 3, 4, 7, 9], [2, 8, 11], [2, 5, 11], [2, 9, 10]]
>>> s = 11
>>> t = 7
>>> k = 2
>>> couleur = [None, 1, 2, 3, 3, 2, 3, k+1, 2, 1, 1, 0]
>>> affiche(existeCheminArcEnCiel(plan, couleur, k, s, t))
True
  • Un autre exemple similaire, qui ne pas trouve de chemin arc-en-ciel (de taille k = 3), car le coloriage est “mauvais” :
>>> plan = [[11, 13], [2, 2, 6], [2, 1, 7], [2, 4, 8], [2, 3, 8], [2, 6, 10], [3, 1, 5, 7], [3, 2, 6, 8], [4, 3, 4, 7, 9], [2, 8, 11], [2, 5, 11], [2, 9, 10]]
>>> s = 11
>>> t = 7
>>> k = 3
>>> couleur = [None, 1, 2, 3, 3, 2, 3, k+1, 2, 1, 1, 0]
>>> # On change la couleur de la ville 6 (qui était dans le chemin arc-en-ciel précédent)
>>> couleur[6] = 1
>>> affiche(existeCheminArcEnCiel(plan, couleur, k, s, t))
False
  • Notez que le graphe étant complet, il y a toujours un chemin entre s et t, mais pas forcément de chemin arc-en-ciel pour un certains k, et couleur.
X_PSI_PT__2015.existeCheminSimple(plan, k, s, t)[source]

(Question 13) Renvoie True avec probabilité au moins \(1 - 1/e\) s’il existe un chemin de s à t passant par exactement k villes intermédiaires toutes distinctes dans le plan plan, et renvoie toujours False sinon.

  • Exécute \(k^k\) fois la fonction existeCheminArcEnCiel() et renvoie True dès qu’une de ses exécution a trouvé un coloriage (aléatoire) qui permet de trouver un chemin “arc-en-ciel”.
  • Complexité en temps : \(O(k^k n (n+m))\). Dans le pire des cas on fait \(k^k = \mathtt{nombre\_executions}\) essais avec existeCheminArcEnCiel() qui est en temps \(O(n (n+m))\) (et générer un coloriage est en temps \(O(n)\) donc négligeable),
  • Note : c’est bien la complexité annoncée, avec \(f(k) = k^k\) (le nombre d’essai, dépandant uniquement de k) et \(g(n,m) = n (n+m)\) (la taille du plan).
  • Complexité en mémoire : \(O(n)\) (toujours).

Avertissement

C’est un algorithme probabiliste !

Il faut garder en tête que cette fonction n’est pas exacte mais probabiliste (on parle aussi d’un algorithme randomisé, et c’est un sujet à part entière, voir cette page par exemple ou celle-là) :

  • Si elle dit True, c’est qu’il existe un chemin, et on en est sûr (voir la question d’après pour en trouver un, on dit alors qu’on fournit un certificat de réponse), et ça a pris au plus \(O(k^k n (n+m))\),
  • Si elle dit False, c’est peut-être vrai, avec une bonne probabilité, mais aucune garantie 100% (et ça a pris exactement \(O(k^k n (n+m))\)).
  • S’il existe un chemin, on a une bonne probabilité de le trouver (mais si on le trouve pas ce n’est pas une garantie qu’il n’y en a pas),
  • S’il n’y a pas de chemin, on a une bonne probabilité de répondre False (mais jamais une garantie qu’il n’y en a pas).
_images/X_PSI_PT__2015__plan3.png
  • Un exemple, avec le plan de la figure 2, qui va trouver un chemin arc-en-ciel (de taille k = 3) entre s = 6 et t = 4 : \(6 \sim 7 \sim 8 \sim 3 \sim 4\). On peut donc faire confiance à 100% à cette réponse positive !
>>> plan = [[11, 13], [2, 2, 6], [2, 1, 7], [2, 4, 8], [2, 3, 8], [2, 6, 10], [3, 1, 5, 7], [3, 2, 6, 8], [4, 3, 4, 7, 9], [2, 8, 11], [2, 5, 11], [2, 9, 10]]
>>> s = 6
>>> t = 4
>>> k = 3
>>> random.seed(0)  # Pas d'aléa ici, pour la reproductibilité de l'exemple
>>> # Ca peut prendre du temps...
>>> affiche(existeCheminSimple(plan, k, s, t))
True
>>> # Mais on n'est pas sûr de cette réponse !
  • Un deuxième exemple, avec un plan légèrement modifié inspiré de celui de la figure 2, où on enlève le lien \(8 \sim 3\), et donc on ne trouvra pas un chemin arc-en-ciel (de taille k = 3) entre s = 6 et t = 4. Notez qu’avec cette méthode, on ne peut pas faire confiance à 100% à cette réponse négative !
>>> plan = [[11, 12], [2, 2, 6], [2, 1, 7], [1, 4], [2, 3, 8], [2, 6, 10], [3, 1, 5, 7], [3, 2, 6, 8], [3, 4, 7, 9], [2, 8, 11], [2, 5, 11], [2, 9, 10]]
>>> s = 6
>>> t = 4
>>> k = 3
>>> random.seed(0)  # Pas d'aléa ici, pour la reproductibilité de l'exemple
>>> # Ca peut prendre du temps...
>>> affiche(existeCheminSimple(plan, k, s, t))
False
>>> # Mais on n'est pas sûr de cette réponse !
  • Hypothèse : on dispose d’un bon générateur de nombres aléatoires (PRNG, Pseudo-Random Number Generator) qui assure mathématiquement que ces exécutions sont toutes indépendantes, et que les coloriages sont effectivement uniformément distribués. Voir la documentation Python du module random ou cette page Wikipédia pour plus d’informations.
X_PSI_PT__2015.question14()[source]

(Question 14) Le programme à modifier est existeCheminArcEnCiel. En un mot : il faut faire en sorte de garder en mémoire les listes liste successives.

Plus de détails :

  • Voici une solution possible pour calculer le chemin, plus détaillée : utiliser un tableau des prédécesseurs pred, permettant de reconstituer le chemin a posteriori.
  • Plus précisément : on utilise un tableau pred à n cases tel que pour toute ville x, pred[x] est le numéro d’une ville y reliée à x et qui précède x dans un éventuel chemin de s `` à ``t.
  • Ce tableau est créé et complété au fur et à mesure par la fonction existeCheminArcEnCiel() : lors de chaque appel à la fonction auxiliaire voisinesDeLaListeDeCouleur() appliquée (plan, couleur, liste, j) on met à jour le tableau pred : pour chaque ville x de couleur j voisine d’une ville y de la liste, on affecte pred[x] = y (il y a une route de y à x, et si le chemin passe par x, il sera passé par y juste avant). (pour cela, on ajoute le tableau pred dans les arguments de la fonction auxiliaire voisinesDeLaListeDeCouleur() et celle-ci effectue elle-même la mise à jour, en même temps qu’elle calcule la nouvelle liste de voisines).
  • À la fin, si un chemin est détecté, on le reconstitue en partant de la fin (c’est classique) grâce au tableau pred : pred[t] = y1, pred[y1] = y2, pred[y2] = y3, etc, jusqu’à retomber sur s : pred[yk] = s, alors le chemin est s -> yk -> ... -> y2 -> y1 -> t (ce chemin est de longueur k+2 par construction).

Note

Exemple avec le plan de la figure 2 :

  • À la 1e étape, liste contient 1, 5, 7 (les voisins de s=6 de couleur 1), on affecte pred[1] = pred[5] = pred[7] = 6.
  • À la 2e étape, liste contient 2, 8 (les voisins de 1, 5, 7 de couleur 2), on affecte pred[2] = 1 (ou 7 au choix), pred[8] = 7.
  • À la 3e étape, liste contient 3, 9, on affecte pred[3] = pred[9] = 8.
  • À la 4e étape, liste contient 4, on affecte pred[4] = 3.

Pour notre exemple : en partant de la fin (t=4) on a pred[4] = 3, pred[3] = 8, pred[8] = 7, pred[7] = 6 le chemin reconstitué est 6 -> 7 -> 8 -> 3 -> 4, et on peut vérifier sur le plan de la figure 2 que c’est bien un chemin valide :

_images/X_PSI_PT__2015__plan3.png

Note

Cette fonction ne fait rien, elle donne juste la correction de la dernière question (14) du DS.

Conseils

  • Améliorez la présentation de vos copies,
  • Essayez d’être encore plus attentif à la syntaxe de Python (il y a eu trop d’erreurs d’indentation et de : manquants),
  • Vous devez être plus attentif aux consignes de l’énoncé (certains élèves oublient de donner la complexité dans les dernières questions),
  • Comme dans chaque concours/DS, vous devez essayer de “grapiller” des points là où vous peuvez (la Q09 (X_PSI_PT__2015.coloriageAleatoire()) et Q13 (X_PSI_PT__2015.existeCheminSimple()) étaient faciles, par exemple),
  • Enfin, vous devez vous forcer à n’utiliser que les structures de données de l’énoncé (c’est flagrant, certains commencent par utiliser X_PSI_PT__2015.creerTableau() ou X_PSI_PT__2015.creerListeVide() au début, puis finissent avec des [] et list.append() à tout va), probablement par manque de concentration et à cause de la fatigue.

Sortie du script

$ python3 X_PSI_PT__2015.py
 Correction du DS de vendredi 11 décembre 2015.

Voici ci-dessous la documentation de la correction complète du sujet d'écrit d'informatique (Polytechnique et ENS, 2015), pour PSI et PT.

Ce sujet d'écrit a été posé en devoir écrit surveillé (DS) pour le cours d'informatique pour tous en prépa MP au Lycée Lakanal.


Veuillez `consulter le code source pour tous les détails <_modules/X_PSI_PT__2015__minimal_solution.html>`_ svp.
Ci dessous se trouve simplement la *documentation* de ce programme.


- *Date :* Vendredi 11 décembre 2015,
- *Auteur :* Lilian Besson, pour le cours d'informatique pour tous en prépa MP (http://perso.crans.org/besson/infoMP/),
- *Licence :* MIT Licence (http://lbesson.mit-license.org).


.. note::

   Cette correction contient beaucoup de documentation, des exemples et des détails.
   Pour une correction beaucoup plus concise, voir `cette page <_modules/X_PSI_PT__2015__minimal_solution.html>`_.

.. warning::

   Les fonctions sont ici listées par ordre alphabétique, et pas dans l'ordre du fichier source.
   D'habitude, j'arrive à `corriger ça <http://sphinx-doc.org/ext/autodoc.html#confval-autodoc_member_order>`_, mais là non. Désolé.
   Je trouverai comment régler ce problème !



Partie 0 : Fonctions supposées données


Partie I : Préliminaires : Listes dans redondance
Note : une liste non-ordonnée et sans redondance est exactement un set de Python, mais nous ne devons pas nous en servir.


Partie II. Création et manipulation de plans
Plan de la figure 1 :
plan0 = [[5, 4],
         [1, 2, None, None, None],
         [3, 4, 1, 5, None],
         [0, None, None, None, None],
         [2, 2, 5, None, None],
         [2, 4, 2, None, None],
         ]

[[5, 4], [1, 2, None, None, None], [3, 4, 1, 5, None], [0, None, None, None, None], [2, 2, 5, None, None], [2, 4, 2, None, None]]
Premier plan :
plan1 = [[5, 7],
         [2, 2, 3, None, None],
         [3, 1, 3, 5, None],
         [4, 1, 2, 4, 5],
         [2, 3, 5, None, None],
         [3, 2, 3, 4, None],
         ]

[[5, 7], [2, 2, 3, None, None], [3, 1, 3, 5, None], [4, 1, 2, 4, 5], [2, 3, 5, None, None], [3, 2, 3, 4, None]]
Deuxième plan :
plan2 = [[5, 4],
         [1, 2, None, None, None],
         [3, 1, 3, 4, None],
         [1, 2, None, None, None],
         [2, 2, 5, None, None],
         [1, 4, None, None, None],
         ]

[[5, 4], [1, 2, None, None, None], [3, 1, 3, 4, None], [1, 2, None, None, None], [2, 2, 5, None, None], [1, 4, None, None, None]]
Partie III. Recherche de chemins arc-en-ciel
Plan de la figure 2 :
plan3 = [[11, 13],
         [2, 2, 6],
         [2, 1, 7],
         [2, 4, 8],
         [2, 3, 8],
         [2, 6, 10],
         [3, 1, 5, 7],
         [3, 2, 6, 8],
         [4, 3, 4, 7, 9],
         [2, 8, 11],
         [2, 5, 11],
         [2, 9, 10],
         ]

[[11, 13], [2, 2, 6, None, None, None, None, None, None, None, None, None], [2, 1, 7, None, None, None, None, None, None, None, None, None], [2, 4, 8, None, None, None, None, None, None, None, None, None], [2, 3, 8, None, None, None, None, None, None, None, None, None], [2, 6, 10, None, None, None, None, None, None, None, None, None], [3, 2, 6, 8, None, None, None, None, None, None, None, None], [3, 1, 5, 7, None, None, None, None, None, None, None, None], [4, 3, 4, 7, 9, None, None, None, None, None, None, None], [2, 8, 11, None, None, None, None, None, None, None, None, None], [2, 5, 11, None, None, None, None, None, None, None, None, None], [2, 9, 10, None, None, None, None, None, None, None, None, None]]
Ce plan contient 13 route(s): (1-2) (3-4) (3-8) (4-8) (5-10) (8-9) (9-11) (10-11)
Partie IV. Recherche de chemin passant par exactement k villes intermédiaires distinctes
Test automatique de toutes les doctests écrites dans la documentation (docstring) de chaque fonction :
Trying:
    x = 1; y = x+1
Expecting nothing
ok
Trying:
    affiche("x = ",x," et y = ",y)
Expecting:
    x = 1 et y = 2
ok
Trying:
    plan = [[5, 4], [1, 2, None, None, None], [3, 4, 1, 5, None], [0, None, None, None, None], [2, 2, 5, None, None], [2, 4, 2, None, None]]
Expecting nothing
ok
Trying:
    afficheToutesLesRoutes(plan)
Expecting:
    Ce plan contient 4 route(s): (1-2) (2-4) (2-5) (4-5)
ok
Trying:
    n = 5; liste = creerListeVide(n)
Expecting nothing
ok
Trying:
    for i in range(1, n+1):
        ajouteDansListe(liste, 4**i)
Expecting nothing
ok
Trying:
    affiche(liste)
Expecting:
    [5, 4, 16, 64, 256, 1024]
ok
Trying:
    ensemble = { 4**i for i in range(1, n+1)}
Expecting nothing
ok
Trying:
    affiche(ensemble)  # L'ordre est arbitraire ! set([16, 64, 4, 256, 1024])
Expecting:
    {16, 64, 256, 1024, 4}
**********************************************************************
File "X_PSI_PT__2015.py", line 165, in __main__.ajouteDansListe
Failed example:
    affiche(ensemble)  # L'ordre est arbitraire ! set([16, 64, 4, 256, 1024])
Expected:
    {16, 64, 256, 1024, 4}
Got:
    {16, 256, 64, 4, 1024}
Trying:
    ajouteDansListe(liste, 2015)
Expecting:
    Impossible d'ajouter l'élément x = 2015 à la liste [5, 4, 16, 64, 256, 1024] qui est déjà pleine (n = 5).
ok
Trying:
    plan = [[5, 4], [1, 2, None, None, None], [3, 1, 3, 4, None], [1, 2, None, None, None], [2, 2, 5, None, None], [1, 4, None, None, None]]  # plan2, cf ci-dessus
Expecting nothing
ok
Trying:
    affiche("Ce plan a m = ", plan[0][1], " route(s).")
Expecting:
    Ce plan a m = 4 route(s).
ok
Trying:
    x = 1; y = 5
Expecting nothing
ok
Trying:
    affiche(estVoisine(plan, x, y))
Expecting:
    False
ok
Trying:
    ajouteRoute(plan, x, y)
Expecting nothing
ok
Trying:
    affiche("Ce plan a m = ", plan[0][1], " route(s).")
Expecting:
    Ce plan a m = 5 route(s).
ok
Trying:
    affiche(estVoisine(plan, x, y))
Expecting:
    True
ok
Trying:
    plan = [[5, 4], [1, 2, None, None, None], [3, 1, 3, 4, None], [1, 2, None, None, None], [2, 2, 5, None, None], [1, 4, None, None, None]]  # plan2, cf ci-dessus
Expecting nothing
ok
Trying:
    n = plan[0][0]
Expecting nothing
ok
Trying:
    couleur = creerTableau(n+1)  # Tableau vide
Expecting nothing
ok
Trying:
    affiche(couleur)
Expecting:
    [None, None, None, None, None, None]
ok
Trying:
    k = 2; s = 1; t = 5
Expecting nothing
ok
Trying:
    random.seed(0)  # Pas d'aléa ici, pour la reproductibilité de l'exemple
Expecting nothing
ok
Trying:
    coloriageAleatoire(plan, couleur, k, s, t)
Expecting nothing
ok
Trying:
    affiche(couleur)
Expecting:
    [None, 0, 2, 2, 1, 3]
ok
Trying:
    n = 5; liste = creerListeVide(n)
Expecting nothing
ok
Trying:
    affiche(liste)
Expecting:
    [0, None, None, None, None, None]
ok
Trying:
    n = 4; plan = creerPlanSansRoute(n)
Expecting nothing
ok
Trying:
    affiche(plan)
Expecting:
    [[4, 0], [0, None, None, None, None, None], [0, None, None, None, None, None], [0, None, None, None, None, None], [0, None, None, None, None, None]]
ok
Trying:
    n = 5; t = creerTableau(n)
Expecting nothing
ok
Trying:
    for i in range(n):
        t[i] = i + 2
Expecting nothing
ok
Trying:
    affiche(t)
Expecting:
    [2, 3, 4, 5, 6]
ok
Trying:
    p = 2; q = 2;
Expecting nothing
ok
Trying:
    a = creerTableau2D(p, q)
Expecting nothing
ok
Trying:
    for i in range(p):
        for j in range(q):
            a[i][j] = i+j
Expecting nothing
ok
Trying:
    affiche(a)
Expecting:
    [[0, 1], [1, 2]]
ok
Trying:
    random.seed(0)  # Pas d'aléa ici, pour la reproductibilité de l'exemple
Expecting nothing
ok
Trying:
    entierAleatoire(10)
Expecting:
    7
ok
Trying:
    entierAleatoire(2)
Expecting:
    2
ok
Trying:
    liste = [5, 5, 4, 2, 1, 3]
Expecting nothing
ok
Trying:
    affiche(estDansListe(liste, 0))
Expecting:
    False
ok
Trying:
    affiche(estDansListe(liste, 5))
Expecting:
    True
ok
Trying:
    affiche(estDansListe(liste, 194652))
Expecting:
    False
ok
Trying:
    plan = [[5, 4], [1, 2, None, None, None], [3, 1, 3, 4, None], [1, 2, None, None, None], [2, 2, 5, None, None], [1, 4, None, None, None]]  # plan2, cf ci-dessus
Expecting nothing
ok
Trying:
    x = 1; y = 2
Expecting nothing
ok
Trying:
    affiche(estVoisine(plan, x, y))
Expecting:
    True
ok
Trying:
    x = 1; y = 5
Expecting nothing
ok
Trying:
    affiche(estVoisine(plan, x, y))
Expecting:
    False
ok
Trying:
    plan = [[11, 13], [2, 2, 6], [2, 1, 7], [2, 4, 8], [2, 3, 8], [2, 6, 10], [3, 1, 5, 7], [3, 2, 6, 8], [4, 3, 4, 7, 9], [2, 8, 11], [2, 5, 11], [2, 9, 10]]
Expecting nothing
ok
Trying:
    s = 6
Expecting nothing
ok
Trying:
    t = 4
Expecting nothing
ok
Trying:
    k = 3
Expecting nothing
ok
Trying:
    couleur = [None, 1, 2, 3, k+1, 1, 0, 1, 2, 3, 3, 1]
Expecting nothing
ok
Trying:
    affiche(existeCheminArcEnCiel(plan, couleur, k, s, t))
Expecting:
    True
ok
Trying:
    plan = [[11, 13], [2, 2, 6], [2, 1, 7], [2, 4, 8], [2, 3, 8], [2, 6, 10], [3, 1, 5, 7], [3, 2, 6, 8], [4, 3, 4, 7, 9], [2, 8, 11], [2, 5, 11], [2, 9, 10]]
Expecting nothing
ok
Trying:
    s = 4
Expecting nothing
ok
Trying:
    t = 6
Expecting nothing
ok
Trying:
    k = 3
Expecting nothing
ok
Trying:
    couleur = [None, 3, 2, 1, 0, 3, k+1, 3, 2, 1, 1, 3]
Expecting nothing
ok
Trying:
    affiche(existeCheminArcEnCiel(plan, couleur, k, s, t))
Expecting:
    True
ok
Trying:
    plan = [[11, 13], [2, 2, 6], [2, 1, 7], [2, 4, 8], [2, 3, 8], [2, 6, 10], [3, 1, 5, 7], [3, 2, 6, 8], [4, 3, 4, 7, 9], [2, 8, 11], [2, 5, 11], [2, 9, 10]]
Expecting nothing
ok
Trying:
    s = 11
Expecting nothing
ok
Trying:
    t = 7
Expecting nothing
ok
Trying:
    k = 3
Expecting nothing
ok
Trying:
    couleur = [None, 1, 2, 3, 3, 2, 3, k+1, 2, 1, 1, 0]
Expecting nothing
ok
Trying:
    affiche(existeCheminArcEnCiel(plan, couleur, k, s, t))
Expecting:
    True
ok
Trying:
    plan = [[11, 13], [2, 2, 6], [2, 1, 7], [2, 4, 8], [2, 3, 8], [2, 6, 10], [3, 1, 5, 7], [3, 2, 6, 8], [4, 3, 4, 7, 9], [2, 8, 11], [2, 5, 11], [2, 9, 10]]
Expecting nothing
ok
Trying:
    s = 11
Expecting nothing
ok
Trying:
    t = 7
Expecting nothing
ok
Trying:
    k = 2
Expecting nothing
ok
Trying:
    couleur = [None, 1, 2, 3, 3, 2, 3, k+1, 2, 1, 1, 0]
Expecting nothing
ok
Trying:
    affiche(existeCheminArcEnCiel(plan, couleur, k, s, t))
Expecting:
    True
ok
Trying:
    plan = [[11, 13], [2, 2, 6], [2, 1, 7], [2, 4, 8], [2, 3, 8], [2, 6, 10], [3, 1, 5, 7], [3, 2, 6, 8], [4, 3, 4, 7, 9], [2, 8, 11], [2, 5, 11], [2, 9, 10]]
Expecting nothing
ok
Trying:
    s = 11
Expecting nothing
ok
Trying:
    t = 7
Expecting nothing
ok
Trying:
    k = 3
Expecting nothing
ok
Trying:
    couleur = [None, 1, 2, 3, 3, 2, 3, k+1, 2, 1, 1, 0]
Expecting nothing
ok
Trying:
    couleur[6] = 1
Expecting nothing
ok
Trying:
    affiche(existeCheminArcEnCiel(plan, couleur, k, s, t))
Expecting:
    False
ok
Trying:
    plan = [[11, 13], [2, 2, 6], [2, 1, 7], [2, 4, 8], [2, 3, 8], [2, 6, 10], [3, 1, 5, 7], [3, 2, 6, 8], [4, 3, 4, 7, 9], [2, 8, 11], [2, 5, 11], [2, 9, 10]]
Expecting nothing
ok
Trying:
    s = 6
Expecting nothing
ok
Trying:
    t = 4
Expecting nothing
ok
Trying:
    k = 3
Expecting nothing
ok
Trying:
    random.seed(0)  # Pas d'aléa ici, pour la reproductibilité de l'exemple
Expecting nothing
ok
Trying:
    affiche(existeCheminSimple(plan, k, s, t))
Expecting:
    True
ok
Trying:
    plan = [[11, 12], [2, 2, 6], [2, 1, 7], [1, 4], [2, 3, 8], [2, 6, 10], [3, 1, 5, 7], [3, 2, 6, 8], [3, 4, 7, 9], [2, 8, 11], [2, 5, 11], [2, 9, 10]]
Expecting nothing
ok
Trying:
    s = 6
Expecting nothing
ok
Trying:
    t = 4
Expecting nothing
ok
Trying:
    k = 3
Expecting nothing
ok
Trying:
    random.seed(0)  # Pas d'aléa ici, pour la reproductibilité de l'exemple
Expecting nothing
ok
Trying:
    affiche(existeCheminSimple(plan, k, s, t))
Expecting:
    False
ok
Trying:
    plan = [[5, 4], [1, 2, None, None, None], [3, 1, 3, 4, None], [1, 2, None, None, None], [2, 2, 5, None, None], [1, 4, None, None, None]]  # plan2, cf ci-dessus
Expecting nothing
ok
Trying:
    n = plan[0][0]
Expecting nothing
ok
Trying:
    couleur = [None, 0, 2, 2, 2, 3]  # Un coloriage
Expecting nothing
ok
Trying:
    i = 2
Expecting nothing
ok
Trying:
    c = 2
Expecting nothing
ok
Trying:
    affiche(voisinesDeCouleur(plan, couleur, i, c))
Expecting:
    [2, 3, 4, None, None, None]
ok
Trying:
    couleur = [None, 0, 2, 1, 2, 3]  # Autre coloriage
Expecting nothing
ok
Trying:
    i = 4
Expecting nothing
ok
Trying:
    c = 3
Expecting nothing
ok
Trying:
    affiche(voisinesDeCouleur(plan, couleur, i, c))
Expecting:
    [1, 5, None, None, None, None]
ok
Trying:
    plan = [[5, 4], [1, 2, None, None, None], [3, 1, 3, 4, None], [1, 2, None, None, None], [2, 2, 5, None, None], [1, 4, None, None, None]]  # plan2, cf ci-dessus
Expecting nothing
ok
Trying:
    n = plan[0][0]
Expecting nothing
ok
Trying:
    couleur = [None, 0, 2, 2, 1, 3]  # Un coloriage
Expecting nothing
ok
Trying:
    liste = creerListeVide(n+1)  # liste = {} ensemble vide
Expecting nothing
ok
Trying:
    ajouteDansListe(liste, 1)  # liste = {1}
Expecting nothing
ok
Trying:
    ajouteDansListe(liste, 2)  # liste = {1, 2}
Expecting nothing
ok
Trying:
    c = 2
Expecting nothing
ok
Trying:
    affiche(voisinesDeLaListeDeCouleur(plan, couleur, liste, c))
Expecting:
    [2, 2, 3, None, None, None]
ok
Trying:
    c = 1
Expecting nothing
ok
Trying:
    affiche(voisinesDeLaListeDeCouleur(plan, couleur, liste, c))
Expecting:
    [1, 4, None, None, None, None]
ok
2 items had no tests:
    __main__
    __main__.question14
15 items passed all tests:
   2 tests in __main__.affiche
   2 tests in __main__.afficheToutesLesRoutes
   7 tests in __main__.ajouteRoute
   8 tests in __main__.coloriageAleatoire
   2 tests in __main__.creerListeVide
   2 tests in __main__.creerPlanSansRoute
   3 tests in __main__.creerTableau
   4 tests in __main__.creerTableau2D
   3 tests in __main__.entierAleatoire
   4 tests in __main__.estDansListe
   5 tests in __main__.estVoisine
  31 tests in __main__.existeCheminArcEnCiel
  12 tests in __main__.existeCheminSimple
  10 tests in __main__.voisinesDeCouleur
  10 tests in __main__.voisinesDeLaListeDeCouleur
**********************************************************************
1 items had failures:
   1 of   6 in __main__.ajouteDansListe
111 tests in 18 items.
110 passed and 1 failed.
***Test Failed*** 1 failures.
**********************************************************************
File "X_PSI_PT__2015.py", line 165, in __main__.ajouteDansListe
Failed example:
    affiche(ensemble)  # L'ordre est arbitraire ! set([16, 64, 4, 256, 1024])
Expected:
    {16, 64, 256, 1024, 4}
Got:
    {16, 256, 64, 4, 1024}
**********************************************************************
1 items had failures:
   1 of   6 in __main__.ajouteDansListe
***Test Failed*** 1 failures.

Plus de détails sur ces doctests sont dans la documentation de Python:
https://docs.python.org/3/library/doctest.html (en anglais)

Le fichier Python se trouve ici : X_PSI_PT__2015.py.