
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Appliquons le principe fondamental de la dynamique à un ressort horizontal de masse m et de raideur k. On écarte la masse accrochée au ressort d'une distance xo puis on lâche cette masse. Instinctivement, on sait que le ressort oscille autour de sa position de repos avant de finalement s'arrêter. Que donnent les calculs? Le système que l'on étudie est la masse m accrochée au ressort dans le référentiel terrestre supposé Galiléen. La masse du ressort est négligeable.
|
Le ressort est libre d'effort dans sa position initiale:

On écarte le ressort de sa position initiale, une force de tension T apparaît. Elle a tendance à vouloir faire revenir le ressort vers sa position initiale.

Calculs:
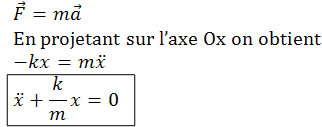
Ceci est l'équation différentielle régissant le mouvement de la masse accrochée au ressort.
.jpg)
L'équation admet une unique solution en déplacement si l'on fixe deux valeurs initiales :
- La vitesse à l'instant initial est nulle
- La position initiale du ressort est xo


Remarque 1 : Nous avons supposé ici que l'objet était suffisamment dense pour concentrer sa masse en un seul point: son centre de gravité. Dans ce cas, tous les efforts sont appliquées en ce point.
Remarque 2 : Nous n'avons pas tenu compte ici du frottement de l'air, et du frottement entre la masse et le support sur lequel il est posé. On appelle ces frottements des phénomènes diffusifs. C'est pourquoi la solution de notre calcul indique que le ressort oscille jusqu'à l'infini, tandis qu'en réalité il s'arrête au bout d'un temps, freiné par les frottements.
Remarque 3 : (important pour la suite)
Le système ne dispose que d'un seul degré de liberté: la distance x.

Que se passe t-il dans les mêmes conditions alors que l'on exerce en plus une force sinusoïdale sur le ressort? A quelle fréquence cette force va faire osciller le ressort avec la plus grande amplitude?
Pour répondre à cette question posons la force F suivante:

On remarque que si w=wF on obtient une solution qui diverge vers l'infini.
Pour mieux analyser ce résultat, observons les courbes obtenues en faisant varier la fréquence wF de la force appliquée :
![]()
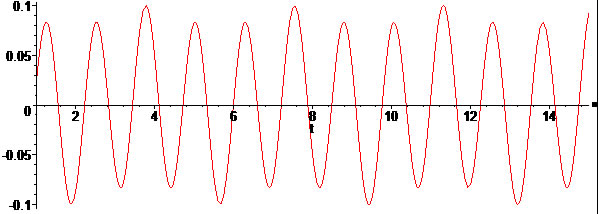
![]()

![]() On remarque que la solution atteint une amplitude très grande, il y a un phénomène de résonance qui apparait ici.
On remarque que la solution atteint une amplitude très grande, il y a un phénomène de résonance qui apparait ici.
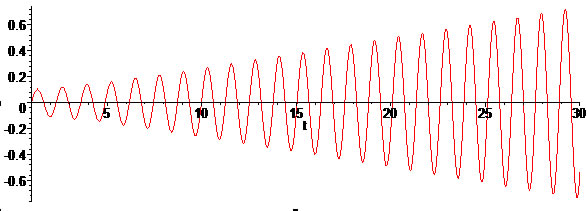
Et enfin, la même courbe mais avec une échelle plus grande, qui montre que wF est très proche de w mais n'est pas égale. En effet, si wF=w, la solution diverge vers l'infini.
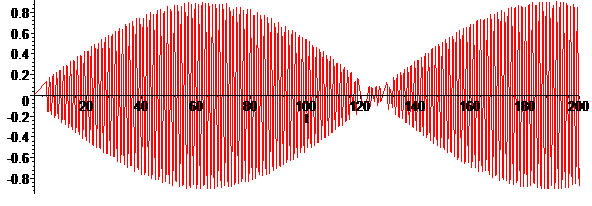
![]()

