#!/usr/bin/env python
# coding: utf-8
# # Using Python to solve Regexp CrossWord Puzzles
#
# Have a look at the amazing website.
#
# I played during about two hours, and could manually solve almost all problems, quite easily for most of them.
# But then I got stucked on [this one](https://regexcrossword.com/challenges/volapuk/puzzles/5).
#
# Soooooo. I want to use [Python3](https://docs.python.org/3/) [regular expressions](https://docs.python.org/3/library/re.html) and try to solve any such cross-word puzzles.
#
# **Warning:** This notebook will *not* explain the concept and syntax of regular expressions, go read on about it on Wikipedia or in a good book. The Python documentation gives a nice introduction [here](https://docs.python.org/3/howto/regex.html#regex-howto).
#
# - Author: [Lilian Besson](https://besson.link) ([@Naereen](https://GitHub.com/Naereen)) ;
# - License: [MIT License](https://lbesson.mit-license.org/) ;
# - Date: 28-02-2021.
# ## Representation of a problem
#
# Here is a screenshot from the game webpage.
#
# 
#
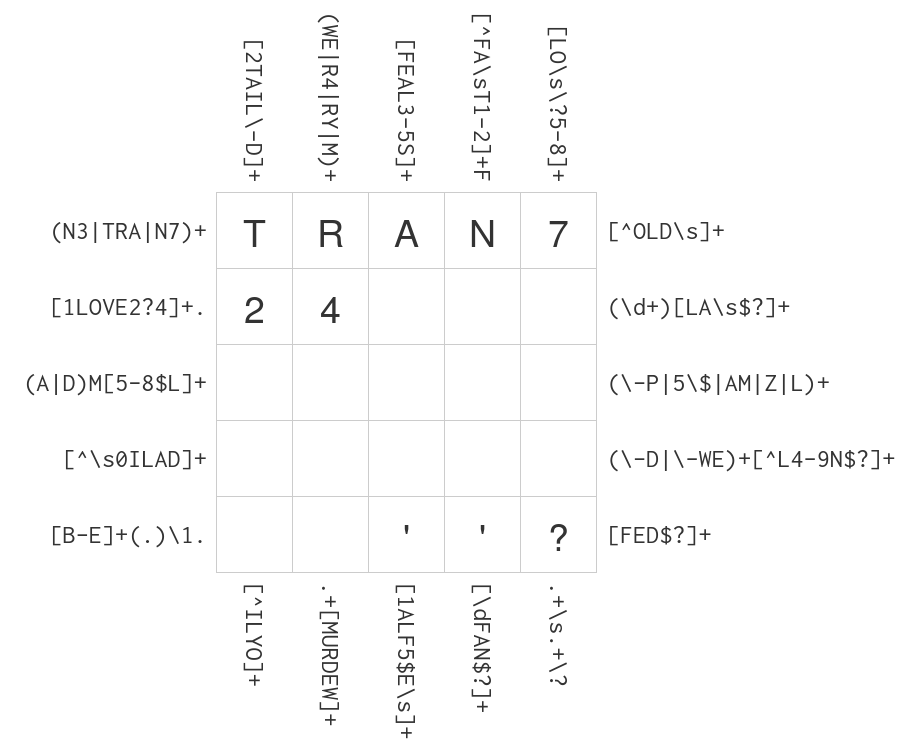
# As you can see, an instance of this game is determined by its rectangular size, let's denote it $(m, n)$, so here there are $m=5$ lines and $n=5$ columns.
#
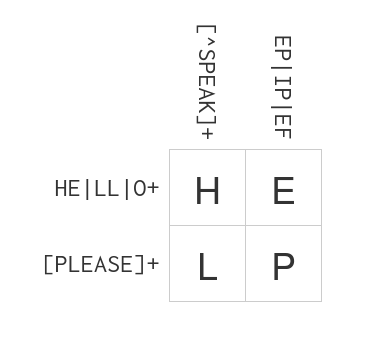
# I'll also use this [easy problem](https://regexcrossword.com/challenges/beginner/puzzles/1):
#
# 
#
# Let's define both, in a small dictionnary containing two to four lists of regexps.
# ### Easy problem of size $(2,2)$ with four constraints
# In[1]:
problem1 = {
"left_lines": [
r"HE|LL|O+", # HE|LL|O+ line 1
r"[PLEASE]+", # [PLEASE]+ line 2
],
"right_lines": None,
"top_columns": [
r"[^SPEAK]+", # [^SPEAK]+ column 1
r"EP|IP|EF", # EP|IP|EF column 2
],
"bottom_columns": None,
}
# The keys `"right_lines"` and `"bottom_columns"` can be empty, as for easier problems there are no constraints on the right and bottom.
# Each line and column (but not each square) contains a regular expression, on a common alphabet of letters and symbols.
# Let's write $\Sigma$ this alphabet, which in the most general case is $\Sigma=\{$ `A`, `B`, ..., `Z`, `0`, ..., `9`, `:`, `?`, `.`, `$`, `-`$\}$.
# For the first beginner problem, the alphabet can be shorten:
# In[2]:
alphabet1 = {
'H', 'E', 'L', 'O',
'P', 'L', 'E', 'A', 'S', 'E',
'S', 'P', 'E', 'A', 'K',
'E', 'P', 'I', 'P', 'I', 'F',
}
print(f"alphabet1 = \n{sorted(alphabet1)}")
# ### Difficult problem of size $(5,5)$ with 20 constraints
# Defining the [second problem](https://regexcrossword.com/challenges/volapuk/puzzles/5) is just a question of more copy-pasting:
# In[3]:
problem2 = {
"left_lines": [
r"(N3|TRA|N7)+", # left line 1
r"[1LOVE2?4]+.", # left line 2
r"(A|D)M[5-8$L]+", # left line 3
r"[^\s0ILAD]+", # left line 4
r"[B-E]+(.)\1.", # left line 5
],
"right_lines": [
r"[^OLD\s]+", # right line 1
r"(\d+)[LA\s$?]+", # right line 2
r"(\-P|5\$|AM|Z|L)+", # right line 3
r"(\-D|\-WE)+[^L4-9N$?]+", # right line 4
r"[FED$?]+", # right line 5
],
"top_columns": [
r"[2TAIL\-D]+", # top column 1
r"(WE|R4|RY|M)+", # top column 2
r"[FEAL3-5S]+", # top column 3
r"[^FA\sT1-2]+F", # top column 4
r"[LO\s\?5-8]+", # top column 5
],
"bottom_columns": [
r"[^ILYO]+", # top column 1
r".+[MURDEW]+", # top column 2
r"[1ALF5$E\s]+", # top column 3
r"[\dFAN$?]+", # top column 4
r".+\s.+\?", # top column 5
],
}
# And its alphabet:
# In[4]:
import string
# In[5]:
alphabet2 = set(string.digits) | set(string.ascii_uppercase) | { ':', '?', '.', '$', '-', ' ' }
print(f"alphabet2 = \n{sorted(alphabet2)}")
# ### An intermediate problem of size $(3,3)$ with 12 constraints
# Defining the [third problem](https://regexcrossword.com/challenges/doublecross/puzzles/3) is just a question of more copy-pasting:
# In[6]:
problem3 = {
"left_lines": [
r"[ONE]*[SKA]", # left line 1
r".*(RE|ER)", # left line 2
r"A+[TUB]*", # left line 3
],
"right_lines": [
r".*(O|S)*", # right line 1
r"[^GOA]*", # right line 2
r"[STUPA]+", # right line 3
],
"top_columns": [
r".*[GAF]*", # top column 1
r"(P|ET|O|TEA)*", # top column 2
r"[RUSH]+", # top column 3
],
"bottom_columns": [
r"(NF|FA|A|FN)+", # top column 1
r".*(A|E|I).*", # top column 2
r"[SUPER]*", # top column 3
],
}
# And its alphabet:
# In[7]:
alphabet3 = {
'O', 'N', 'E', 'S', 'K', 'A',
'R', 'E', 'E', 'R',
'A', 'T', 'U', 'B',
'O', 'S',
'G', 'O', 'A',
'S', 'T', 'U', 'P', 'A',
'G', 'A', 'F',
'P', 'E', 'T', 'O', 'T', 'E', 'A',
'R', 'U', 'S', 'H',
'N', 'F', 'F', 'A', 'A', 'F', 'N',
'A', 'E', 'I',
'S', 'U', 'P', 'E', 'R',
}
print(f"alphabet3 = \n{sorted(alphabet3)}")
# ### A few useful functions
#
# Let's first extract the dimension of a problem:
# In[8]:
from typing import Tuple, Dict, List, Set, Any, Union
def dimension_problem(problem: dict) -> Tuple[int, int]:
m = len(problem['left_lines'])
if problem['right_lines'] is not None:
assert m == len(problem['right_lines'])
n = len(problem['top_columns'])
if problem['bottom_columns'] is not None:
assert n == len(problem['bottom_columns'])
return (m, n)
# In[9]:
problem1
# In[10]:
dimension_problem(problem1)
# Now let's write a representation of a grid, a solution (or partial solution) of a problem:
# In[11]:
___ = "_" # represents an empty answer, as _ is not in the alphabet
grid1_partial = [
[ 'H', ___ ],
[ ___, 'P' ],
]
# In[12]:
grid1_solution = [
[ 'H', 'E' ],
[ 'L', 'P' ],
]
# As well as a few complete grids which are NOT solutions
# In[13]:
grid1_wrong1 = [
[ 'H', 'E' ],
[ 'L', 'F' ],
]
# In[14]:
grid1_wrong2 = [
[ 'H', 'E' ],
[ 'E', 'P' ],
]
# In[15]:
grid1_wrong3 = [
[ 'H', 'E' ],
[ 'O', 'F' ],
]
# In[16]:
grid1_wrong4 = [
[ 'O', 'E' ],
[ 'O', 'F' ],
]
# We also write these short functions to extract the $i$-th line or $j$-th column:
# In[17]:
def nth_line(grid: List[List[str]], line: int) -> str:
return "".join(grid[line])
def nth_column(grid: List[List[str]], column: int) -> str:
return "".join(grid[line][column] for line in range(len(grid)))
# In[18]:
[ nth_line(grid1_solution, line) for line in range(len(grid1_solution)) ]
# In[19]:
[ nth_column(grid1_solution, column) for column in range(len(grid1_solution[0])) ]
# A partial solution for the intermediate problem:
# In[20]:
___ = "_" # represents an empty answer, as _ is not in the alphabet
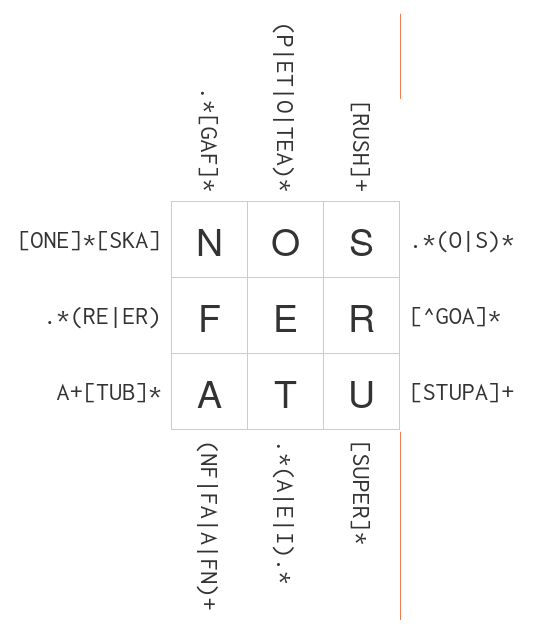
grid3_solution = [
[ 'N', 'O', 'S' ],
[ 'F', 'E', 'R' ],
[ 'A', 'T', 'U' ],
]
# And a partial solution for the harder problem:
# In[21]:
___ = "_" # represents an empty answer, as _ is not in the alphabet
grid2_partial = [
[ 'T', 'R', 'A', 'N', '7' ],
[ '2', '4', ___, ___, ' ' ],
[ 'A', ___, ___, ___, ___ ],
[ '-', ___, ___, ___, ___ ],
[ 'D', ___, ___, ___, '?' ],
]
# Let's extract the dimension of a grid, just to check it:
# In[22]:
def dimension_grid(grid: List[List[str]]) -> Tuple[int, int]:
m = len(grid)
n = len(grid[0])
assert all(n == len(grid[i]) for i in range(1, m))
return (m, n)
# In[23]:
print(f"Grid grid1_partial has dimension: {dimension_grid(grid1_partial)}")
print(f"Grid grid1_solution has dimension: {dimension_grid(grid1_solution)}")
# In[24]:
print(f"Grid grid2_partial has dimension: {dimension_grid(grid2_partial)}")
# In[25]:
def check_dimensions(problem: dict, grid: List[List[int]]) -> bool:
return dimension_problem(problem) == dimension_grid(grid)
# In[26]:
assert check_dimensions(problem1, grid1_partial)
assert check_dimensions(problem1, grid1_solution)
# In[27]:
assert not check_dimensions(problem2, grid1_partial)
# In[28]:
assert check_dimensions(problem2, grid2_partial)
# In[29]:
assert not check_dimensions(problem1, grid2_partial)
# ### Two more checks
#
# We also have to check if a word is in an alphabet:
# In[30]:
def check_alphabet(alphabet: Set[str], word: str, debug: bool=True) -> bool:
result = True
for i, letter in enumerate(word):
new_result = letter in alphabet
if debug and result and not new_result:
print(f"The word {repr(word)} is not in alphabet {repr(alphabet)}, as its #{i}th letter {letter} is not present.")
result = result and new_result
return result
# In[31]:
assert check_alphabet(alphabet1, 'H' 'E') # concatenate the strings
# In[32]:
assert check_alphabet(alphabet1, 'H' 'E')
assert check_alphabet(alphabet1, 'L' 'P')
assert check_alphabet(alphabet1, 'H' 'L')
assert check_alphabet(alphabet1, 'E' 'P')
# In[33]:
assert check_alphabet(alphabet2, "TRAN7")
# And also check that a word matches a regexp:
# In[34]:
import re
# As the [documentation](https://docs.python.org/3/library/re.html#re.compile) explains it:
#
# > but using `prog = re.compile(regepx)` and saving the resulting regular expression object `prog` for reuse is more efficient when the expression will be used several times in a single program.
#
# I don't want to have to think about compiling a regexp before using it, so... I'm gonna memoize them!
# In[42]:
memory_of_compiled_regexps = dict()
# Now we are ready to write our "smart" match function:
# In[43]:
def match(regexp: str, word: str, debug: bool=True) -> bool:
global memory_of_compiled_regexps
if regexp not in memory_of_compiled_regexps:
prog = re.compile(regexp)
memory_of_compiled_regexps[regexp] = prog
print(f"For the first time seeing this regexp {repr(regexp)}, compiling it and storing in memory_of_compiled_regexps, now of size {len(memory_of_compiled_regexps)}.")
else:
prog = memory_of_compiled_regexps[regexp]
# XXX This is slow!
# result = re.fullmatch(regexp, word)
# DONE This is faster!
result = prog.fullmatch(word)
entire_match = result is not None
if debug:
if entire_match:
print(f"The word {repr(word)} is matched by {repr(regexp)}")
else:
print(f"The word {repr(word)} is NOT matched by {repr(regexp)}")
return entire_match
# Let's compare the time of the first match and next ones:
# In[44]:
match(r"(N3|TRA|N7)+", "TRAN7")
# In[45]:
match(r"(N3|TRA|N7)+", "TRAN8")
# Well of course it's not different for tiny test like this.
# In[ ]:
match(r"(N3|TRA|N7)+", "")
# In[ ]:
match(r"(N3|TRA|N7)+", "TRA")
# That should be enough to start the first "easy" task.
# In[47]:
match(r"(N3|TRA|N7)+", "TRA", debug=False)
re.fullmatch(r"(N3|TRA|N7)+", "TRA")
# We can see that our "memoization trick" indeed helped to speed-up the time required to check a regexp, by about a factor 2, even for very small tests like this.
# ## First easy task: check that a line/column word validate its contraints
#
# Given a problem $P$ of dimension $(m, n)$, its alphabet $\Sigma$, a position $i \in [| 0, m-1 |]$ of a line or $j \times [|0, n-1 |]$ of a column, and a word $w \in \Sigma^k$ (with $k=m$ for line or $k=n$ for column), I want to write a function that checks the validity of each (left/right) line, or (top/bottom) constraints.
#
# To ease debugging, and in the goal of using this Python program to improve my skills in solving such puzzles, I don't want this function to just reply `True` or `False`, but to also print for each constraints if it is satisfied or not.
#
# **Bonus:** for each regexp contraint, highlight the parts which corresponded to each letter of the word?
# ### For lines
# We are ready to check the one or two constraints of a line.
# The same function will be written for columns, just below.
# In[48]:
def check_line(problem: dict, alphabet: Set[str], word: str, position: int, debug: bool=True, early: bool=False) -> bool:
if not check_alphabet(alphabet, word, debug=debug):
return False
m, n = dimension_problem(problem)
if len(word) != n:
if debug:
print(f"Word {repr(word)} does not have correct size n = {n} for lines")
return False
assert 0 <= position < m
constraints = []
if "left_lines" in problem and problem["left_lines"] is not None:
constraints += [ problem["left_lines"][position] ]
if "right_lines" in problem and problem["right_lines"] is not None:
constraints += [ problem["right_lines"][position] ]
# okay we have one or two constraint for this line,
assert len(constraints) in {1, 2}
# let's check them!
result = True
for cnb, constraint in enumerate(constraints):
if debug:
print(f"For line constraint #{cnb} {repr(constraint)}:")
new_result = match(constraint, word, debug=debug)
if early and not new_result: return False
result = result and new_result
return result
# Let's try it!
# In[49]:
print(problem1, alphabet1, grid1_solution)
# In[50]:
n, m = dimension_problem(problem1)
for line in range(n):
word = nth_line(grid1_solution, line)
print(f"- For line number {line}, checking word {repr(word)}:")
result = check_line(problem1, alphabet1, word, line)
# In[51]:
n, m = dimension_problem(problem1)
fake_words = ["OK", "HEY", "NOT", "HELL", "N", "", "HU", "OO", "EA"]
for word in fake_words:
print(f"# For word {repr(word)}:")
for line in range(n):
result = check_line(problem1, alphabet1, word, line)
print(f" => {result}")
# That was long, but it works fine!
# In[52]:
n, m = dimension_problem(problem2)
for line in [0]:
word = nth_line(grid2_partial, line)
print(f"- For line number {line}, checking word {repr(word)}:")
result = check_line(problem2, alphabet2, word, line)
print(f" => {result}")
# In[53]:
n, m = dimension_problem(problem2)
fake_words = [
"TRAN8", "N2TRA", # violate first constraint
"N3N3N7", "N3N3", "TRA9", # smaller or bigger dimension
"O L D", "TRA ", # violate second contraint
]
for word in fake_words:
for line in [0]:
print(f"- For line number {line}, checking word {repr(word)}:")
result = check_line(problem2, alphabet2, word, line)
print(f" => {result}")
# ### For columns
# We are ready to check the one or two constraints of a line.
# The same function will be written for columns, just below.
# In[54]:
def check_column(problem: dict, alphabet: Set[str], word: str, position: int, debug: bool=True, early: bool=False) -> bool:
if not check_alphabet(alphabet, word, debug=debug):
return False
m, n = dimension_problem(problem)
if len(word) != m:
if debug:
print(f"Word {repr(word)} does not have correct size n = {n} for columns")
return False
assert 0 <= position < n
constraints = []
if "top_columns" in problem and problem["top_columns"] is not None:
constraints += [ problem["top_columns"][position] ]
if "bottom_columns" in problem and problem["bottom_columns"] is not None:
constraints += [ problem["bottom_columns"][position] ]
# okay we have one or two constraint for this column,
assert len(constraints) in {1, 2}
# let's check them!
result = True
for cnb, constraint in enumerate(constraints):
if debug:
print(f"For column constraint #{cnb} {repr(constraint)}:")
new_result = match(constraint, word, debug=debug)
if early and not new_result: return False
result = result and new_result
return result
# Let's try it!
# In[55]:
print(problem1, alphabet1, grid1_solution)
# In[56]:
n, m = dimension_problem(problem1)
for column in range(m):
word = nth_column(grid1_solution, column)
print(f"- For column number {column}, checking word {repr(word)}:")
result = check_column(problem1, alphabet1, word, column)
print(result)
# In[57]:
n, m = dimension_problem(problem1)
fake_words = ["OK", "HEY", "NOT", "HELL", "N", "", "HU", "OO", "EA"]
for word in fake_words:
print(f"# For word {repr(word)}:")
for column in range(m):
result = check_column(problem1, alphabet1, word, column)
print(f" => {result}")
# That was long, but it works fine!
# In[58]:
n, m = dimension_problem(problem2)
for column in [0]:
word = nth_column(grid2_partial, column)
print(f"- For column number {column}, checking word {repr(word)}:")
result = check_column(problem2, alphabet2, word, column)
print(f" => {result}")
# In[59]:
n, m = dimension_problem(problem2)
fake_words = [
"TRAN8", "N2TRA", # violate first constraint
"N3N3N7", "N3N3", "TRA9", # smaller or bigger dimension
"O L D", "TRA ", # violate second contraint
]
for word in fake_words:
for line in [0]:
print(f"- For line number {line}, checking word {repr(word)}:")
result = check_column(problem2, alphabet2, word, line)
print(f" => {result}")
# ## Second easy task: check that a proposed grid is a valid solution
#
# I think it's easy, as we just have to use $m$ times the `check_line` and $n$ times the `check_column` functions.
# In[60]:
def check_grid(problem: dict, alphabet: Set[str], grid: List[List[str]], debug: bool=True, early: bool=False) -> bool:
m, n = dimension_problem(problem)
ok_lines = [False] * m
for line in range(m):
word = nth_line(grid, line)
ok_lines[line] = check_line(problem, alphabet, word, line, debug=debug, early=early)
ok_columns = [False] * n
for column in range(n):
word = nth_column(grid, column)
ok_columns[column] = check_column(problem, alphabet, word, column, debug=debug, early=early)
# TODO: of course we could be more efficient than computing all the bool and taking all(...), by doing early stopping
# Worst case stays O(n + m) so I don't care
return all(ok_lines) and all(ok_columns)
# Let's try it!
# ### For the easy problem
# For a partial grid, of course it's going to be invalid just because `'_'` is *not* in the alphabet $\Sigma$.
# In[61]:
check_grid(problem1, alphabet1, grid1_partial)
# For a complete grid, let's check that our solution is valid:
# In[62]:
check_grid(problem1, alphabet1, grid1_solution)
# And let's also check that the few wrong solutions are indeed not valid:
# In[63]:
check_grid(problem1, alphabet1, grid1_wrong1)
# In[64]:
check_grid(problem1, alphabet1, grid1_wrong2)
# In[65]:
check_grid(problem1, alphabet1, grid1_wrong3)
# In[66]:
check_grid(problem1, alphabet1, grid1_wrong4)
# We can see that for each wrong grid, at least one of the contraint is violated!
#
# That's pretty good!
# ### For the intermediate problem
#
# My solution for the intermediate problem `problem3` is indeed valid:
#
# 
# In[67]:
check_grid(problem3, alphabet3, grid3_solution)
# ### For the hard problem
#
# Well I don't have a solution yet, so I cannot check it!
# ## Third easy task: generate all words of a given size in the alphabet
#
# Using [`itertools.product`](https://docs.python.org/3/library/itertools.html#itertools.product) and the alphabet defined above, it's going to be easy.
#
# Note that I'll first try with a smaller alphabet, to check the result (for problem 1).
# In[68]:
import itertools
# In[69]:
from typing import Generator
def all_words_of_alphabet(alphabet: Union[List[str], Set[str]], size: int) -> Generator:
yield from itertools.product(alphabet, repeat=size)
# Just a quick check:
# In[70]:
list(all_words_of_alphabet(['0', '1'], 3))
# The time and memory complexity of this function should be $\mathcal{O}(|\Sigma|^k)$ for words of size $k\in\mathbb{N}^*$.
# In[71]:
alphabet0 = ['0', '1']
len_alphabet = len(alphabet0)
for k in [2, 3, 4, 5]:
print(f"Generating {len_alphabet**k} words of size = {k} takes about")
list(all_words_of_alphabet(alphabet0, k))
# In[72]:
list(all_words_of_alphabet(['0', '1', '2', '3'], 10))
# We can quickly check that even for the larger alphabet of size ~40, it's quite quick for small words of length $\leq 5$:
# In[73]:
len_alphabet = len(alphabet1)
for k in [2, 3, 4, 5]:
print(f"Generating {len_alphabet**k} words of size = {k} takes about")
list(all_words_of_alphabet(alphabet1, k))
# In[74]:
# len_alphabet = len(alphabet2)
# for k in [2, 3, 4, 5]:
# print(f"Generating {len_alphabet**k} words of size = {k} takes about")
# list(all_words_of_alphabet(alphabet2, k))
# Who, it takes 12 seconds to just *generate* all the possible words for the largest problem (which is just of size $(5,5)$)...
#
# I'm afraid that my naive approach to solve the puzzle will be VERY slow...
# ## Fourth easy task: generate all grids of a given size
# In[75]:
def all_grids_of_alphabet(alphabet: Union[List[str], Set[str]], lines: int, columns: int) -> Generator:
all_words = list(itertools.product(alphabet, repeat=columns))
all_words = [ "".join(words) for words in all_words ]
all_grids = itertools.product(all_words, repeat=lines)
for pre_tr_grid in all_grids:
tr_grid = [
[
pre_tr_grid[line][column]
for line in range(lines)
]
for column in range(columns)
]
yield tr_grid
# In[76]:
for alphabet in ( ['0', '1'], ['T', 'A', 'C', 'G'] ):
for (n, m) in [ (1, 1), (2, 2), (1, 2), (2, 1), (3, 3), (3, 2), (2, 3) ]:
assert len(list(all_grids_of_alphabet(alphabet, n, m))) == len(alphabet)**(n*m)
print(list(all_grids_of_alphabet(alphabet0, n, m))[0])
print(list(all_grids_of_alphabet(alphabet0, n, m))[-1])
# In[77]:
print(f"For the alphabet {alphabet0} of size = {len(alphabet0)} :")
for (n, m) in [ (1, 1), (2, 1), (1, 2), (2, 2) ]:
all_these_grids = list(all_grids_of_alphabet(alphabet0, n, m))
print(f"For (n, m) = {(n, m)} the number of grids is {len(all_these_grids)}")
# ### How long does it take and how many grids for the easy problem?
# In[78]:
print(f"For the alphabet {alphabet1} of size = {len(alphabet1)} :")
for (n, m) in [ (1, 1), (2, 1), (1, 2), (2, 2) ]:
all_these_grids = list(all_grids_of_alphabet(alphabet1, n, m))
print(f"For (n, m) = {(n, m)} the number of grids is {len(all_these_grids)}")
# That's still pretty small and fast!
# ### How long does it take and how many grids for the hard problem?
# In[79]:
print(f"For the alphabet {alphabet2} of size = {len(alphabet2)} :")
for (n, m) in [ (1, 1), (2, 1), (1, 2), (2, 2) ]:
all_these_grids = list(all_grids_of_alphabet(alphabet2, n, m))
print(f"For (n, m) = {(n, m)} the number of grids is {len(all_these_grids)}")
# In[80]:
41**(2*3)
# Just for $(n, m) = (2, 2)$ it takes about 7 seconds...
# So to scale for $(n, m) = (5, 5)$ would just take... WAY TOO MUCH TIME!
# In[81]:
n, m = 5, 5
41**(5*5)
# In[82]:
import math
# In[83]:
math.log10(41**(5*5))
# For a grid of size $(5,5)$, the number of different possible grids is about $10^{40}$, that is CRAZY large, we have no hope of solving this problem with a brute force approach.
#
# How much time would that require, just to generate the grids?
# In[84]:
s = 7
estimate_of_running_time = 7*s * len(alphabet1)**(5*5) / len(alphabet1)**(2*2)
estimate_of_running_time # in seconds
# This rough estimate gives about $5 * 10^{22}$ seconds, about $10^{15}$ years, so about a million of billion years !
# In[85]:
math.log10( estimate_of_running_time / (60*60*24*365) )
# ## First difficult task: for each possible grid, check if its valid
# In[91]:
def naive_solve(problem: dict, alphabet: Union[List[str], Set[str]], debug: bool=False, early: bool=True) -> List[List[List[str]]]:
n, m = dimension_problem(problem)
good_grids = []
for possible_grid in all_grids_of_alphabet(alphabet, n, m):
is_good_grid = check_grid(problem, alphabet, possible_grid, debug=debug, early=early)
if is_good_grid:
if early:
return [ possible_grid ]
good_grids.append(possible_grid)
return good_grids
# Let's try it!
# ### Solving the easy problem
# Let's check that we can quickly find *one* solution:
# In[92]:
good_grids1 = naive_solve(problem1, alphabet1, debug=False, early=True)
print(f"For problem 1\\n{problem1}\\nOn alphabet\{alphabet1}\\n==> We found one solution:\\n{good_grids1}")
# Then can we find more solutions?
# In[93]:
good_grids1 = naive_solve(problem1, alphabet1, debug=False, early=False)
print(f"For problem 1\\n{problem1}\\nOn alphabet\{alphabet1}\\n==> We found these solutions:\\n{good_grids1}")
# No there is indeed a unique solution here for the first "easy" problem!
# ### Solving the intermediate problem
# In[261]:
# good_grids3 = naive_solve(problem3, alphabet3, debug=False, early=True)
# print(f"For problem 3\\n{problem3}\\nOn alphabet\{alphabet3}\\n==> We found one solution:\\n{good_grids3}")
# That was so long...
#
# I could try to use Pypy3 IPython kernel, to speed things up?
#
# > Yes it's possible to use a Pypy kernel from your regular Python notebook!
# > See
# ### Solving the hard problem
#
# Most probably, it will run forever if I use the naive approach of:
#
# - generate all grids of $m$ words of size $n$ in given alphabet $\Sigma$ ;
# - for all grid:
# + test it using naive algorithm
# + if it's valid: adds it to the list of good grids
#
# There are $|\Sigma|^{n \times m}$ possible grids, so this approach is doubly exponential in $n$ for square grids.
#
# I must think of a better approach...
# Being just exponential in $\max(m, n)$ would imply that it's practical for the harder problem of size $(5,5)$.
# In[192]:
# good_grids2 = naive_solve(problem2, alphabet2, debug=False, early=True)
# print(f"For problem 2\\n{problem2}\\nOn alphabet\{alphabet2}\\n==> We found one solution:\\n{good_grids2}")
# My first idea was to try to tackle each constraint independently, and generate the set of words that satisfy this contraint. (by naively checking `check(constraint, word)` for each word in $\Sigma^n$ or $\Sigma^m$).
#
# - if there are two line constraints (left/right), get the intersection of the two sets of words;
# - then, *for each* line we have a set of possible words:
# + we can build each column, and then check that the top/bottom constraint is valid or not
# + if valid, continue to next column until the last
# + if all columns are valid, then these lines/columns form a possible grid!
# + (if we want only one solution, stop now, otherwise continue)
# ## Second difficult task: a more efficient approach to solve any problem
# In[94]:
n, m = dimension_problem(problem1)
# In[95]:
problem1
# In[96]:
alphabet1
# In[97]:
len(list(all_words_of_alphabet(alphabet1, n)))
# In[98]:
["".join(word) for word in list(all_words_of_alphabet(alphabet1, n))][:10]
# In[99]:
[
[ "".join(word)
for word in all_words_of_alphabet(alphabet1, n)
if check_line(problem1, alphabet1, "".join(word), line, debug=False, early=True)
]
for line in range(m)
]
# In[100]:
[
[ "".join(word)
for word in all_words_of_alphabet(alphabet1, m)
if check_column(problem1, alphabet1, "".join(word), column, debug=False, early=True)
]
for column in range(n)
]
# So let's write this algorithm.
#
# I'm using a [`tqdm.tqdm()`](https://tqdm.github.io/docs/notebook/) wrapper on the foor loops, to keep an eye on the progress.
# In[101]:
# from tqdm.notebook import trange, tqdm
from tqdm import trange, tqdm
# In[102]:
def smart_solve(problem: dict, alphabet: Union[List[str], Set[str]], debug: bool=True, early: bool=True) -> List[List[List[str]]]:
n, m = dimension_problem(problem)
good_grids = []
possible_words_for_lines = [
[ "".join(word)
for word in all_words_of_alphabet(alphabet, n)
if check_line(problem, alphabet, "".join(word), line, debug=False, early=True)
# TODO don't compute this "".join(word) twice?
]
for line in range(m)
]
number_of_combinations = 1
for line in range(m):
number_of_combinations *= len(possible_words_for_lines[line])
print(f"- There are {len(possible_words_for_lines[line])} different words for line #{line}")
print(f"=> There are {number_of_combinations} combinations of words for lines #{0}..#{m-1}\n\n")
nb_combination = 0
for possible_words in itertools.product(*possible_words_for_lines):
nb_combination += 1
percentage = 100 * nb_combination / float(number_of_combinations)
if debug: print(f"{percentage:.3g}% Trying possible_words #{nb_combination}/{number_of_combinations}, from line constraints = {possible_words}")
column = 0
no_wrong_column = True
while no_wrong_column and column < n:
word_column = "".join(possible_words[line][column] for line in range(m))
if debug: print(f" For column #{column}, word = {word_column}, checking constraint...")
if not check_column(problem, alphabet, word_column, column, debug=False, early=True):
# this word is NOT valid for this column, so let's go to the next word
if debug: print(f" This word {word_column} is NOT valid for this column {column}, so let's go to the next word")
no_wrong_column = False
# break: this was failing... broke the outer for-loop and not the inner one
column += 1
if no_wrong_column:
print(f" These words seemed to satisfy the column constraints!\n{possible_words}")
# so all columns are valid! this choice of words is good!
possible_grid = [
list(word) for word in possible_words
]
print(f"Giving this grid:\n{possible_grid}")
# let's check it, just in case (this takes a short time, compared to the rest)
is_good_grid = check_grid(problem, alphabet, possible_grid, debug=debug, early=early)
if is_good_grid:
if early:
return [ possible_grid ]
good_grids.append(possible_grid)
# after the outer for loop on possible_words
return good_grids
# And let's try it:
# ### For the easy problem
# In[103]:
print(grid1_solution)
# In[104]:
good_grids1 = smart_solve(problem1, alphabet1)
print("Solution good_grids1 =", good_grids1)
# So it worked!
#
# 🚀 It was also *BLAZING* fast compared to the naive approach: 160ms against about 900µs, almost a 160x speed-up factor!
#
# 🤔 *I don't understand why it's so slow now* I did get a time of 900 µs at first try, now it's about 90 ms... just a 2x spee-up factor.
#
# Let's try for the harder problem!
# ### For the intermediate problem
# In[106]:
import time
before = time.time()
print(f"\n\n\n\nFiding solution for problem3 = {problem3} on alphabet = {alphabet3}...")
good_grids3 = smart_solve(problem3, alphabet3)
print(f"Solution good_grids3 = {good_grids3}")
after = time.time()
delta_time = after - before
print(f"Found this solution for problem3 in about {delta_time} seconds.")
# 🚀 It was also *BLAZING* fast compared to the naive approach: 90ms, when the naive approach was just too long that I killed it...
# ### For the harder problem
# In[ ]:
before = time.time()
print(f"\n\n\n\nFiding solution for problem2 = {problem2} on alphabet = {alphabet2}...")
good_grids2 = smart_solve(problem2, alphabet2)
print(f"Solution good_grids2 = {good_grids2}")
after = time.time()
delta_time = after - before
print(f"Found this solution for problem2 in about {delta_time} seconds.")
# It made my kernel restart...
# ## Improve the solution - TODO
#
# > If you're extra curious about this puzzle problem, and my experiments, you can continue from here and finish these ideas:
#
# - It could be great if it were be possible to give a partially filled grid, and start from there.
#
# - It could also be great to just be able to fill *one* cell in the grid, in case you're blocked and want some hint.
# ## My feeling about these problems and my solutions
#
# I could have tried to be more efficient, but I didn't have much time to spend on this.
# ## Conclusion
#
# That was nice! Writing this notebook took about 4.5 hours entirely, from first idea to final edit, on Sunday 28th of February, 2021. (note that I was also cooking my [pancakes](https://perso.crans.org/besson/cuisine/pancakes.html) during the first half, so I wasn't intensely coding)
#
# Have a look at [my other notebooks](https://GitHub.com/Naereen/notebooks/).