(* # Texte d'oral de modélisation - Agrégation Option Informatique *)
(* ## Préparation à l'agrégation - ENS de Rennes, 2016-17 *)
(* - *Date* : 3 avril 2017 *)
(* - *Auteur* : [Lilian Besson](https://GitHub.com/Naereen/notebooks/) *)
(* - *Texte*: Annale 2006, "Sudoku" *)
(* ## À propos de ce document *)
(* - Ceci est une *proposition* de correction, partielle et probablement non-optimale, pour la partie implémentation d'un [texte d'annale de l'agrégation de mathématiques, option informatique](http://Agreg.org/Textes/). *)
(* - Ce document est un [notebook Jupyter](https://www.Jupyter.org/), et [est open-source sous Licence MIT sur GitHub](https://github.com/Naereen/notebooks/tree/master/agreg/), comme les autres solutions de textes de modélisation que [j](https://GitHub.com/Naereen)'ai écrite cette année. *)
(* - L'implémentation sera faite en OCaml, version 4+ : *)
(* In[1]: *)
Sys.command "ocaml -version";;
(* ---- *)
(* ## Question de programmation *)
(* La question de programmation pour ce texte était donnée au tout début, en page 2 : *)
(* > « Écrire une fonction prenant pour paramètres un entier, $p \geq 1$, et un tableau carré de côté $p$ (donc de taille $p^2$) d'entiers, $T$, et renvoyant un booléen disant si ce tableau est un carré latin, c'est-à-dire contenant dans chaque ligne et chaque colonne une et une seule fois chaque entier de $1$ à $p$. *)
(* Mathématiquement, si $N_p := \{1,\dots,p\}$, cela donne un prédicat $\mathrm{estCarreLatin}_p(T)$ sur un tableau $T$ : *)
(* $$ *)
(* \mathrm{estCarreLatin}_p(T) \Longleftrightarrow *)
(* \forall i \in N_p, \left\{ T_{i,j} : j \in N_p \right\} = N_p *)
(* \;\text{and}\; *)
(* \forall j \in N_p, \left\{ T_{i,j} : i \in N_p \right\} = N_p *)
(* $$ *)
(* > « En prenant $p = n^2$ on obtient une partie des contraintes d'admissibilité d'une grille complète de Su Doku, mais il reste encore à vérifier la contrainte sur les petits carrés. » *)
(* Pour l'annecdote historique, cette idée de carré latin date vraiment de l'époque romaine antique. On a trouvé à Pompeï des carrés latins de taille $4$ ou $5$ ! *)
(* ---- *)
(* ## Réponse à l'exercice requis *)
(* C'est assez rapide : *)
(* 1. On écrit une fonction qui permet d'extraire une ligne ou une colonne d'un tableau $T$, *)
(* 2. On écrit ensuite une fonction qui permet de vérifier si un tableau de $p$ entiers contient exactement $N_p = \{1, \dots, p\}$, *)
(* 3. Enfin, on vérifie toutes les contraintes. *)
(* > *Remarque:* On suppose que tous les tableaux considérés sont : *)
(* > - **non vides** *)
(* > - et **carrés** *)
(* > On ne vérifie pas ces deux points. *)
(* In[2]: *)
let ligne p t i = Array.init p (fun j -> t.(i).(j)) ;;
(* t.(i) marche aussi bien ! *)
let colonne p t j = Array.init p (fun i -> t.(i).(j)) ;;
(* On a besoin de savoir si un tableau de booléens sont tous vrais ou pas. *)
(* On peut utiliser la fonction déjà existante, `Array.for_all`, ou bien un `Array.fold_left`, ou une implémentation manuelle. *)
(* In[3]: *)
let tousVrai tab =
let res = ref true in
for i = 0 to (Array.length tab) - 1 do
res := !res && tab.(i)
done;
!res
;;
(* In[4]: *)
let tousVrai = Array.fold_left (&&) true;;
(* Array.for_all marche aussi bien ! *)
(* Ca permet de facilement vérifier si un tableau `tab` de taille $p$ est exactement $N_p = \{1,\dots,p\}$, en temps linéaire (c'est optimal) en $p$. *)
(* 1. On ajoute un test que tous les entiers soient bien entre $1$ et $p$, *)
(* 2. puis on fait ce test en $\mathcal{O}(\# tab)$, en créant est un tableau `estLa` de taille $p$, remplis de `false`. En bouclant sur $t$, on remplit $\texttt{tab}[i]$ à `true` dans `estLa` (en fait, `tab(i) - 1` car les indices sont entre $0$ et $p-1$). A la fin, si le tableau `estLa` est rempli de `true`, alors on a vu tous les entiers de $N_p$ une et une seule fois. *)
(* In[5]: *)
let estNp p tab =
if tousVrai (Array.map (fun x -> (1 <= x) && (x <= p)) tab) then begin
let estLa = Array.make p false in
for i = 0 to p - 1 do
estLa.(tab.(i) - 1) <- true
done;
tousVrai estLa
end
else
false
;;
(* On va adopter une méthode naïve mais simple à écrire : *)
(* - on construit deux tableaux de $p$ booléens, *)
(* - on les remplit des contraintes pour les $p$ lignes et les $p$ colonnes, *)
(* - et on les vérifie avec `tousVrai`. *)
(* In[32]: *)
let contraintes_lignes p t =
tousVrai (Array.init p (fun i ->
estNp p (ligne p t i)
))
;;
(* In[31]: *)
let contraintes_colonnes p t =
tousVrai (Array.init p (fun j ->
estNp p (colonne p t j)
))
;;
(* In[7]: *)
let carre_latin p t =
(contraintes_lignes p t) && (contraintes_colonnes p t)
;;
(* ### Une autre approche *)
(* Plutôt que d'écrire une fonction pour extraire une colonne, et deux fonction qui vérifies les contraintes sur les lignes et les colonnes, on remarque le fait suivant : *)
(* > « Les colonnes de $t$ sont les lignes de $t^T$, la matrice transposée de $t$ ». *)
(* Donc pas besoin de savoir extraire les colonnes, dès qu'on a écrit `contraintes_lignes`, on peut avoir les contraintes sur les colonnes facilement. *)
(* Pour calculer la transposée, une approche simple utilise deux boucles `for` : *)
(* In[8]: *)
let transpose_for p tab =
let tab2 = Array.make_matrix p p 0 in
for i = 0 to p - 1 do
for j = 0 to p - 1 do
tab2.(i).(j) <- tab.(j).(i);
done;
done;
tab2
;;
(* On peut rapidement vérifier sur un exemple, *)
(* $$ \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}^{T} = \begin{bmatrix} 1 & 3 \\ 2 & 4 \end{bmatrix}. $$ *)
(* In[9]: *)
transpose_for 2 [| [|1; 2|]; [|3; 4|] |];;
(* Notez qu'on peut faire mieux, sans boucles `for`, avec deux `Array.init` imbriqués : *)
(* In[10]: *)
let transpose p tab =
Array.init p (fun i -> (Array.init p (fun j -> tab.(j).(i))));;
(* In[11]: *)
transpose 2 [| [|1; 2|]; [|3; 4|] |];;
(* Et donc : *)
(* In[12]: *)
let carre_latin2 p t =
(contraintes_lignes p t) && (contraintes_lignes p (transpose p t))
;;
(* ### Un mauvais exemple *)
(* On va prendre le premier carré de taille $p = 3$ dans le problème de Su Doku donné en figure 1 de l'énoncé. *)
(*  *)
(* In[13]: *)
let p1 = 3;;
let t1 = [|
[| 1; 2; 7; |];
[| 3; 4; 9; |];
[| 5; 8; 6; |]
|];;
(* In[14]: *)
carre_latin p1 t1;;
(* $\implies$ Ce sous-carré de taille $p = 3$ n'est évidemment pas un "carré latin" : il contient des chiffres hors de $\{ 1, 2, 3 \}$ ! *)
(* ### Un bon exemple *)
(* On peut prendre un vrai exemple de taille $p = 3$, qui sera un carré latin. *)
(* In[15]: *)
let p2 = 3;;
let t2 = [|
[| 1; 2; 3 |];
[| 2; 3; 1 |];
[| 3; 1; 2 |]
|];;
(* In[16]: *)
carre_latin p2 t2;;
(* Les deux implémentations, la 1ère à base d'extraction de colonnes, la 2ème à base de transposée, donnent bien-sûr le même résultat ! *)
(* In[17]: *)
carre_latin2 p2 t2;;
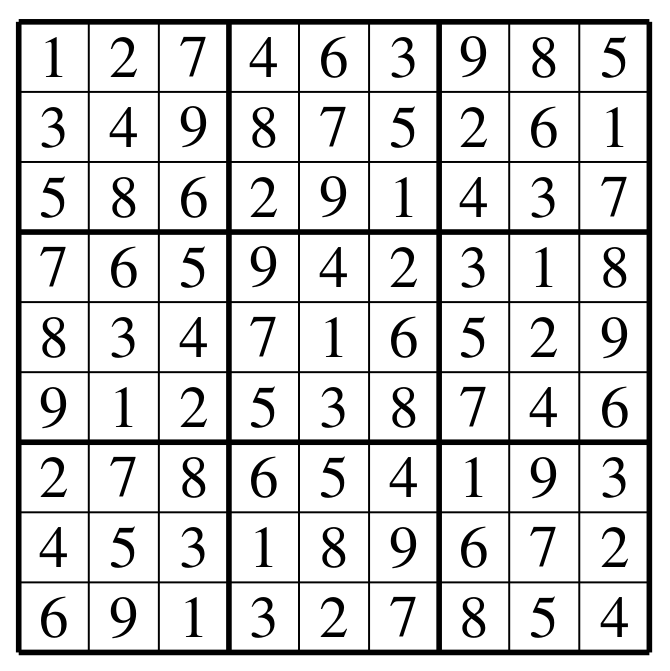
(* ### Un exemple de Su Doku de taille $9 \times 9$ au compte juste *)
(* Avec $p = n^2 = 9$, on reprend l'exemple du texte : *)
(*
*)
(* In[13]: *)
let p1 = 3;;
let t1 = [|
[| 1; 2; 7; |];
[| 3; 4; 9; |];
[| 5; 8; 6; |]
|];;
(* In[14]: *)
carre_latin p1 t1;;
(* $\implies$ Ce sous-carré de taille $p = 3$ n'est évidemment pas un "carré latin" : il contient des chiffres hors de $\{ 1, 2, 3 \}$ ! *)
(* ### Un bon exemple *)
(* On peut prendre un vrai exemple de taille $p = 3$, qui sera un carré latin. *)
(* In[15]: *)
let p2 = 3;;
let t2 = [|
[| 1; 2; 3 |];
[| 2; 3; 1 |];
[| 3; 1; 2 |]
|];;
(* In[16]: *)
carre_latin p2 t2;;
(* Les deux implémentations, la 1ère à base d'extraction de colonnes, la 2ème à base de transposée, donnent bien-sûr le même résultat ! *)
(* In[17]: *)
carre_latin2 p2 t2;;
(* ### Un exemple de Su Doku de taille $9 \times 9$ au compte juste *)
(* Avec $p = n^2 = 9$, on reprend l'exemple du texte : *)
(*  *)
(* Ça va être long un peu à écrire, mais au moins on vérifiera notre fonction sur un vrai exemple. *)
(* In[18]: *)
let p3 = 9 ;;
let t3 = [|
[| 1; 2; 7; 4; 6; 3; 9; 8; 5 |];
[| 3; 4; 9; 8; 7; 5; 2; 6; 1 |];
[| 5; 8; 6; 2; 9; 1; 4; 3; 7 |];
[| 7; 6; 5; 9; 4; 2; 3; 1; 8 |];
[| 8; 3; 4; 7; 1; 6; 5; 2; 9 |];
[| 9; 1; 2; 5; 3; 8; 7; 4; 6 |];
[| 2; 7; 8; 6; 5; 4; 1; 9; 3 |];
[| 4; 5; 3; 1; 8; 9; 6; 7; 2 |];
[| 6; 9; 1; 3; 2; 7; 8; 5; 4 |]
|];;
(* In[19]: *)
carre_latin p3 t3;;
(* In[20]: *)
carre_latin2 p3 t3;;
(* ### Un exemple de Su Doku au *comte* faux *)
(* Avec $p = n^2 = 9$, en modifiant seulement une case du tableau $T$ précédent. *)
(* In[21]: *)
let p4 = 9 ;;
let t4 = [|
[| 1; 2; 7; 4; 6; 3; 9; 8; 5 |];
[| 3; 4; 9; 8; 7; 5; 2; 6; 1 |];
[| 5; 8; 6; 2; 9; 1; 4; 3; 7 |];
[| 7; 6; 5; 9; 4; 2; 3; 1; 8 |];
[| 8; 2; 4; 7; 1; 6; 5; 2; 9 |]; (* Ligne non valable, 2 est là deux fois !*)
[| 9; 1; 2; 5; 3; 8; 7; 4; 6 |];
[| 2; 7; 8; 6; 5; 4; 1; 9; 3 |];
[| 4; 5; 3; 1; 8; 9; 6; 7; 2 |];
[| 6; 9; 1; 3; 2; 7; 8; 5; 4 |]
|];;
(* In[22]: *)
carre_latin p4 t4;;
(* In[23]: *)
carre_latin2 p4 t4;;
(* $\implies$ Notre fonction `carre_latin` semble bien marcher. *)
(* ### Un exemple de comte... Dooku ? *)
(* [](http://fr.starwars.wikia.com/wiki/Dooku) *)
(* > *Nan, je déconne*. *)
(* > ... Bien-sûr, évitez les blagues pourries le jour de l'oral ! *)
(* > Mais une bonne blague peut être bien reçue... *)
(* ## Vérifier les autres contraintes *)
(* En bonus, on peut écrire une fonction qui vérifie les contraintes sur les petits carrés en plus des contraintes sur les lignes et les colonnes. *)
(* On a déjà tout ce qu'il faut, il suffit d'écrire une fonction qui extraie un petit carré de taille $n \times n$ ($n = \sqrt{p}$). *)
(* In[24]: *)
let racine_carree i = int_of_float (sqrt (float_of_int i));;
(* C'est moins facile à écrire, mais on peut extraire un "petit carré" de taille $n \times n$, pour $t$ de taille $p \times p$, si $p = n^2$. *)
(* Ici, on extraie le $i$ème petit carré en ligne, et le $j$ème petit carré en colonne, *)
(* - en jouant avec des modulos et des divisions entières sur $k$ qui sera de $0$ à $p-1$ (`k / n` et `k mod n` font parcourir $0 \dots n-1$), *)
(* - et en jouant avec des multiplications sur `i` et `j`. *)
(* In[25]: *)
let petit_carre p n t i j =
Array.init p (fun k ->
t.(n*i + (k / n)).(n*j + (k mod n))
)
;;
(* > Bien-sûr, `p` et `n` pourraient ne pas être donnés à la fonction, mais autant se simplifier la vie ! *)
(* Par exemple, avec le tableau `t3` défini plus haut, et $p = 9 = n^2$ pour $n = 3$, on vérifie que les $9$ petits carrés arrivent dans l'ordre : *)
(* In[26]: *)
let n3 = racine_carree p3;;
(* In[27]: *)
petit_carre p3 n3 t3 0 0;;
petit_carre p3 n3 t3 0 1;;
petit_carre p3 n3 t3 0 2;;
petit_carre p3 n3 t3 1 0;;
petit_carre p3 n3 t3 1 1;;
petit_carre p3 n3 t3 1 2;;
petit_carre p3 n3 t3 2 0;;
petit_carre p3 n3 t3 2 1;;
petit_carre p3 n3 t3 2 2;;
(* Enfin, la contrainte supplémentaire s'écrit exactement comme les deux autres : *)
(* In[28]: *)
let petits_carres_sont_latins p t =
let n = racine_carree p in
(* Par flemme, on créé le tableau entier, qu'on vérifie après *)
let contraintes_petits_carres =
Array.init p (fun i ->
estNp p (petit_carre p n t (i / n) (i mod n) )
)
in
(* Mais on peut mieux faire, avec une boucle while par exemple, on sort dès qu'une contrainte est fausse *)
tousVrai contraintes_petits_carres
;;
(* $\implies$ Et on peut vérifier que le tableau `t3` satisfait bien cette contrainte : *)
(* In[29]: *)
petits_carres_sont_latins p3 t3;;
(* $\implies$ Et on peut vérifier que le tableau `t4` ne satisfait pas cette contrainte : *)
(* In[30]: *)
petits_carres_sont_latins p4 t4;;
(* ---- *)
(* ## Conclusion *)
(* Voilà pour la question obligatoire de programmation : *)
(* - on a décomposé le problème en sous-fonctions, *)
(* - on a essayé d'être fainéant, en réutilisant les sous-fonctions, *)
(* - on a fait des exemples et *on les garde* dans ce qu'on présente au jury, *)
(* - on a testé la fonction exigée sur de petits exemples et sur un exemple de taille réelle (venant du texte) *)
(* Et on a essayé de faire *un peu plus*, en implémentant la vérification d'une contrainte de plus. *)
(* > Bien-sûr, ce petit notebook ne se prétend pas être une solution optimale, ni exhaustive. *)
*)
(* Ça va être long un peu à écrire, mais au moins on vérifiera notre fonction sur un vrai exemple. *)
(* In[18]: *)
let p3 = 9 ;;
let t3 = [|
[| 1; 2; 7; 4; 6; 3; 9; 8; 5 |];
[| 3; 4; 9; 8; 7; 5; 2; 6; 1 |];
[| 5; 8; 6; 2; 9; 1; 4; 3; 7 |];
[| 7; 6; 5; 9; 4; 2; 3; 1; 8 |];
[| 8; 3; 4; 7; 1; 6; 5; 2; 9 |];
[| 9; 1; 2; 5; 3; 8; 7; 4; 6 |];
[| 2; 7; 8; 6; 5; 4; 1; 9; 3 |];
[| 4; 5; 3; 1; 8; 9; 6; 7; 2 |];
[| 6; 9; 1; 3; 2; 7; 8; 5; 4 |]
|];;
(* In[19]: *)
carre_latin p3 t3;;
(* In[20]: *)
carre_latin2 p3 t3;;
(* ### Un exemple de Su Doku au *comte* faux *)
(* Avec $p = n^2 = 9$, en modifiant seulement une case du tableau $T$ précédent. *)
(* In[21]: *)
let p4 = 9 ;;
let t4 = [|
[| 1; 2; 7; 4; 6; 3; 9; 8; 5 |];
[| 3; 4; 9; 8; 7; 5; 2; 6; 1 |];
[| 5; 8; 6; 2; 9; 1; 4; 3; 7 |];
[| 7; 6; 5; 9; 4; 2; 3; 1; 8 |];
[| 8; 2; 4; 7; 1; 6; 5; 2; 9 |]; (* Ligne non valable, 2 est là deux fois !*)
[| 9; 1; 2; 5; 3; 8; 7; 4; 6 |];
[| 2; 7; 8; 6; 5; 4; 1; 9; 3 |];
[| 4; 5; 3; 1; 8; 9; 6; 7; 2 |];
[| 6; 9; 1; 3; 2; 7; 8; 5; 4 |]
|];;
(* In[22]: *)
carre_latin p4 t4;;
(* In[23]: *)
carre_latin2 p4 t4;;
(* $\implies$ Notre fonction `carre_latin` semble bien marcher. *)
(* ### Un exemple de comte... Dooku ? *)
(* [](http://fr.starwars.wikia.com/wiki/Dooku) *)
(* > *Nan, je déconne*. *)
(* > ... Bien-sûr, évitez les blagues pourries le jour de l'oral ! *)
(* > Mais une bonne blague peut être bien reçue... *)
(* ## Vérifier les autres contraintes *)
(* En bonus, on peut écrire une fonction qui vérifie les contraintes sur les petits carrés en plus des contraintes sur les lignes et les colonnes. *)
(* On a déjà tout ce qu'il faut, il suffit d'écrire une fonction qui extraie un petit carré de taille $n \times n$ ($n = \sqrt{p}$). *)
(* In[24]: *)
let racine_carree i = int_of_float (sqrt (float_of_int i));;
(* C'est moins facile à écrire, mais on peut extraire un "petit carré" de taille $n \times n$, pour $t$ de taille $p \times p$, si $p = n^2$. *)
(* Ici, on extraie le $i$ème petit carré en ligne, et le $j$ème petit carré en colonne, *)
(* - en jouant avec des modulos et des divisions entières sur $k$ qui sera de $0$ à $p-1$ (`k / n` et `k mod n` font parcourir $0 \dots n-1$), *)
(* - et en jouant avec des multiplications sur `i` et `j`. *)
(* In[25]: *)
let petit_carre p n t i j =
Array.init p (fun k ->
t.(n*i + (k / n)).(n*j + (k mod n))
)
;;
(* > Bien-sûr, `p` et `n` pourraient ne pas être donnés à la fonction, mais autant se simplifier la vie ! *)
(* Par exemple, avec le tableau `t3` défini plus haut, et $p = 9 = n^2$ pour $n = 3$, on vérifie que les $9$ petits carrés arrivent dans l'ordre : *)
(* In[26]: *)
let n3 = racine_carree p3;;
(* In[27]: *)
petit_carre p3 n3 t3 0 0;;
petit_carre p3 n3 t3 0 1;;
petit_carre p3 n3 t3 0 2;;
petit_carre p3 n3 t3 1 0;;
petit_carre p3 n3 t3 1 1;;
petit_carre p3 n3 t3 1 2;;
petit_carre p3 n3 t3 2 0;;
petit_carre p3 n3 t3 2 1;;
petit_carre p3 n3 t3 2 2;;
(* Enfin, la contrainte supplémentaire s'écrit exactement comme les deux autres : *)
(* In[28]: *)
let petits_carres_sont_latins p t =
let n = racine_carree p in
(* Par flemme, on créé le tableau entier, qu'on vérifie après *)
let contraintes_petits_carres =
Array.init p (fun i ->
estNp p (petit_carre p n t (i / n) (i mod n) )
)
in
(* Mais on peut mieux faire, avec une boucle while par exemple, on sort dès qu'une contrainte est fausse *)
tousVrai contraintes_petits_carres
;;
(* $\implies$ Et on peut vérifier que le tableau `t3` satisfait bien cette contrainte : *)
(* In[29]: *)
petits_carres_sont_latins p3 t3;;
(* $\implies$ Et on peut vérifier que le tableau `t4` ne satisfait pas cette contrainte : *)
(* In[30]: *)
petits_carres_sont_latins p4 t4;;
(* ---- *)
(* ## Conclusion *)
(* Voilà pour la question obligatoire de programmation : *)
(* - on a décomposé le problème en sous-fonctions, *)
(* - on a essayé d'être fainéant, en réutilisant les sous-fonctions, *)
(* - on a fait des exemples et *on les garde* dans ce qu'on présente au jury, *)
(* - on a testé la fonction exigée sur de petits exemples et sur un exemple de taille réelle (venant du texte) *)
(* Et on a essayé de faire *un peu plus*, en implémentant la vérification d'une contrainte de plus. *)
(* > Bien-sûr, ce petit notebook ne se prétend pas être une solution optimale, ni exhaustive. *)
 *)
(* In[13]: *)
let p1 = 3;;
let t1 = [|
[| 1; 2; 7; |];
[| 3; 4; 9; |];
[| 5; 8; 6; |]
|];;
(* In[14]: *)
carre_latin p1 t1;;
(* $\implies$ Ce sous-carré de taille $p = 3$ n'est évidemment pas un "carré latin" : il contient des chiffres hors de $\{ 1, 2, 3 \}$ ! *)
(* ### Un bon exemple *)
(* On peut prendre un vrai exemple de taille $p = 3$, qui sera un carré latin. *)
(* In[15]: *)
let p2 = 3;;
let t2 = [|
[| 1; 2; 3 |];
[| 2; 3; 1 |];
[| 3; 1; 2 |]
|];;
(* In[16]: *)
carre_latin p2 t2;;
(* Les deux implémentations, la 1ère à base d'extraction de colonnes, la 2ème à base de transposée, donnent bien-sûr le même résultat ! *)
(* In[17]: *)
carre_latin2 p2 t2;;
(* ### Un exemple de Su Doku de taille $9 \times 9$ au compte juste *)
(* Avec $p = n^2 = 9$, on reprend l'exemple du texte : *)
(*
*)
(* In[13]: *)
let p1 = 3;;
let t1 = [|
[| 1; 2; 7; |];
[| 3; 4; 9; |];
[| 5; 8; 6; |]
|];;
(* In[14]: *)
carre_latin p1 t1;;
(* $\implies$ Ce sous-carré de taille $p = 3$ n'est évidemment pas un "carré latin" : il contient des chiffres hors de $\{ 1, 2, 3 \}$ ! *)
(* ### Un bon exemple *)
(* On peut prendre un vrai exemple de taille $p = 3$, qui sera un carré latin. *)
(* In[15]: *)
let p2 = 3;;
let t2 = [|
[| 1; 2; 3 |];
[| 2; 3; 1 |];
[| 3; 1; 2 |]
|];;
(* In[16]: *)
carre_latin p2 t2;;
(* Les deux implémentations, la 1ère à base d'extraction de colonnes, la 2ème à base de transposée, donnent bien-sûr le même résultat ! *)
(* In[17]: *)
carre_latin2 p2 t2;;
(* ### Un exemple de Su Doku de taille $9 \times 9$ au compte juste *)
(* Avec $p = n^2 = 9$, on reprend l'exemple du texte : *)
(*  *)
(* Ça va être long un peu à écrire, mais au moins on vérifiera notre fonction sur un vrai exemple. *)
(* In[18]: *)
let p3 = 9 ;;
let t3 = [|
[| 1; 2; 7; 4; 6; 3; 9; 8; 5 |];
[| 3; 4; 9; 8; 7; 5; 2; 6; 1 |];
[| 5; 8; 6; 2; 9; 1; 4; 3; 7 |];
[| 7; 6; 5; 9; 4; 2; 3; 1; 8 |];
[| 8; 3; 4; 7; 1; 6; 5; 2; 9 |];
[| 9; 1; 2; 5; 3; 8; 7; 4; 6 |];
[| 2; 7; 8; 6; 5; 4; 1; 9; 3 |];
[| 4; 5; 3; 1; 8; 9; 6; 7; 2 |];
[| 6; 9; 1; 3; 2; 7; 8; 5; 4 |]
|];;
(* In[19]: *)
carre_latin p3 t3;;
(* In[20]: *)
carre_latin2 p3 t3;;
(* ### Un exemple de Su Doku au *comte* faux *)
(* Avec $p = n^2 = 9$, en modifiant seulement une case du tableau $T$ précédent. *)
(* In[21]: *)
let p4 = 9 ;;
let t4 = [|
[| 1; 2; 7; 4; 6; 3; 9; 8; 5 |];
[| 3; 4; 9; 8; 7; 5; 2; 6; 1 |];
[| 5; 8; 6; 2; 9; 1; 4; 3; 7 |];
[| 7; 6; 5; 9; 4; 2; 3; 1; 8 |];
[| 8; 2; 4; 7; 1; 6; 5; 2; 9 |]; (* Ligne non valable, 2 est là deux fois !*)
[| 9; 1; 2; 5; 3; 8; 7; 4; 6 |];
[| 2; 7; 8; 6; 5; 4; 1; 9; 3 |];
[| 4; 5; 3; 1; 8; 9; 6; 7; 2 |];
[| 6; 9; 1; 3; 2; 7; 8; 5; 4 |]
|];;
(* In[22]: *)
carre_latin p4 t4;;
(* In[23]: *)
carre_latin2 p4 t4;;
(* $\implies$ Notre fonction `carre_latin` semble bien marcher. *)
(* ### Un exemple de comte... Dooku ? *)
(* [](http://fr.starwars.wikia.com/wiki/Dooku) *)
(* > *Nan, je déconne*. *)
(* > ... Bien-sûr, évitez les blagues pourries le jour de l'oral ! *)
(* > Mais une bonne blague peut être bien reçue... *)
(* ## Vérifier les autres contraintes *)
(* En bonus, on peut écrire une fonction qui vérifie les contraintes sur les petits carrés en plus des contraintes sur les lignes et les colonnes. *)
(* On a déjà tout ce qu'il faut, il suffit d'écrire une fonction qui extraie un petit carré de taille $n \times n$ ($n = \sqrt{p}$). *)
(* In[24]: *)
let racine_carree i = int_of_float (sqrt (float_of_int i));;
(* C'est moins facile à écrire, mais on peut extraire un "petit carré" de taille $n \times n$, pour $t$ de taille $p \times p$, si $p = n^2$. *)
(* Ici, on extraie le $i$ème petit carré en ligne, et le $j$ème petit carré en colonne, *)
(* - en jouant avec des modulos et des divisions entières sur $k$ qui sera de $0$ à $p-1$ (`k / n` et `k mod n` font parcourir $0 \dots n-1$), *)
(* - et en jouant avec des multiplications sur `i` et `j`. *)
(* In[25]: *)
let petit_carre p n t i j =
Array.init p (fun k ->
t.(n*i + (k / n)).(n*j + (k mod n))
)
;;
(* > Bien-sûr, `p` et `n` pourraient ne pas être donnés à la fonction, mais autant se simplifier la vie ! *)
(* Par exemple, avec le tableau `t3` défini plus haut, et $p = 9 = n^2$ pour $n = 3$, on vérifie que les $9$ petits carrés arrivent dans l'ordre : *)
(* In[26]: *)
let n3 = racine_carree p3;;
(* In[27]: *)
petit_carre p3 n3 t3 0 0;;
petit_carre p3 n3 t3 0 1;;
petit_carre p3 n3 t3 0 2;;
petit_carre p3 n3 t3 1 0;;
petit_carre p3 n3 t3 1 1;;
petit_carre p3 n3 t3 1 2;;
petit_carre p3 n3 t3 2 0;;
petit_carre p3 n3 t3 2 1;;
petit_carre p3 n3 t3 2 2;;
(* Enfin, la contrainte supplémentaire s'écrit exactement comme les deux autres : *)
(* In[28]: *)
let petits_carres_sont_latins p t =
let n = racine_carree p in
(* Par flemme, on créé le tableau entier, qu'on vérifie après *)
let contraintes_petits_carres =
Array.init p (fun i ->
estNp p (petit_carre p n t (i / n) (i mod n) )
)
in
(* Mais on peut mieux faire, avec une boucle while par exemple, on sort dès qu'une contrainte est fausse *)
tousVrai contraintes_petits_carres
;;
(* $\implies$ Et on peut vérifier que le tableau `t3` satisfait bien cette contrainte : *)
(* In[29]: *)
petits_carres_sont_latins p3 t3;;
(* $\implies$ Et on peut vérifier que le tableau `t4` ne satisfait pas cette contrainte : *)
(* In[30]: *)
petits_carres_sont_latins p4 t4;;
(* ---- *)
(* ## Conclusion *)
(* Voilà pour la question obligatoire de programmation : *)
(* - on a décomposé le problème en sous-fonctions, *)
(* - on a essayé d'être fainéant, en réutilisant les sous-fonctions, *)
(* - on a fait des exemples et *on les garde* dans ce qu'on présente au jury, *)
(* - on a testé la fonction exigée sur de petits exemples et sur un exemple de taille réelle (venant du texte) *)
(* Et on a essayé de faire *un peu plus*, en implémentant la vérification d'une contrainte de plus. *)
(* > Bien-sûr, ce petit notebook ne se prétend pas être une solution optimale, ni exhaustive. *)
*)
(* Ça va être long un peu à écrire, mais au moins on vérifiera notre fonction sur un vrai exemple. *)
(* In[18]: *)
let p3 = 9 ;;
let t3 = [|
[| 1; 2; 7; 4; 6; 3; 9; 8; 5 |];
[| 3; 4; 9; 8; 7; 5; 2; 6; 1 |];
[| 5; 8; 6; 2; 9; 1; 4; 3; 7 |];
[| 7; 6; 5; 9; 4; 2; 3; 1; 8 |];
[| 8; 3; 4; 7; 1; 6; 5; 2; 9 |];
[| 9; 1; 2; 5; 3; 8; 7; 4; 6 |];
[| 2; 7; 8; 6; 5; 4; 1; 9; 3 |];
[| 4; 5; 3; 1; 8; 9; 6; 7; 2 |];
[| 6; 9; 1; 3; 2; 7; 8; 5; 4 |]
|];;
(* In[19]: *)
carre_latin p3 t3;;
(* In[20]: *)
carre_latin2 p3 t3;;
(* ### Un exemple de Su Doku au *comte* faux *)
(* Avec $p = n^2 = 9$, en modifiant seulement une case du tableau $T$ précédent. *)
(* In[21]: *)
let p4 = 9 ;;
let t4 = [|
[| 1; 2; 7; 4; 6; 3; 9; 8; 5 |];
[| 3; 4; 9; 8; 7; 5; 2; 6; 1 |];
[| 5; 8; 6; 2; 9; 1; 4; 3; 7 |];
[| 7; 6; 5; 9; 4; 2; 3; 1; 8 |];
[| 8; 2; 4; 7; 1; 6; 5; 2; 9 |]; (* Ligne non valable, 2 est là deux fois !*)
[| 9; 1; 2; 5; 3; 8; 7; 4; 6 |];
[| 2; 7; 8; 6; 5; 4; 1; 9; 3 |];
[| 4; 5; 3; 1; 8; 9; 6; 7; 2 |];
[| 6; 9; 1; 3; 2; 7; 8; 5; 4 |]
|];;
(* In[22]: *)
carre_latin p4 t4;;
(* In[23]: *)
carre_latin2 p4 t4;;
(* $\implies$ Notre fonction `carre_latin` semble bien marcher. *)
(* ### Un exemple de comte... Dooku ? *)
(* [](http://fr.starwars.wikia.com/wiki/Dooku) *)
(* > *Nan, je déconne*. *)
(* > ... Bien-sûr, évitez les blagues pourries le jour de l'oral ! *)
(* > Mais une bonne blague peut être bien reçue... *)
(* ## Vérifier les autres contraintes *)
(* En bonus, on peut écrire une fonction qui vérifie les contraintes sur les petits carrés en plus des contraintes sur les lignes et les colonnes. *)
(* On a déjà tout ce qu'il faut, il suffit d'écrire une fonction qui extraie un petit carré de taille $n \times n$ ($n = \sqrt{p}$). *)
(* In[24]: *)
let racine_carree i = int_of_float (sqrt (float_of_int i));;
(* C'est moins facile à écrire, mais on peut extraire un "petit carré" de taille $n \times n$, pour $t$ de taille $p \times p$, si $p = n^2$. *)
(* Ici, on extraie le $i$ème petit carré en ligne, et le $j$ème petit carré en colonne, *)
(* - en jouant avec des modulos et des divisions entières sur $k$ qui sera de $0$ à $p-1$ (`k / n` et `k mod n` font parcourir $0 \dots n-1$), *)
(* - et en jouant avec des multiplications sur `i` et `j`. *)
(* In[25]: *)
let petit_carre p n t i j =
Array.init p (fun k ->
t.(n*i + (k / n)).(n*j + (k mod n))
)
;;
(* > Bien-sûr, `p` et `n` pourraient ne pas être donnés à la fonction, mais autant se simplifier la vie ! *)
(* Par exemple, avec le tableau `t3` défini plus haut, et $p = 9 = n^2$ pour $n = 3$, on vérifie que les $9$ petits carrés arrivent dans l'ordre : *)
(* In[26]: *)
let n3 = racine_carree p3;;
(* In[27]: *)
petit_carre p3 n3 t3 0 0;;
petit_carre p3 n3 t3 0 1;;
petit_carre p3 n3 t3 0 2;;
petit_carre p3 n3 t3 1 0;;
petit_carre p3 n3 t3 1 1;;
petit_carre p3 n3 t3 1 2;;
petit_carre p3 n3 t3 2 0;;
petit_carre p3 n3 t3 2 1;;
petit_carre p3 n3 t3 2 2;;
(* Enfin, la contrainte supplémentaire s'écrit exactement comme les deux autres : *)
(* In[28]: *)
let petits_carres_sont_latins p t =
let n = racine_carree p in
(* Par flemme, on créé le tableau entier, qu'on vérifie après *)
let contraintes_petits_carres =
Array.init p (fun i ->
estNp p (petit_carre p n t (i / n) (i mod n) )
)
in
(* Mais on peut mieux faire, avec une boucle while par exemple, on sort dès qu'une contrainte est fausse *)
tousVrai contraintes_petits_carres
;;
(* $\implies$ Et on peut vérifier que le tableau `t3` satisfait bien cette contrainte : *)
(* In[29]: *)
petits_carres_sont_latins p3 t3;;
(* $\implies$ Et on peut vérifier que le tableau `t4` ne satisfait pas cette contrainte : *)
(* In[30]: *)
petits_carres_sont_latins p4 t4;;
(* ---- *)
(* ## Conclusion *)
(* Voilà pour la question obligatoire de programmation : *)
(* - on a décomposé le problème en sous-fonctions, *)
(* - on a essayé d'être fainéant, en réutilisant les sous-fonctions, *)
(* - on a fait des exemples et *on les garde* dans ce qu'on présente au jury, *)
(* - on a testé la fonction exigée sur de petits exemples et sur un exemple de taille réelle (venant du texte) *)
(* Et on a essayé de faire *un peu plus*, en implémentant la vérification d'une contrainte de plus. *)
(* > Bien-sûr, ce petit notebook ne se prétend pas être une solution optimale, ni exhaustive. *)