Table of Contents

1  Texte d'oral de modélisation - Agrégation Option Informatique
1.1  Préparation à l'agrégation - ENS de Rennes, 2016-17
1.2  À propos de ce document
1.3  Question de programmation
1.4  Réponse à l'exercice requis
1.4.1  Une autre approche
1.4.2  Un mauvais exemple
1.4.3  Un bon exemple
1.4.4  Un exemple de Su Doku de taille $9 \times 9$ au compte juste
1.4.5  Un exemple de Su Doku au comte faux
1.4.6  Un exemple de comte... Dooku ?
1.5  Vérifier les autres contraintes
1.6  Conclusion

Texte d'oral de modélisation - Agrégation Option Informatique

Préparation à l'agrégation - ENS de Rennes, 2016-17

  • Date : 3 avril 2017
  • Auteur : Lilian Besson
  • Texte: Annale 2006, "Sudoku"

À propos de ce document

In [1]:
Sys.command "ocaml -version";;

The OCaml toplevel, version 4.02.3
Out[1]:
- : int = 0

Question de programmation

La question de programmation pour ce texte était donnée au tout début, en page 2 :

« Écrire une fonction prenant pour paramètres un entier, $p \geq 1$, et un tableau carré de côté $p$ (donc de taille $p^2$) d'entiers, $T$, et renvoyant un booléen disant si ce tableau est un carré latin, c'est-à-dire contenant dans chaque ligne et chaque colonne une et une seule fois chaque entier de $1$ à $p$.

Mathématiquement, si $N_p := \{1,\dots,p\}$, cela donne un prédicat $\mathrm{estCarreLatin}_p(T)$ sur un tableau $T$ : $$ \mathrm{estCarreLatin}_p(T) \Longleftrightarrow \forall i \in N_p, \left\{ T_{i,j} : j \in N_p \right\} = N_p \;\text{and}\; \forall j \in N_p, \left\{ T_{i,j} : i \in N_p \right\} = N_p $$

« En prenant $p = n^2$ on obtient une partie des contraintes d'admissibilité d'une grille complète de Su Doku, mais il reste encore à vérifier la contrainte sur les petits carrés. »

Pour l'annecdote historique, cette idée de carré latin date vraiment de l'époque romaine antique. On a trouvé à Pompeï des carrés latins de taille $4$ ou $5$ !

Réponse à l'exercice requis

C'est assez rapide :

  1. On écrit une fonction qui permet d'extraire une ligne ou une colonne d'un tableau $T$,
  2. On écrit ensuite une fonction qui permet de vérifier si un tableau de $p$ entiers contient exactement $N_p = \{1, \dots, p\}$,
  3. Enfin, on vérifie toutes les contraintes.

Remarque: On suppose que tous les tableaux considérés sont :

  • non vides
  • et carrés On ne vérifie pas ces deux points.
In [2]:
let ligne p t i = Array.init p (fun j -> t.(i).(j)) ;;
(* t.(i) marche aussi bien ! *)

let colonne p t j = Array.init p (fun i -> t.(i).(j)) ;;
Out[2]:
val ligne : int -> 'a array array -> int -> 'a array = <fun>
Out[2]:
val colonne : int -> 'a array array -> int -> 'a array = <fun>

On a besoin de savoir si un tableau de booléens sont tous vrais ou pas. On peut utiliser la fonction déjà existante, Array.for_all, ou bien un Array.fold_left, ou une implémentation manuelle.

In [3]:
let tousVrai tab =
    let res = ref true in
    for i = 0 to (Array.length tab) - 1 do
        res := !res && tab.(i)
    done;
    !res
;;
Out[3]:
val tousVrai : bool array -> bool = <fun>
In [4]:
let tousVrai = Array.fold_left (&&) true;;
(* Array.for_all marche aussi bien ! *)
Out[4]:
val tousVrai : bool array -> bool = <fun>

Ca permet de facilement vérifier si un tableau tab de taille $p$ est exactement $N_p = \{1,\dots,p\}$, en temps linéaire (c'est optimal) en $p$.

  1. On ajoute un test que tous les entiers soient bien entre $1$ et $p$,
  2. puis on fait ce test en $\mathcal{O}(\# tab)$, en créant est un tableau estLa de taille $p$, remplis de false. En bouclant sur $t$, on remplit $\texttt{tab}[i]$ à true dans estLa (en fait, tab(i) - 1 car les indices sont entre $0$ et $p-1$). A la fin, si le tableau estLa est rempli de true, alors on a vu tous les entiers de $N_p$ une et une seule fois.
In [5]:
let estNp p tab =
    if tousVrai (Array.map (fun x -> (1 <= x) && (x <= p)) tab) then begin 
        let estLa = Array.make p false in
        for i = 0 to p - 1 do
            estLa.(tab.(i) - 1) <- true
        done;
        tousVrai estLa
    end
    else
        false
;;
Out[5]:
val estNp : int -> int array -> bool = <fun>

On va adopter une méthode naïve mais simple à écrire :

  • on construit deux tableaux de $p$ booléens,
  • on les remplit des contraintes pour les $p$ lignes et les $p$ colonnes,
  • et on les vérifie avec tousVrai.
In [32]:
let contraintes_lignes p t =
    tousVrai (Array.init p (fun i ->
            estNp p (ligne p t i)
        ))
;;
Out[32]:
val contraintes_lignes : int -> int array array -> bool = <fun>
In [31]:
let contraintes_colonnes p t =
    tousVrai (Array.init p (fun j ->
            estNp p (colonne p t j)
        ))
;;
Out[31]:
val contraintes_colonnes : int -> int array array -> bool = <fun>
In [7]:
let carre_latin p t =
    (contraintes_lignes p t) && (contraintes_colonnes p t)
;;
Out[7]:
val carre_latin : int -> int array array -> bool = <fun>

Une autre approche

Plutôt que d'écrire une fonction pour extraire une colonne, et deux fonction qui vérifies les contraintes sur les lignes et les colonnes, on remarque le fait suivant :

« Les colonnes de $t$ sont les lignes de $t^T$, la matrice transposée de $t$ ».

Donc pas besoin de savoir extraire les colonnes, dès qu'on a écrit contraintes_lignes, on peut avoir les contraintes sur les colonnes facilement.

Pour calculer la transposée, une approche simple utilise deux boucles for :

In [8]:
let transpose_for p tab =
    let tab2 = Array.make_matrix p p 0 in
    for i = 0 to p - 1 do
        for j = 0 to p - 1 do
            tab2.(i).(j) <- tab.(j).(i);
        done;
    done;
    tab2
;;
Out[8]:
val transpose_for : int -> int array array -> int array array = <fun>

On peut rapidement vérifier sur un exemple, $$ \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}^{T} = \begin{bmatrix} 1 & 3 \\ 2 & 4 \end{bmatrix}. $$

In [9]:
transpose_for 2 [| [|1; 2|]; [|3; 4|] |];;
Out[9]:
- : int array array = [|[|1; 3|]; [|2; 4|]|]

Notez qu'on peut faire mieux, sans boucles for, avec deux Array.init imbriqués :

In [10]:
let transpose p tab =
    Array.init p (fun i -> (Array.init p (fun j -> tab.(j).(i))));;
Out[10]:
val transpose : int -> 'a array array -> 'a array array = <fun>
In [11]:
transpose 2 [| [|1; 2|]; [|3; 4|] |];;
Out[11]:
- : int array array = [|[|1; 3|]; [|2; 4|]|]

Et donc :

In [12]:
let carre_latin2 p t =
    (contraintes_lignes p t) && (contraintes_lignes p (transpose p t))
;;
Out[12]:
val carre_latin2 : int -> int array array -> bool = <fun>

Un mauvais exemple

On va prendre le premier carré de taille $p = 3$ dans le problème de Su Doku donné en figure 1 de l'énoncé.

images/sudoku.png

In [13]:
let p1 = 3;;
let t1 = [|
    [| 1; 2; 7; |];
    [| 3; 4; 9; |];
    [| 5; 8; 6; |];
|];;
Out[13]:
val p1 : int = 3
Out[13]:
val t1 : int array array = [|[|1; 2; 7|]; [|3; 4; 9|]; [|5; 8; 6|]|]
In [14]:
carre_latin p1 t1;;
Out[14]:
- : bool = false

$\implies$ Ce sous-carré de taille $p = 3$ n'est évidemment pas un "carré latin" : il contient des chiffres hors de $\{ 1, 2, 3 \}$ !

Un bon exemple

On peut prendre un vrai exemple de taille $p = 3$, qui sera un carré latin.

In [15]:
let p2 = 3;;
let t2 = [|
    [| 1; 2; 3 |];
    [| 2; 3; 1 |];
    [| 3; 1; 2 |];
|];;
Out[15]:
val p2 : int = 3
Out[15]:
val t2 : int array array = [|[|1; 2; 3|]; [|2; 3; 1|]; [|3; 1; 2|]|]
In [16]:
carre_latin p2 t2;;
Out[16]:
- : bool = true

Les deux implémentations, la 1ère à base d'extraction de colonnes, la 2ème à base de transposée, donnent bien-sûr le même résultat !

In [17]:
carre_latin2 p2 t2;;
Out[17]:
- : bool = true

Un exemple de Su Doku de taille $9 \times 9$ au compte juste

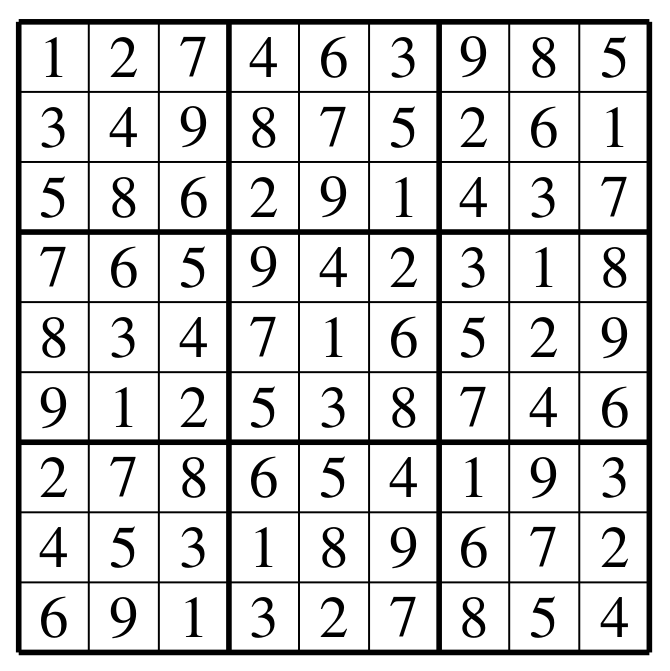
Avec $p = n^2 = 9$, on reprend l'exemple du texte : images/sudoku.png

Ça va être long un peu à écrire, mais au moins on vérifiera notre fonction sur un vrai exemple.

In [18]:
let p3 = 9 ;;
let t3 = [|
    [| 1; 2; 7; 4; 6; 3; 9; 8; 5 |];
    [| 3; 4; 9; 8; 7; 5; 2; 6; 1 |];
    [| 5; 8; 6; 2; 9; 1; 4; 3; 7 |];
    [| 7; 6; 5; 9; 4; 2; 3; 1; 8 |];
    [| 8; 3; 4; 7; 1; 6; 5; 2; 9 |];
    [| 9; 1; 2; 5; 3; 8; 7; 4; 6 |];
    [| 2; 7; 8; 6; 5; 4; 1; 9; 3 |];
    [| 4; 5; 3; 1; 8; 9; 6; 7; 2 |];
    [| 6; 9; 1; 3; 2; 7; 8; 5; 4 |];
|];
Out[18]:
val p3 : int = 9
Out[18]:
val t3 : int array array =
  [|[|1; 2; 7; 4; 6; 3; 9; 8; 5|]; [|3; 4; 9; 8; 7; 5; 2; 6; 1|];
    [|5; 8; 6; 2; 9; 1; 4; 3; 7|]; [|7; 6; 5; 9; 4; 2; 3; 1; 8|];
    [|8; 3; 4; 7; 1; 6; 5; 2; 9|]; [|9; 1; 2; 5; 3; 8; 7; 4; 6|];
    [|2; 7; 8; 6; 5; 4; 1; 9; 3|]; [|4; 5; 3; 1; 8; 9; 6; 7; 2|];
    [|6; 9; 1; 3; 2; 7; 8; 5; 4|]|]
In [19]:
carre_latin p3 t3;;
Out[19]:
- : bool = true
In [20]:
carre_latin2 p3 t3;;
Out[20]:
- : bool = true

Un exemple de Su Doku au comte faux

Avec $p = n^2 = 9$, en modifiant seulement une case du tableau $T$ précédent.

In [21]:
let p4 = 9 ;;
let t4 = [|
    [| 1; 2; 7; 4; 6; 3; 9; 8; 5 |];
    [| 3; 4; 9; 8; 7; 5; 2; 6; 1 |];
    [| 5; 8; 6; 2; 9; 1; 4; 3; 7 |];
    [| 7; 6; 5; 9; 4; 2; 3; 1; 8 |];
    [| 8; 2; 4; 7; 1; 6; 5; 2; 9 |]; (* Ligne non valable, 2 est là deux fois !*)
    [| 9; 1; 2; 5; 3; 8; 7; 4; 6 |];
    [| 2; 7; 8; 6; 5; 4; 1; 9; 3 |];
    [| 4; 5; 3; 1; 8; 9; 6; 7; 2 |];
    [| 6; 9; 1; 3; 2; 7; 8; 5; 4 |];
|];
Out[21]:
val p4 : int = 9
Out[21]:
val t4 : int array array =
  [|[|1; 2; 7; 4; 6; 3; 9; 8; 5|]; [|3; 4; 9; 8; 7; 5; 2; 6; 1|];
    [|5; 8; 6; 2; 9; 1; 4; 3; 7|]; [|7; 6; 5; 9; 4; 2; 3; 1; 8|];
    [|8; 2; 4; 7; 1; 6; 5; 2; 9|]; [|9; 1; 2; 5; 3; 8; 7; 4; 6|];
    [|2; 7; 8; 6; 5; 4; 1; 9; 3|]; [|4; 5; 3; 1; 8; 9; 6; 7; 2|];
    [|6; 9; 1; 3; 2; 7; 8; 5; 4|]|]
In [22]:
carre_latin p4 t4;;
Out[22]:
- : bool = false
In [23]:
carre_latin2 p4 t4;;
Out[23]:
- : bool = false

$\implies$ Notre fonction carre_latin semble bien marcher.

Un exemple de comte... Dooku ?

http://fr.starwars.wikia.com/wiki/Dooku ?

Nan, je déconne. ... Bien-sûr, évitez les blagues pourries le jour de l'oral ! Mais une bonne blague peut être bien reçue...

Vérifier les autres contraintes

En bonus, on peut écrire une fonction qui vérifie les contraintes sur les petits carrés en plus des contraintes sur les lignes et les colonnes.

On a déjà tout ce qu'il faut, il suffit d'écrire une fonction qui extraie un petit carré de taille $n \times n$ ($n = \sqrt{p}$).

In [24]:
let racine_carree i = int_of_float (sqrt (float_of_int i));;
Out[24]:
val racine_carree : int -> int = <fun>

C'est moins facile à écrire, mais on peut extraire un "petit carré" de taille $n \times n$, pour $t$ de taille $p \times p$, si $p = n^2$. Ici, on extraie le $i$ème petit carré en ligne, et le $j$ème petit carré en colonne,

  • en jouant avec des modulos et des divisions entières sur $k$ qui sera de $0$ à $p-1$ (k / n et k mod n font parcourir $0 \dots n-1$),
  • et en jouant avec des multiplications sur i et j.
In [25]:
let petit_carre p n t i j =
    Array.init p (fun k ->
        t.(n*i + (k / n)).(n*j + (k mod n))
    )
;;
Out[25]:
val petit_carre : int -> int -> 'a array array -> int -> int -> 'a array =
  <fun>

Bien-sûr, p et n pourraient ne pas être donnés à la fonction, mais autant se simplifier la vie !

Par exemple, avec le tableau t3 défini plus haut, et $p = 9 = n^2$ pour $n = 3$, on vérifie que les $9$ petits carrés arrivent dans l'ordre :

In [26]:
let n3 = racine_carree p3;;
Out[26]:
val n3 : int = 3
In [27]:
petit_carre p3 n3 t3 0 0;;
petit_carre p3 n3 t3 0 1;;
petit_carre p3 n3 t3 0 2;;
petit_carre p3 n3 t3 1 0;;
petit_carre p3 n3 t3 1 1;;
petit_carre p3 n3 t3 1 2;;
petit_carre p3 n3 t3 2 0;;
petit_carre p3 n3 t3 2 1;;
petit_carre p3 n3 t3 2 2;;
Out[27]:
- : int array = [|1; 2; 7; 3; 4; 9; 5; 8; 6|]
Out[27]:
- : int array = [|4; 6; 3; 8; 7; 5; 2; 9; 1|]
Out[27]:
- : int array = [|9; 8; 5; 2; 6; 1; 4; 3; 7|]
Out[27]:
- : int array = [|7; 6; 5; 8; 3; 4; 9; 1; 2|]
Out[27]:
- : int array = [|9; 4; 2; 7; 1; 6; 5; 3; 8|]
Out[27]:
- : int array = [|3; 1; 8; 5; 2; 9; 7; 4; 6|]
Out[27]:
- : int array = [|2; 7; 8; 4; 5; 3; 6; 9; 1|]
Out[27]:
- : int array = [|6; 5; 4; 1; 8; 9; 3; 2; 7|]
Out[27]:
- : int array = [|1; 9; 3; 6; 7; 2; 8; 5; 4|]

Enfin, la contrainte supplémentaire s'écrit exactement comme les deux autres :

In [28]:
let petits_carres_sont_latins p t =
    let n = racine_carree p in
    (* Par flemme, on créé le tableau entier, qu'on vérifie après *)
    let contraintes_petits_carres =
        Array.init p (fun i ->
            estNp p (petit_carre p n t (i / n) (i mod n) )
        )
    in
    (* Mais on peut mieux faire, avec une boucle while par exemple, on sort dès qu'une contrainte est fausse *)
    tousVrai contraintes_petits_carres
;;
Out[28]:
val petits_carres_sont_latins : int -> int array array -> bool = <fun>

$\implies$ Et on peut vérifier que le tableau t3 satisfait bien cette contrainte :

In [29]:
petits_carres_sont_latins p3 t3;;
Out[29]:
- : bool = true

$\implies$ Et on peut vérifier que le tableau t4 ne satisfait pas cette contrainte :

In [30]:
petits_carres_sont_latins p4 t4;;
Out[30]:
- : bool = false

Conclusion

Voilà pour la question obligatoire de programmation :

  • on a décomposé le problème en sous-fonctions,
  • on a essayé d'être fainéant, en réutilisant les sous-fonctions,
  • on a fait des exemples et on les garde dans ce qu'on présente au jury,
  • on a testé la fonction exigée sur de petits exemples et sur un exemple de taille réelle (venant du texte)

Et on a essayé de faire un peu plus, en implémentant la vérification d'une contrainte de plus.

Bien-sûr, ce petit notebook ne se prétend pas être une solution optimale, ni exhaustive.