Upper-Confidence Bound for Frequency Selection in IoT Networks with Retransmissions
Abstract
Internet of Things (IoT) and in particular Low Power Wide Area (LPWA) technologies are being developed to enable long-range Machine-to-Machine (M2M) communications. It is considered a main driver for a vast variety of applications, where the need to fit a growing number of end-devices requires to design novel and more efficient access schemes. For instance, in smart grid communications, simple access schemes lead us to an increase of the latency, the number of collisions, and the power consumption. We consider devices communicate with the gateway using a wireless ALOHA-based protocol, and taking as inputs for the learning process, the number of successful transmitted packets and retransmissions. In this article, we propose and evaluate different learning strategies based on Multi-Arm Bandit (MAB) algorithms that allow the devices to improve their access to the network, while taking into account the impact of encountered collisions. Our heuristics try to retransmit in a different channel in case of collision in a channel first chosen by a UCB algorithm, a well-known MAB strategy. Empirical results show that approaches based UCB obtain a significant improvement in terms of successful transmission probabilities, even if the naive UCB is good and outperforms other strategies.
I Introduction
Nowadays, the Internet of Things (IoT) is considered a promising technology that will support the communications among a large number of devices, as it has become evident with the increasing demand of smart grids and smart cities projects. Nevertheless, the development of IoT networks also require the redesign of the entire paradigm of the legacy technology, since new research aspects such as the lower power consumption and low signaling need to be considered.
In this context, the LPWAN [15] technology has been conceived for providing the aforementioned features. For instance, LoRaWAN and SigFox technologies have been adopted in the monitoring of large scale systems (e.g., smart grids), where a large number of devices compete for the transmission of their packets, in unlicensed ISM bands (e.g., MHz in Europe). Then, the improvement of the network performance in these unlicensed bands require to conceive novel MAC mechanisms.
One important concern in the MAC design is to reduce the Packet Loss Ratio (PLR) due to the interference caused by the collisions among the devices within the network and those following different standards. In fact, the number of collisions increases as more devices without coordination share the same band. Hence, novel access mechanisms considering the collisions need to be addressed to avoid degrading the network performance, while at the same time targeting features of IoT networks.
In this regard, Multi-Arm Bandit (MAB) algorithms [9] have been recently proposed as a solution and in particular in LPWA networks [8, 4, 7]. For instance in [7], the non-stationarity introduced by the presence of more than one intelligent object is addressed by MAB algorithms. In that work, low-cost algorithms following two well-known approaches, such as the Upper-Confidence Bound () [2], and the Thompson Sampling (TS) algorithms [16] have reported good results. Other recent directions include theoretical analysis of application of MAB algorithms for slotted wireless protocols in a decentralized manner, see [5] and references therein, but in this work we focus on a more programmatic approach.
The aim of this paper is to assess the performance of MAB algorithms [9], used for frequency selection in IoT networks. In particular, and compared to the literature, we focus on the impact of the retransmissions on the performance of learning algorithms. Indeed, in the case where learning algorithms are used for frequency selection, IoT devices tend to focus on a single channel, which increases the probability of having several successive collisions. The contributions of this paper can be summarized as follows:
-
We first propose a closed form approximation for the probability of having a second collision after a collision has occurred in one channel,
-
Then, we introduce several heuristics so as to cope with retransmissions,
-
We finally conduct simulations in order to compare the performance of the proposed heuristics with the naive uniform random approach and the simple UCB strategy (non aware of retransmissions).
Finally, our proposal is applied in a decentralized manner, and with a low complexity that do not require any modification on network side, and it could be applied with a very low extra cost in real embedded hardware. Implementation of the model and our proposals on real hardware [18] is left as a future work.
The rest of the paper is organized as follows: first the system model is introduced in Section II. Section IV describes more formally the MAB learning algorithms. Our contributions mainly consist in heuristics, presented in Section V, while numerical results are presented in Section VI. Conclusions are given in Section VII.
Ii System model
We suppose an IoT network made of one gateway (i.e., base station), and of a large number of end-devices that regularly send short data packets to the gateway. The base station listens to a fixed set of channels (), in which devices can transmit their packets. As in [8], we suppose that the network is made of two types of devices:
-
We have a set of static end-devices. These devices are low-cost devices and are only able to use one channels. They use the same gateway as others. However, as we consider an IoT standard which operates in unlicensed bands, it could be considered that they communicate with another gateway or are using another standard, without changing much the model and our conclusion.
-
We also have dynamic devices which have the possibility to use all the available channels.
The IoT network considered here is a slotted ALOHA protocol [1], where each device has a probability to transmit a packet in a slot (first transmission). In case of collision, a device retransmits this packet after a random waiting time, uniformly distributed in , where is the length of the back-off interval. We denote by the maximum number of transmissions for each packet. We assume that, in the case where more than two devices are transmitting a packet in the same slot, all the packets are lost and must be retransmitted.
With such assumptions, we can model the behavior of end-devices using the Markov chain [14] of Figure 1.
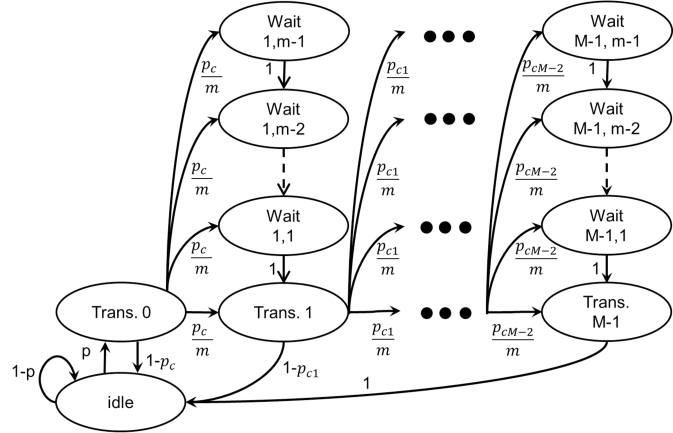
We consider orthogonal radio channels (also called arms) of different characteristics, being unknown to the device. The radio protocol is slotted in both time and frequency, meaning that at each time step , the device, tries to communicate in a channel . In our model, the device chooses one channel at a time, and use it to communicate, and waits for the gateway to send back an acknowledgement (Ack).
In the stochastic model considered in this paper, after choosing the arm ,
receiving an acknowledgement provides a reward , randomly drawn from a certain distribution depending on the arm index.
Rewards are assumed to be bounded in , and generally they follow one-parameter exponential families (a well-known example being any family of Gaussian distributions with a fixed variance).
We present our algorithm by restricting to Bernoulli distributions
Iii Motivations for the proposed approach
We can justify why the proposed approach is interesting.
Iii-a Analytic derivation
When MAB learning algorithms are used for the purpose of channel selection in an IoT network, the devices that implement them are learning to make most of their transmissions in only one channel. See for instance the numerical results presented in [7], or [17] for a different application example. However, in the case with many devices following the behavior described by Figure 1, if they are using the same channel, the probability to have a collision at the second transmission could be much higher than , the probability of having a collision at the first transmission.
The aim of this section is to propose an approximation for as a function of in order to assess the difference between these probabilities. To do so, we suppose that a device had a collision after transmitting a packet for the first time (transmission ) and we compute the probability to have a collision at the second transmission (transmission ).
Hypotheses We make two realistic hypotheses.
-
The probability to have a collision at the second transmission, , can be decomposed into the probability of having a collision with a packet transmitted by devices involved in the collision at the first transmission, which is denoted , and the probability of having a collision with a packet transmitted by other devices, not involved in the previous collision. The number of devices involved in the previous collision is supposed to be small enough, compared to the number of devices in the channel, to consider that this second probability is equal to .
-
is supposed to be large enough to consider that devices are hardly ever in this state. With this hypothesis, if a device is involved in the previous collision it retransmits its packet after a random back-off time.
We assume a steady state for the Markov chain of Figure 1 [14]. Let us consider one device in the channel. We denote the probability that it is transmitting a packet for the time in a given slot (for ), and the probability that it is transmitting in a given slot. The probability that this device has a collision at the first transmission is denoted and satisfies
| (1) |
Moreover, the probability that it has a collision with packets sent by different devices (), at the first transmission, is equal to
| (2) |
After a collision at the first transmission, the device retransmits its packet after a random back-off interval. Using hypothesis , the probability that it has a collision at the second transmission is
| (3) |
So, we need to express , the probability to have a collision with a packet involved in the previous collision, as a function of . Assuming hypothesis , is the probability that a device involved in the previous collision choose the same back-off interval. Thus is
| (4) |
where is the probability that, knowing that the device had a collision at transmission , it had a collision with packets, and that at least one of the devices involved in the previous collision choose the same back-off interval. And thus
| (5) |
We now use once again, assuming that the number of devices involved in the first collision is small compared to , the first terms of the sum of equation (5) are predominant. Moreover, for these terms, is small compared to , so . So,
| (6) |
We can use the binomial theorem to compute the sum in (III-A), and we obtain the expression of
| (7) |
Iii-B Numerical validation
In order to assess the proposed approximation, we suppose a channel in which all the devices have the same behavior. In this single channel, the ALOHA protocol is using a maximum number of transmissions of each message of , a back-off interval of maximum length , and a probability of transmission of . Figure 2 shows the probability of collision in the channel, versus the number of devices.
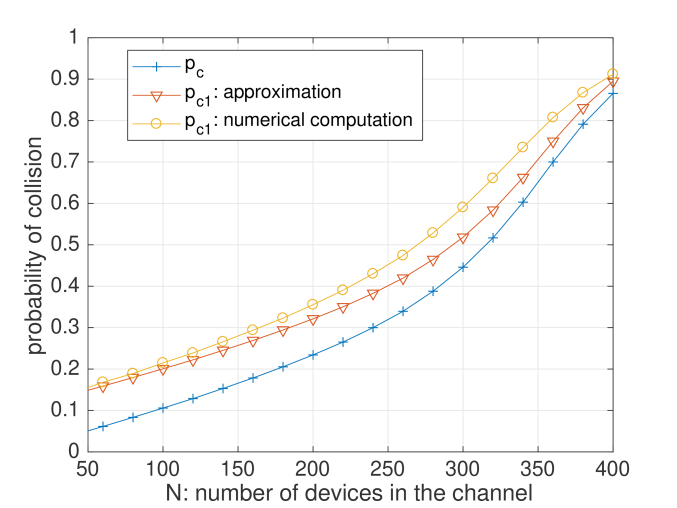
We can see in Figure 2 that the proposed approximation is precise where , i.e., where the gap between and is the higher. Moreover, we can see in this figure that the gap between and can be of up to , which emphasizes the possible interest of improving MAB algorithms, so that they do not use the same channel for retransmissions.
Iv A well-known MAB Algorithm:
Before presenting different ways to incorporate the retransmissions, we present a classical bandit algorithm as a base building block. We chose to restrict to the algorithm [3], which is known to be efficient for stationary i.i.d. rewards while being simple to present, and being simple enough to be implemented in practice for embedded hardware. In this section, let us consider one device, which tries to learn how to reduce its PLR while accessing the network, without taking into account the retransmission aspect of our model. More details on this simpler variant can be found in previous work [7] and more theoretical details are given, e.g., in [9, 5].
Iv-a Smart devices cannot be greedy
A first approach is to use an empirical mean estimator of the rewards in every channel, and select the channel with highest estimated mean at every time step; but this greedy approach is known to fail dramatically [13]. Indeed, with this policy, the selection of arms depends too much on the first draws: if the first transmission in one channel fails and the first one on other channels succeed, the device will never use the first channel again, even it is the best one (i.e., the most available, in average).
Iv-B The algorithm
Rather than relying on the empirical mean reward, Upper Confidence Bounds algorithms instead use a confidence interval on the unknown mean of each arm, which can be viewed as adding a “bonus” exploration to the empirical mean. They follow the “optimism-in-face-of-uncertainty” principle: at each step, they play according to the best model, as the statistically best possible arm (i.e., the highest UCB) is selected.
More formally, for one device, let be the number of times channel was selected up-to time ,
| (8) |
The empirical mean estimator of channel is defined as the mean reward obtained by selecting it up to time ,
| (9) |
For , the confidence term is given by [3]
| (10) |
giving the upper confidence bound , which is used by the device to decide the channel for communicating at time step : . is called an index policy.
The algorithm uses a parameter , originally was set to [2], but empirically is known to work better (uniformly across problems), even though was advised by the theory [9]. In our model, every dynamic device implements its own algorithm, independently. For one device, the time is the total number of sent messages from the beginning, as rewards are only obtained after a transmission. Algorithm 1 presents the pseudo-code of . Note that no matter if it is the first transmission or a retransmission of a message, this first proposal uses the same access scheme and updates the internal data in a similar way.
V Proposed Heuristics
Machine learning algorithms, and especially the MAB framework, has been used in simpler cognitive radio models before, starting from [12] and more recently in [7, 8], for instance. The novelty of our approach relies on the proposed heuristics that try to take into account the retransmission aspect of our model.
In our model, any dynamic object knows when it is retransmitting or sending for the first time, but using the unmodified algorithm for decision making (i.e., channel selection) in both cases do not use this information. As usual in reinforcement learning, a natural question is to evaluate whether using this additional contextual information can improve the performance of the learning policy.
We present in this Section some heuristics, that use this information in various ways. They vary only in their way to select channels for retransmissions, and all retransmissions are dealt with similarly (no distinction is done between the first retransmission and the next ones). All the following algorithms follow the same pattern as Algorithm 1.
V-a then uniform random access
This first proposal is a simple mixture between the approach presented in Section IV-B and the naive Random Uniform Access approach, see Algorithm 2 below. It uses a to select channels for the first transmission of each message, and in case of any retransmission, it uses a random channel selection. The idea is to learn to use the best channel for first transmission, then avoid using the best channel too much for the retransmissions. It is the simplest heuristic, inspired from the observations on being larger than presented in Section III-B.
V-B Two
Another heuristic is presented in Algorithm 3: it tries to learn more, and it uses two different learning algorithms. As for all heuristics, one algorithm is used to select the channels for the first transmissions, but now the channels for retransmissions are not randomly selected but are selected using a second
V-C One then
Extending the idea of the previous heuristics, we also propose a similar one, which uses algorithms instead of simply two, see Algorithm 4.
One is again used for selecting channels for the first transmissions, and now different and independent algorithms
V-D Two with delay for the second one
The last heuristic we propose is a mixture of Algorithms 2 and 3, see Algorithm 5.
Fix a delay , e.g., steps
Vi Experiment Results
We simulate our network in order to compare the proposed heuristics. The simulated network uses similar values of the ALOHA model as the one used for Figure 2: , , and . We consider channels (like for the LoRa standard), a number of time slots , which is large enough to observe convergence of all learning algorithms. Moreover the results are averaged on independent runs of the random simulation. We consider a total number of devices of , and a non-uniform repartition of static devices of in the channels.
We present in Figure 3 the results of this numerical simulation. The axis corresponds to the number of communications of a device, and it corresponds to the number of learning step, while the axis corresponds to the successful transmission rate, in percentage.
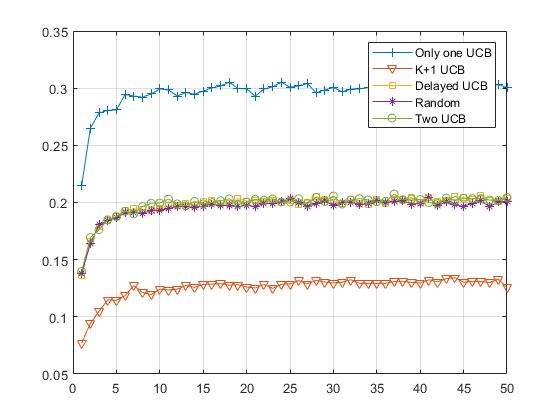
We verify that each proposal is indeed learning, as its successful transmission rate is rapidly increasing (or equivalently, its PLR is decreasing). All plots show a pattern typical of MAB algorithms when applied to this kind of problem: a fast learning phase in the beginning of the experiment and a “plateau” showing the convergence of the algorithm to a stable strategy.
All heuristics outperform the naive random uniform approach, which is not included to reduce clutter in the plot. The random approach has a successful transmission rate of about , constant in time as no learning is involved, and for instance the best heuristic attains a performance up-to times better, at about . Observing such a strong improvement in terms of successful transmission rate is a very strong advocate of using simple MAB learning algorithm.
The conclusions we can draw from this simulation are twofold. First of all, a simple sanity check is that all the proposed heuristics do not reduce performance when compared to the naive approach. But most importantly, we observe three groups of heuristics. The less efficient one is the , and this makes sense as having more learning algorithm needs more for each of them to learn. The more efficient one is the simple procedure, and this was quite surprising. All the other heuristics perform very much similarly.
Vii Conclusion
Summary
In this paper, we presented a model of IoT networks based on a ALOHA protocol, slotted both in time and frequency, in which dynamic objects can use machine learning algorithms to improve their Packet Loss Ratio when accessing the network. The main novelty of this model is that it allows device to retransmit a packet in case of collision, and by using the framework of Multi-Armed Bandit, we presented and evaluated several learning heuristics that try to learn how to transmit and retransmit in a smarter way. Empirical simulations show that each heuristics outperform the naive uniform access scheme, and we conclude that the simple learning approach is the most efficient.
Future works
Possible extensions include studying other families of algorithms, such at Thompson Sampling [16], or non-stochastic MAB algorithms such as the Exp family [9]. We also want to study more heuristics, and one interesting idea is to consider variants of stochastic MAB algorithms such as Sliding Window UCB or Discounted UCB [10], or smarter and more recent algorithms. As they are tailored to be robust to non-stationary MAB problems with small dynamic behaviors, applying our heuristics to such base algorithm could help to be more adaptive to the intrinsic non-stationarity of the network.
Simulation code
The source code (MATLAB or Octave) used for the simulations and the figures is open-sourced under the MIT License, at Bitbucket.org/scee_ietr/ucb_smart_retrans.
Footnotes
- thanks: This work is supported by the French National Research Agency (ANR), under the projects SOGREEN and EPHYL (grants coded: N Anr-14-Ce28-0025-02 and N. Anr-16-Ce25-0002-03), by Région Bretagne, France, the French Ministry of Higher Education and Research (MENESR), and École Normale Supérieure de Paris-Saclay.
- The model is similar for other distributions, and we also tested our proposal with Gaussian distributions, with finite support in , and similar conclusions were observed. Non-discrete rewards are interpreted as a relative communication efficiency, instead of binary available/busy information, but we do not cover this aspect in more details in this work.
- The storage requirements and time complexity is doubled but remains linear w.r.t. , and so it is still a practical proposal.
- The storage requirements and time complexity is now quadratic in , and as such we no longer consider this heuristic to be a practical proposal in some IoT networks, as for instance Sigfox networks consist in a large number of very narrow-band channels. But for LoRaWAN networks with , storing algorithms does not cost much more than storing .
- Choosing the value of could be done by extensive benchmarks but such approach goes against the reinforcement learning idea: an heuristic should work against any problem, without the need to be able to simulate the problem in advance in order to find a good value of some internal parameter. As such, we only consider a delay of .
- Cf. the page www-scee.rennes.supelec.fr/wp/testbed/ and the associated publications, it is also presented in details in [6].
References
- (1970) The ALOHA System: Another Alternative for Computer Communications. In Proceedings of the November 17-19, 1970, Fall Joint Computer Conference, AFIPS ’70 (Fall), New York, NY, USA, pp. 281–285. External Links: Link, Document Cited by: §II.
- (2002) Finite-time Analysis of the Multi-armed Bandit Problem. Machine Learning 47 (2), pp. 235–256. External Links: Document, ISSN 1573-0565 Cited by: §I, §IV-B.
- (2002) The Non-Stochastic Multi-Armed Bandit Problem. SIAM Journal on Computing 32 (1), pp. 48–77. Cited by: §IV-B, §IV.
- (2018-12) Self-organized Low-power IoT Networks: A Distributed Learning Approach. In IEEE Globecom 2018, Cited by: §I.
- (2018) Multi-Player Bandits Revisited. In Algorithmic Learning Theory, Lanzarote, Spain. External Links: Link Cited by: §I, §IV.
- (2017) Coexistence of Communication Systems Based on Enhanced Multi-Carrier Waveforms with Legacy OFDM Networks. Ph.D. Thesis, CentraleSupélec. External Links: Link Cited by: footnote 5.
- (2017) Multi-Armed Bandit Learning in IoT Networks: Learning helps even in non-stationary settings. In 12th EAI Conference on Cognitive Radio Oriented Wireless Network and Communication, CROWNCOM Proceedings. Cited by: §I, §III-A, §IV, §V.
- (2018) Improvement of the LPWAN AMI backhaul’s latency thanks to reinforcement learning algorithms. EURASIP Journal on Wireless Communications and Networking 2018 (1), pp. 34. External Links: ISSN 1687-1499, Document Cited by: §I, §II, §V.
- (2012) Regret analysis of stochastic and nonstochastic multi-armed bandit problems. Foundations and Trends® in Machine Learning 5 (1), pp. 1–122. Cited by: §I, §I, §IV-B, §IV, §VII.
- (2008) On Upper-Confidence Bound Policies For Non Stationary Bandit Problems. arXiv preprint arXiv:0805.3415. Cited by: §VII.
- GNU Radio Documentation. Note: https://www.gnuradio.org/about/ Accessed: 2018-09-25 Cited by: §VII.
- (2010) Upper Confidence Bound based decision making strategies and Dynamic Spectrum Access. In IEEE International Conference on Communications (ICC), pp. 1–5. Cited by: §V.
- (1985) Asymptotically efficient adaptive allocation rules. Advances in Applied Mathematics 6 (1), pp. 4–22. Cited by: §IV-A.
- (1998) Markov Chains. Cambridge Series in Statistical and Probabilistic Mathematics, Vol. 2, Cambridge University Press, Cambridge. Cited by: Fig. 1, §II, §III-A.
- (2017-Secondquarter) Low power wide area networks: an overview. IEEE Communications Surveys Tutorials 19 (2), pp. 855–873. External Links: Document, ISSN Cited by: §I.
- (1933) On the likelihood that one unknown probability exceeds another in view of the evidence of two samples. Biometrika 25 (3/4), pp. 285–294. Cited by: §I, §VII.
- (2016) A Thompson Sampling approach to channel exploration-exploitation problem in multihop cognitive radio networks. In PIMRC, pp. 1–6. External Links: Document Cited by: §III-A.
- USRP Hardware Driver and USRP Manual. Note: http://files.ettus.com/manual/page_usrp2.html Accessed: 2018-09-25 Cited by: §I, §VII.