(*
This OCaml script was exported from a Jupyter notebook
using an open-source software (under the MIT License) written by @Naereen
from https://github.com/Naereen/Jupyter-Notebook-OCaml
This software is still in development, please notify me of a bug at
https://github.com/Naereen/Jupyter-Notebook-OCaml/issues/new if you find one
*)
(* # Table of Contents
*)
(* # Texte d'oral de modélisation - Agrégation Option Informatique *)
(* ## Préparation à l'agrégation - ENS de Rennes, 2016-17 *)
(* - *Date* : 29 mai 2017
- *Auteur* : [Lilian Besson](https://GitHub.com/Naereen/notebooks/)
- *Texte*: [Taquin (pub2008-D2)](http://agreg.org/Textes/pub2008-D2.pdf) *)
(* ## À propos de ce document *)
(* - Ceci est une *proposition* de correction, partielle et probablement non-optimale, pour la partie implémentation d'un [texte d'annale de l'agrégation de mathématiques, option informatique](http://Agreg.org/Textes/).
- Ce document est un [notebook Jupyter](https://www.Jupyter.org/), et [est open-source sous Licence MIT sur GitHub](https://github.com/Naereen/notebooks/tree/master/agreg/), comme les autres solutions de textes de modélisation que [j](https://GitHub.com/Naereen)'ai écrite cette année.
- L'implémentation sera faite en OCaml, version 4+ : *)
(* In[1]: *)
Sys.command "ocaml -version";;
(* > Notez que certaines fonctions des modules usuels [`List`](http://caml.inria.fr/pub/docs/manual-ocaml/libref/List.html) et [`Array`](http://caml.inria.fr/pub/docs/manual-ocaml/libref/List.html) ne sont pas disponibles en OCaml 3.12.
> J'essaie autant que possible de ne pas les utiliser, ou alors de les redéfinir si je m'en sers. *)
(* ---- *)
(* ## Question de programmation *)
(* La question de programmation pour ce texte était donnée en page 5, et était assez courte :
> "Implanter l'algorithme qui, à partir d'une table $T$ du jeu de taquin, calcule les coordonnées du trou et la valeur de $\pi_2(T)$." *)
(* ---- *)
(* ## Réponse à l'exercice requis *)
(* ### Structures de données
On doit pouvoir représenter $T$, une table du jeu de taquin.
On utilisera la structure de données suggérée par l'énoncé :
> "Une table $T$ du jeu de taquin est codée par un tableau carré (encore noté $T$) où, pour $i, j \in [| 0, n - 1 |]$, $T[i, j]$ désigne le numéro de la pièce située en ligne $i$ et colonne $j$, le trou étant codé par l’entier $0$."
La figure 1 présente trois tables du jeu pour $n=4$; la première, notée $T_1$ , est aléatoire, la troisième est la table finale $T_f$ et la deuxième, notée $T_2$, peut être qualifiée d’intermédiaire : il est possible de passer en un certain nombre de coups de $T_1$ à $T_2$, puis de $T_2$ à $T_f$.
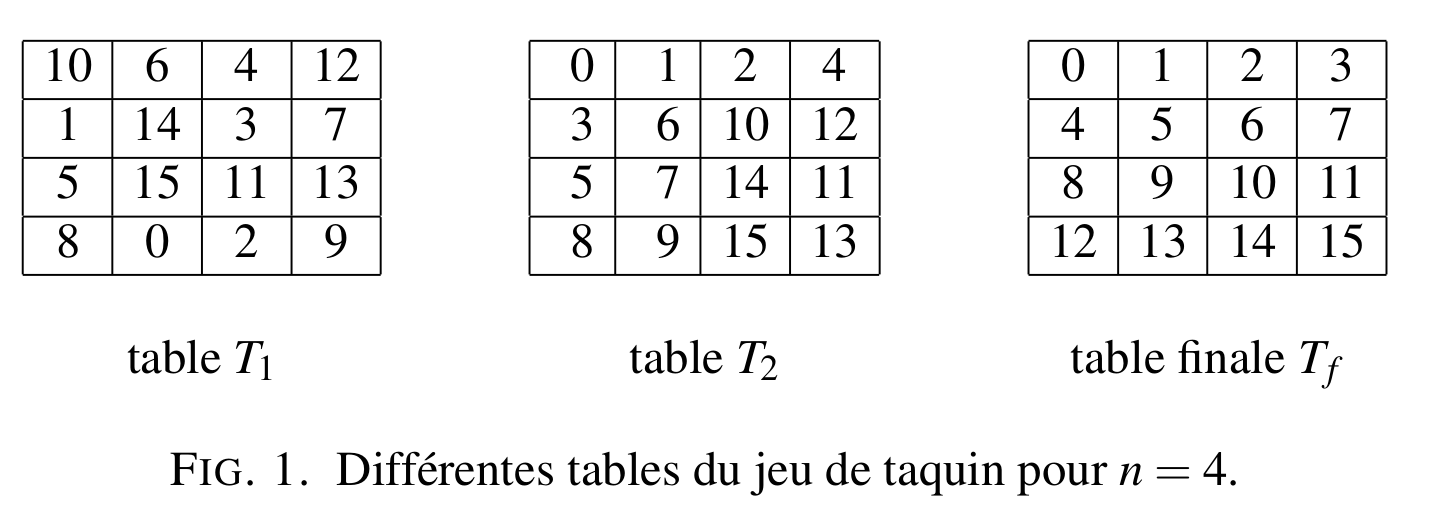
Par exemple, dans la table $T_1$ de la figure $1$, $T_1[2, 0] = 5$ et le trou est situé à la position $[3, 1]$. *)
(* In[2]: *)
type taquin = int array array;;
(* ### Exemples de grilles
On reproduit les trois exemples ci-dessous : *)
(* In[3]: *)
let t1 : taquin = [|
[| 10; 6; 4; 12 |];
[| 1; 14; 3; 7 |];
[| 5; 15; 11; 13 |];
[| 8; 0; 2; 9 |]
|];;
(* In[4]: *)
let t2 : taquin = [|
[| 0; 1; 2; 4 |];
[| 3; 6; 10; 12 |];
[| 5; 7; 14; 11 |];
[| 8; 9; 15; 13 |]
|];;
(* In[5]: *)
let tf : taquin = [|
[| 0; 1; 2; 3 |];
[| 4; 5; 6; 7 |];
[| 8; 9; 10; 11 |];
[| 12; 13; 14; 15 |]
|];;
(* ### Permutations
On peut essayer d'obtenir les deux permutations, $\sigma(T)$ et $\sigma^B(T)$, pour une table $T$ donnée.
Une permutation sera un simple tableau, de tailles $n^2$ (pour $\sigma$) et $n^2 - 1$ (pour $\sigma^B$), qui stocke en case $i$ la valeur $\sigma(T)[i]$. *)
(* In[6]: *)
type permutation = int array ;;
(* In[7]: *)
let sigma (t : taquin) : permutation =
(* Initialisation *)
let n = Array.length t in
let sigm = Array.make (n * n) 0 in
(* Remplissons sigm *)
for i = 0 to n - 1 do
for j = 0 to n - 1 do
sigm.( i * n + j ) <- t.(i).(j)
done;
done;
sigm
(* On aurait aussi pu faire
Array.init (n * n) (fun ij -> t.(ij mod n).(j / n))
*)
;;
(* Exemples : *)
(* In[8]: *)
sigma t1;;
sigma t2;;
sigma tf;;
(* C'était facile.
Maintenant pour la permutation de Boustrophédon, $\sigma^B(T)$.
On va quand même stoquer le $0$, en position $0$. *)
(* In[9]: *)
let print = Printf.printf;;
(* In[10]: *)
let sigmaB (t : taquin) : permutation =
(* Initialisation *)
let n = Array.length t in
let sigm = Array.make ((n * n) - 1) 0 in
let nbzero = ref 0 in
(* Remplissons sigm *)
for i = 0 to n - 1 do
for j = 0 to n - 1 do
if i mod 2 = 0
then (* gauche à droite *)
if t.(i).(j) = 0 then
incr nbzero
else
sigm.( i * n + j - !nbzero ) <- t.(i).(j)
else (* droite à gauche *)
if t.(i).(n - j - 1) = 0 then
incr nbzero
else
sigm.( i * n + j - !nbzero ) <- t.(i).(n - j - 1)
done;
done;
sigm
;;
(* Exemples : *)
(* In[11]: *)
sigmaB t1;;
sigmaB t2;;
sigmaB tf;;
(* ### Un déplacement
On a $4$ déplacements possibles, $\{N, E, S, O\}$. *)
(* In[12]: *)
type deplacement = Nord | Est | Sud | Ouest ;;
(* On va avoir besoin d'une fonction qui trouve la position $(i,j)$ du trou : *)
(* In[13]: *)
let ou_est (x : int) (t : taquin) : (int * int) =
let n = Array.length t in
let ij = ref (0, 0) in
for i = 0 to n - 1 do
for j = 0 to n - 1 do
if t.(i).(j) = x then
ij := (i, j)
done;
done;
!ij
;;
let ou_est_trou = ou_est 0 ;;
(* In[14]: *)
let copie (t : taquin) : taquin =
Array.map (Array.copy) t
;;
(* In[15]: *)
let unmouvement (t : taquin) (dir : deplacement) : taquin =
let n = Array.length t in
let i, j = ou_est_trou t in
let tsuivant = copie t in
match dir with
| Nord ->
if i = 0
then
failwith "Can't go north here"
else begin
tsuivant.(i).(j) <- tsuivant.(i - 1).(j);
tsuivant.(i - 1).(j) <- 0;
tsuivant
end;
| Est ->
if j = n - 1
then failwith "Can't go east here"
else begin
tsuivant.(i).(j) <- tsuivant.(i).(j + 1);
tsuivant.(i).(j + 1) <- 0;
tsuivant
end;
| Sud ->
if i = n - 1
then failwith "Can't go south here"
else begin
tsuivant.(i).(j) <- tsuivant.(i + 1).(j);
tsuivant.(i + 1).(j) <- 0;
tsuivant
end;
| Ouest ->
if j = 0
then failwith "Can't go west here"
else begin
tsuivant.(i).(j) <- tsuivant.(i).(j - 1);
tsuivant.(i).(j - 1) <- 0;
tsuivant
end;
;;
(* In[16]: *)
let t1' = unmouvement t1 Nord ;;
sigma t1';;
(* Ça semble fonctionner comme dans l'exemple du texte. *)
(* ### Test de la parité de $\sigma^B$
Le critère suivant permet de savoir si une table de taquin est jouable, i.e, si on peut la résoudre :
> $T$ est jouable si et seulement si $\sigma^B(T)$ est paire. *)
(* In[17]: *)
let nb_inversions (sigm : permutation) : int =
let nb = ref 0 in
let m = Array.length sigm in
for i = 0 to m - 1 do
for j = i + 1 to m - 1 do
if sigm.(i) > sigm.(j) then
incr nb
done;
done;
!nb
;;
(* In[18]: *)
let est_paire (sigm : permutation) : bool =
((nb_inversions sigm) mod 2) = 0
;;
(* On peut vérifier que les trois tables de l'énoncé ont bien une permutation de Boustrophédon paire : *)
(* In[19]: *)
est_paire (sigmaB t1);;
est_paire (sigmaB t2);;
est_paire (sigmaB tf);;
(* Et l'exemple de l'énonce qui n'est plus *jouable* : *)
(* In[20]: *)
let tnof = copie tf in
tnof.(0).(1) <- 2;
tnof.(0).(2) <- 1;
est_paire (sigmaB tnof);;
(* In[21]: *)
let est_jouable (t : taquin) : bool =
est_paire (sigmaB t)
;;
(* ### Fonctions demandées
- On a déjà écrit la fonction $\pi_1(T)$, `nb_inversions`.
- Pour $\pi_2(T)$, on doit réfléchir un peu plus. *)
(* In[22]: *)
let pi_1 (t : taquin) : int =
nb_inversions (sigma t)
;;
(* Pour $\pi_2(T)$, on peut être inquiet de voir dans la définition de cette distance la table finale, qui est l'objectif de la résolution du problème, mais en fait les tables finales $T_f$ ont toutes la même forme : en case $(i,j)$ se trouve $i \times n + j$ ! *)
(* On commence par définir la norme $\ell_1$, sur deux couples $(i,j)$ et $(x,y)$ :
$$ \ell_1 : (i,j), (x, y) \mapsto |i-x| + |j-y| $$ *)
(* In[23]: *)
let norme_1 (ij : int * int) (xy : int * int) : int =
let i, j = ij and x, y = xy in
abs(i - x) + abs(j - y)
;;
(* Puis la distance définie $d(T[i,j])$ dans l'énoncé : *)
(* In[24]: *)
let distance (t : taquin) (i : int) (j : int) : int =
let n = Array.length t in
let valeur = t.(i).(j) in
let ifin, jfin = valeur / n, valeur mod n in
norme_1 (i, j) (ifin, jfin)
;;
(* Et enfin la fonction $\pi_2(T)$ est facile à obtenir : *)
(* In[25]: *)
let pi_2 (t : taquin) : int =
let n = Array.length t in
let d = ref 0 in
for i = 0 to n - 1 do
for j = 0 to n - 1 do
if t.(i).(j) != 0
then
d := !d + (distance t i j)
done;
done;
!d
;;
(* ### Exemples
On prend l'exemple du texte avec $T_1$.
- $d(T_1[0,3]) = 6$ ? *)
(* In[26]: *)
distance t1 0 3;;
(* - $\pi_2(T) = 38$ ? *)
(* In[27]: *)
pi_2 t1;;
(* Ça semble bon ! *)
(* Avec $T_2$ : *)
(* In[28]: *)
distance t2 0 3;;
(* In[29]: *)
pi_2 t2;;
(* Avec $T_f$, évidemment $\pi_2(T) = 0$ puisque $T_f$ est résolue : *)
(* In[30]: *)
distance tf 0 3;;
(* In[31]: *)
pi_2 tf;;
(* ----
## Bonus ? *)
(* ### Complexité
- La fonction $\pi_1(T)$ est en $\mathcal{O}(N)$ en temps et mémoire, si $N = n^2$ est le nombre d'éléments dans le tableau.
- La fonction $\pi_2(T)$ est aussi en $\mathcal{O}(N)$ en temps et mémoire, si $N = n^2$ est le nombre d'éléments dans le tableau. *)
(* ### Autres idées
- On pourrait faire deux versions améliorées des fonctions $\pi_1$ et $\pi_2$ pour calculer $\pi(s_a(T))$ efficacement en fonction de $\pi(t)$ et $a \in \{N, E, S, O\}$. Sans écrire le code, elles seraient en temps constant, puisqu'il faut enlever et rajouter une (ou deux) valeurs dans une somme. *)
(* - On pourrait implémenter l'algorithme "ligne à ligne". *)
(* - On pourrait implémenter d'autres algorithmes de résolution, et les vérifier sur un exemple non trivial. *)
(* ----
## Conclusion *)
(* Voilà pour les deux questions obligatoires de programmation :
- on a décomposé le problème en sous-fonctions,
- on a essayé d'être fainéant, en réutilisant les sous-fonctions,
- on a fait des exemples et *on les garde* dans ce qu'on présente au jury,
- on a testé la fonction exigée sur un exemple venant du texte,
- et on a essayé d'en faire un peu plus (au début).
> Bien-sûr, ce petit notebook ne se prétend pas être une solution optimale, ni exhaustive. *)