(*
This OCaml script was exported from a Jupyter notebook
using an open-source software (under the MIT License) written by @Naereen
from https://github.com/Naereen/Jupyter-Notebook-OCaml
This software is still in development, please notify me of a bug at
https://github.com/Naereen/Jupyter-Notebook-OCaml/issues/new if you find one
*)
(* # Table of Contents
*)
(* # Texte d'oral de modélisation - Agrégation Option Informatique
## Préparation à l'agrégation - ENS de Rennes, 2016-17
- *Date* : 7 avril 2017
- *Auteur* : [Lilian Besson](https://GitHub.com/Naereen/notebooks/)
- *Texte*: Annale 2009, "Contraintes temporelles" *)
(* ## À propos de ce document
- Ceci est une *proposition* de correction, partielle et probablement non-optimale, pour la partie implémentation d'un [texte d'annale de l'agrégation de mathématiques, option informatique](http://Agreg.org/Textes/).
- Ce document est un [notebook Jupyter](https://www.Jupyter.org/), et [est open-source sous Licence MIT sur GitHub](https://github.com/Naereen/notebooks/tree/master/agreg/), comme les autres solutions de textes de modélisation que [j](https://GitHub.com/Naereen)'ai écrite cette année.
- L'implémentation sera faite en OCaml, version 4+ : *)
(* In[2]: *)
Sys.command "ocaml -version";;
(* > Notez que certaines fonctions des modules usuels [`List`](http://caml.inria.fr/pub/docs/manual-ocaml/libref/List.html) et [`Array`](http://caml.inria.fr/pub/docs/manual-ocaml/libref/List.html) ne sont pas disponibles en OCaml 3.12.
> J'essaie autant que possible de ne pas les utiliser, ou alors de les redéfinir si je m'en sers. *)
(* ----
## Question de programmation
La question de programmation pour ce texte était donnée en question 1 en page 9 :
> "Programmer l'algorithme PC. Faites le tourner sur l'exemple de réseau non distributif."
La consigne était très courte, mais avec aucune indication.
Notez qu'il est rare que le texte exige un exemple particulier. *)
(* ----
## Réponse à l'exercice requis
Ça va être assez long, en fait...
1. D'abord, il faut définir les types de données avec lesquels on va travailler,
2. Ensuite, implémenter les deux opérations $\oplus$ et $\otimes$ sur les ensembles d'intervalles,
3. Puis implémenter l'algorithme PC (similaire à Floyd-Warshall),
4. Et enfin, l'exécuter sur l'exemple de réseau non distributif donné en page 8.
Si possible, on va essayer de faire des *tests* pour chaque fonction intermédiaire, et un exemple de plus à la fin.
Un des problèmes que l'on va rencontrer est le fait que l'on doit manipuler $-\infty$ et $+\infty$, pour pouvoir gérer une contrainte qui n'est pas une contrainte, à savoir l'interavalle $(-\infty, +\infty)$. *)
(* ----
### Structures de données
On va travailler avec des valeurs entières ou $\pm\infty$. En écrivant nous même les opérations arithmétiques ($+,max$) sur les entiers "étendus" on obtiendra ce qu'on veut. *)
(* In[75]: *)
type entier_etendu = MInf | PInf | E of int;;
(* On se restreint aux intervalles à coordonnées *entières*, et on considère des listes d'intervalles.
Tous les intervalles sont fermés à gauche et à droite. *)
(* In[76]: *)
type intervalle = (entier_etendu * entier_etendu);; (* (a, b) représente l'intervalle [a, b] *);;
(* In[77]: *)
type intervalles = intervalle list;;
(* On définit tout de suite deux exemples, $T_a$ et $S_a$ tirés de la Figure 2.a) et $T_b,S_b$ de la Figure 2.b).
Cela permettra de vérifier les opérations $\oplus$ et $\otimes$. *)
(* - $T_a = \{ [1, 4], [6, 8] \}$ et $S_a = \{ [0, 1], [3, 5], [6, 7] \}$. *)
(* In[78]: *)
let t_a : intervalles = [
(E(1), E(4));
(E(6), E(8))
];;
let s_a : intervalles = [
(E(0), E(1));
(E(3), E(5));
(E(6), E(7))
];;
(* - $T_b = \{ [-1, 0], [2, 4] \}$ et $S_b = \{ [0, 1], [4, 4] \}$. *)
(* In[80]: *)
let t_b : intervalles = [
(E(-1), E(0));
(E(2), E(4))
];;
let s_b : intervalles = [
(E(0), E(1));
(E(4), E(4)) (* Intervalle de longueur nulle *)
];;
(* - Et la contrainte vide, $T = \{[-\infty, +\infty\}$ : *)
(* In[79]: *)
let t_vide : intervalles = [
(MInf, PInf)
];;
(* ---
### Arithmétiques sur nos entiers étendus *)
(* #### Max/min *)
(* In[81]: *)
let max_ee x y =
match x, y with
| MInf, _ -> y
| PInf, _ -> PInf
| _, MInf -> x
| _, PInf -> PInf
| E(vx), E(vy) -> E(max vx vy)
;;
(* In[86]: *)
max_ee MInf (E(10));;
max_ee PInf (E(10));;
max_ee (E(10)) MInf;;
max_ee (E(10)) PInf;;
max_ee (E(-10)) (E(10));;
max_ee (E(10)) (E(-10));;
(* In[87]: *)
let min_ee x y =
match x, y with
| PInf, _ -> y
| MInf, _ -> MInf
| _, PInf -> x
| _, MInf -> MInf
| E(vx), E(vy) -> E(min vx vy)
;;
(* In[90]: *)
min_ee MInf (E(10));;
min_ee PInf (E(10));;
min_ee (E(10)) MInf;;
min_ee (E(10)) PInf;;
min_ee (E(-10)) (E(10));;
min_ee (E(10)) (E(-10));;
(* On peut utiliser la fonction minimum pour trier deux entiers étendus : *)
(* In[115]: *)
let pluspetiteq_ee x y =
let m = min_ee x y in
m = x || x = y
;;
(* In[116]: *)
let pluspetit_ee x y =
let m = min_ee x y in
m = x && x != y
;;
(* #### Somme/produit *)
(* In[88]: *)
let plus_ee x y =
match x, y with
| MInf, PInf -> failwith "-inf + +inf = ?"
| PInf, MInf -> failwith "-inf + +inf = ?"
| PInf, _ -> PInf
| MInf, _ -> MInf
| _, MInf -> MInf
| _, PInf -> PInf
| E(vx), E(vy) -> E(vx + vy)
;;
(* In[92]: *)
plus_ee MInf (E(10));;
plus_ee PInf (E(10));;
plus_ee (E(10)) MInf;;
plus_ee (E(10)) PInf;;
plus_ee (E(-10)) (E(10));;
plus_ee (E(10)) (E(-10));;
plus_ee (E(10)) (E(10));;
plus_ee (E(-10)) (E(-10));;
(* In[93]: *)
let produit_ee x y =
match x, y with
| MInf, PInf -> MInf
| PInf, MInf -> PInf
| PInf, E(vy) when vy < 0 -> MInf
| PInf, _ -> PInf
| MInf, E(vy) when vy < 0 -> PInf
| MInf, _ -> MInf
| E(vx), PInf when vx < 0 -> MInf
| _, PInf -> PInf
| E(vx), MInf when vx < 0 -> PInf
| _, MInf -> MInf
| E(vx), E(vy) -> E(vx * vy)
;;
(* In[94]: *)
produit_ee MInf (E(10));;
produit_ee PInf (E(10));;
produit_ee (E(10)) MInf;;
produit_ee (E(10)) PInf;;
produit_ee (E(-10)) (E(10));;
produit_ee (E(10)) (E(-10));;
produit_ee (E(10)) (E(10));;
produit_ee (E(-10)) (E(-10));;
(* ----
### Opérations de base, $\oplus$ et $\otimes$
On peut écrire des opérations d'intersection et de composition sur deux intervalles, ensuite il suffira de les généraliser à un ensemble d'intervalle.
On suit les définitions de l'énoncé.
#### Intersection
$$
\forall T = (I_1,\dots,I_l),
\forall S = (J_1,\dots,J_m),\\
T \oplus S := \{ K_1, \dots, K_n\}
\;\;\text{Où}\;\; K_k = I_i \cap J_j.
$$
Notez que $n \leq l + m$ ici. *)
(* Pour l'intersection de deux intervalles, l'intervalle vide $\emptyset$ peut être obtenu, donc la fonction suivante renvoie un type `intervalle option` : soit `None` si $I \cap J = \emptyset$, soit `Some (x, y)` si $I \cap J = [x, y]$. *)
(* In[96]: *)
let intersection (i : intervalle) (j : intervalle) : intervalle option =
let a = fst i and b = snd i in
let c = fst j and d = snd j in
if pluspetit_ee b c || pluspetit_ee d a then
None
else
Some (max_ee a c, min_ee b d)
;;
(* Ensuite, il suffit d'explorer tous les couples $(I, J)$ possible, et de ne garder que ceux qui donnent un intervalle.
On supprimera les doublons en vérifiant au fur et à mesure (ça a la même complexité que si on le fait à la fin).
En manipulant une liste d'intervalle `option`, on doit ruser un peu pour n'ajouter que ceux qui ne sont pas dans `acc` et qui sont des vrais intervalles. *)
(* In[98]: *)
let ajoute_nouveaux_option (acc : intervalles) (liste_option : intervalle option list) =
List.map
(fun i -> match i with Some i2 -> i2 | None -> (MInf, PInf))
(List.filter (fun i ->
match i with
| None -> false
| Some i2 -> not (List.mem i2 acc)
) liste_option)
;;
(* Avec tout ça, on a une belle fonction récursive, avec un accumulateur `acc` qui contient la liste des intervalles dans $T \oplus S$, construite en considérant les intervalles de $S$ les un après les autres.
On s'assure de n'avoir ni intervalles vide, ni doublon, grâce à `ajoute_nouveaux_option`. *)
(* In[101]: *)
let intersections (t : intervalles) (s : intervalles) : intervalles =
let rec inter_aux acc tx sx =
match sx with
| [] -> acc (* Plus rien à ajouter *)
| j :: s2 -> (* On traite j, puis récursivement la suite de s *)
let t_inter_j = List.map (intersection j) tx in
inter_aux ((ajoute_nouveaux_option acc t_inter_j) @ acc) tx s2
in
List.sort compare (inter_aux [] t s)
(* On trie pour les avoir en ordre croissant, c'est tout *)
;;
(* Pour frimer un peu et simplifier l'écriture de l'algorithme PC, on peut définir une opération infixe en raccourci :
$$ T \oplus S = \texttt{t ++ s}.$$ *)
(* In[102]: *)
let ( ++ ) = intersections;;
(* #### Composition
Ce sera plus facile.
$$
\forall T = (I_1,\dots,I_l),
\forall S = (J_1,\dots,J_m),\\
T \otimes S := \{ K_1, \dots, K_n\}
\;\;\text{Où}\;\; K_k = [a + c, b + d], \;\text{si}\; I_i = [a, b], J_j = [c, d].
$$
Notez que $n \leq l \times m$ ici. *)
(* Pour la composition de deux intervalles, il n'y pas de difficulté particulière : *)
(* In[103]: *)
let composition (i : intervalle) (j : intervalle) : intervalle =
let a = fst i and b = snd i in
let c = fst j and d = snd j in
(* (a + c, b + d) *)
((plus_ee a c), (plus_ee d b))
;;
(* Et on les combine facilement, en gardant la même architecture que pour `intersections`. *)
(* In[104]: *)
let ajoute_nouveaux (acc : intervalles) (liste : intervalles) : intervalles =
List.filter (fun i -> not (List.mem i acc)) liste
;;
(* In[105]: *)
let compositions (t : intervalles) (s : intervalles) : intervalles =
let rec compo_aux acc tx sx =
match sx with
| [] -> acc (* Plus rien à ajouter *)
| j :: s2 -> (* On traite j, puis récursivement la suite de s *)
let t_compo_j = List.map (composition j) tx in
compo_aux ((ajoute_nouveaux acc t_compo_j) @ acc) tx s2
in
List.sort compare (compo_aux [] t s)
(* On trie pour les avoir en ordre croissant, c'est tout *)
;;
(* Pour frimer un peu et simplifier l'écriture de l'algorithme PC, on peut définir une opération infixe en raccourci :
$$ T \otimes S = \texttt{t ** s}.$$ *)
(* In[106]: *)
let ( ** ) = compositions;;
(* #### Union
On peut aussi rapidement définier $T \cup S$, pour l'union. C'est très facile. *)
(* In[107]: *)
let union (t : intervalles) (s : intervalles) : intervalles =
List.append t s
;;
(* #### Exemples
On aimerait reproduire les exemples de la Figure 2 du texte.
 *)
(* - Pour les deux intervalles de la Figure 2.a) : $T_a = \{ [1, 4], [6, 8] \}$ et $S_a = \{ [0, 1], [3, 5], [6, 7] \}$. *)
(* In[108]: *)
t_a ++ s_a;;
(* On retrouve bien le résultat de la Figure 2.a). *)
(* In[109]: *)
t_a ** s_a;;
union t_a s_a;;
(* - Pour les deux intervalles de la Figure 2.b) : $T_b = \{ [-1, 0], [2, 4] \}$ et $S_b = \{ [0, 1], [4, 4] \}$. *)
(* In[110]: *)
t_b ** s_b;;
(* On retrouve bien le résultat de la Figure 2.b).
L'intervalle $[3, 4]$ est inclus dans $[2, 5]$, donc on devrait ajouter une étape de nettoyage pour donner une forme canonique aux intervalles produit par `composition`. On le fait plus bas. *)
(* In[113]: *)
t_b;;
s_b;;
(* In[114]: *)
t_b ++ s_b;;
union t_b s_b;;
(* On remarque que les intervalles sont bien donnés dans l'ordre croissant, puisqu'on a pensé à trier la sortie des deux fonctions, mais ça ne change rien. *)
(* #### Une étape de plus : ne pas inclure des intervalles inclus dans ceux déjà présents
On va raffiner les fonctions définis ci-dessus en ajoutant un test, sur leur résultat final.
- `est_inclus i j` teste si $I \subseteq J$. *)
(* In[119]: *)
let est_inclus (i : intervalle) (j : intervalle) : bool =
let a = fst i and b = snd i in
let c = fst j and d = snd j in
(* on peut aussi écrire directement
let a, b = i and c, d = j in
pour extraire les valeurs d'un coupe i=(a,b) et j=(c,d)
*)
(* c <= a && b <= d *)
(pluspetiteq_ee c a) && (pluspetiteq_ee b d)
;;
(* In[121]: *)
est_inclus (E(3), E(4)) (E(2), E(5));; (* true *)
est_inclus (E(2), E(5)) (E(3), E(4));; (* false *)
est_inclus (E(1), E(1)) (E(1), E(1));; (* true *);;
(* - `est_inclus_dans_un i acc` teste si $I \subseteq J$ pour **un** $J \neq I \in \mathrm{Acc}$. *)
(* In[122]: *)
let est_inclus_dans_un (i : intervalle) (acc : intervalles) : bool =
List.exists (fun j -> (i != j) && (est_inclus i j)) acc
;;
(* - On peut écrire une fonction `filtre` qui retire les intervalles inclus dans d'autres, puis retire les doublons. *)
(* In[123]: *)
let retire_les_inclus (liste : intervalles) : intervalles =
List.filter (fun i -> not (est_inclus_dans_un i liste)) liste
;;
let retire_les_doublons (liste : intervalles) : intervalles =
let reponse = ref [] in
List.iter (fun i ->
if not (List.mem i !reponse) then
reponse := i :: !reponse
) liste;
!reponse
;;
let filtre liste =
retire_les_doublons (retire_les_inclus liste)
;;
(* - L'intersection ne devrait pas être impactée. *)
(* In[124]: *)
let intersections2 (t : intervalles) (s : intervalles) : intervalles =
List.sort compare (filtre (intersections t s))
(* On trie pour les avoir en ordre croissant, c'est tout *)
;;
(* In[125]: *)
let ( ++ ) = intersections2;;
t_a ++ s_a;;
(* - Mais la composition va donner la bonne réponse désormais pour l'exemple de la figure 2.b). *)
(* In[126]: *)
let compositions2 (t : intervalles) (s : intervalles) : intervalles =
List.sort compare (filtre (compositions t s))
(* On trie pour les avoir en ordre croissant, c'est tout *)
;;
(* In[127]: *)
let ( ** ) = compositions2;;
t_b ** s_b;;
(* > C'était un peu long, mais c'est propre au moins. *)
(* Notez que pour obtenir une vraie forme canonique, il faudrait aussi rassembler les intervalles consécutifs ($\{ [0, 1], [1, 2] \} \rightarrow \{ [0, 1] \}$) et se recoupant ($\{ [0, 3], [2, 4] \} \rightarrow \{ [0, 4] \}$).
> Ça prendrait trop de temps. Et ce n'était pas exigé. *)
(* ----
### L'algorithme PC *)
(* #### Structure de données pour les réseaux STP
On a besoin désormais de considérer des réseaux STP, qui sont des graphes dont les sommets sont des entiers, et dont les arêtes sont étiquetées par des *listes* (non vides) d'intervalles.
L'algorithme PC demande de pouvoir accéder rapidement et facilement à l'arête entre deux sommets $x,y$, $T_{x,y}$.
Ainsi, la structure de matrice d'adjacence semble appropriée.
Les arêtes inexistantes dans le réseau auront simplement $T_{x,y} = \emptyset$, c'est-à-dire `[]` (liste vide).
> On supposera que toutes les matrices données aux différentes fonctions définies plus bas sont carrées, on ne le vérifie pas (mais ce serait facile). *)
(* In[128]: *)
type sommet = int;;
type arete = intervalles;; (* c'est l'idée *)
type reseauSTP = intervalles array array;;
(* On essaie tout de suite notre structure de données avec l'exemple du réseau STP de la figure 4 : *)
(* In[235]: *)
let t_01 : intervalles = [(E(0), E(1)); (E(10), E(20))];;
let t_12 : intervalles = [(E(0), E(10))];;
let t_13 : intervalles = [(E(25), E(50))];;
let t_23 : intervalles = [(E(0), E(20)); (E(40), E(40))];;
let t_vide = [(MInf, PInf)];;
let stp_4 : reseauSTP = [|
[| t_vide; t_01; t_vide; t_vide |];
[| t_vide; t_vide; t_12; t_13 |];
[| t_vide; t_vide; t_vide; t_23 |];
[| t_vide; t_vide; t_vide; t_vide |];
|];;
(* On peut vérifier qu'il n'est pas distributif, en prenant l'exemple du texte (fin page 8) : *)
(* In[236]: *)
let s_13 = t_12 ** t_23;;
t_13 ++ s_13;;
t_01 ** (t_13 ++ s_13);; (* 1er cas *)
t_01 ** t_13;;
t_01 ** s_13;;
(t_01 ** t_13) ++ (t_01 ** s_13);; (* 2nd cas *);;
(* En simplifiant, on obtient :
- $T_{01} \otimes (T_{13} \oplus S_{13} = \{ [25, 31], [35, 70] \}$,
- $(T_{01} \otimes T_{13}) \oplus (T_{01} \otimes S_{13}) = \{ [25, 70] \}$,
qui sont bien différents. *)
(* Enfin, on peut rapidement vérifier si la matrice d'un graphe est bien carrée : *)
(* In[237]: *)
let est_carree matrice =
let n = Array.length matrice in
Array.fold_left (fun b x -> b && (n = (Array.length x))) true matrice
;;
(* In[238]: *)
est_carree stp_4;;
(* #### L'algorithme PC
Ça semble être un bon choix.
Maintenant, passons à l'algorithme PC.
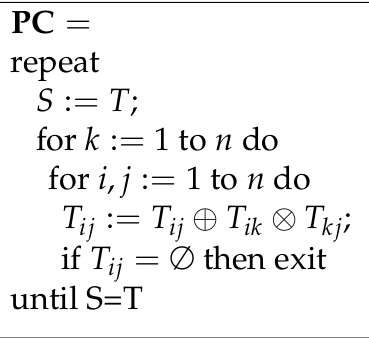. *)
(* Il n'y a pas de boucle `until` en Caml, mais avec une boucle `while` on arrivera presque à la même chose. *)
(* In[239]: *)
exception Fini;; (* Pour faire le [exit]. *);;
(* On peut l'écrire avant pour la rendre plus claire, mais l'étape clé de l'algorithme PC (et Floyd-Warshall) est une opération dite de *relaxation* :
$$ T_{i,j} \oplus (T_{i,k} \otimes T_{k,j}).$$ *)
(* In[240]: *)
let relaxe (reseau : reseauSTP) i j k =
let t_ij = reseau.(i).(j)
and t_ik = reseau.(i).(k)
and t_kj = reseau.(k).(j)
in t_ij ++ (t_ik ** t_kj)
;;
(* On a tout ce qu'il faut pour écrire l'algorithme.
Mais comme il ne marche pas encore, on va le débogguer. *)
(* In[241]: *)
let string_of_entieretendu = function
| MInf -> "-oo"
| PInf -> "+oo"
| E(x) -> string_of_int x
;;
(* In[242]: *)
let print_intervalle (une_contrainte : intervalle) =
let a, b = une_contrainte in
Printf.printf "(%s, %s) " (string_of_entieretendu a) (string_of_entieretendu b)
;;
(* In[243]: *)
let print_intervalles (contraintes : intervalles) =
List.iter print_intervalle contraintes
;;
(* In[244]: *)
let flush_force () =
Printf.printf "\n";
flush_all();
Printf.printf "\n";
flush_all();
Printf.printf "\n";
flush_all();
;;
(* In[245]: *)
let print_reseau (reseau : reseauSTP) : unit =
flush_force ();
Printf.printf "\nReseau =\n";
Array.iteri (fun i ligne ->
Array.iteri (fun j case ->
if case != [(MInf, PInf)] then begin
Printf.printf "\n T[i=%i, j=%i] = [" i j;
print_intervalles case;
Printf.printf "]";
end) ligne
) reseau;
flush_all ();
;;
(* In[246]: *)
stp_4;;
(* In[247]: *)
flush_force();;
(* In[248]: *)
print_reseau stp_4;;
(* On est prêt à écrire l'algorithme : *)
(* In[249]: *)
let algorithmePC ?(max_etape=10) (reseau : reseauSTP) : (reseauSTP * intervalles list) =
let resT = Array.map Array.copy reseau in (* on ne modifie pas l'entrée *)
let resS = ref [||] in
let n = Array.length resT in
let allseen = ref [] in (* Pour débogguer, je veux la liste des Tij vus *)
let etape = ref 0 in
begin
try begin
while !etape < max_etape && !resS != resT do
incr etape;
resS := Array.map Array.copy resT; (* S := T *)
for k = 0 to n - 1 do
for i = 0 to n - 1 do
for j = 0 to n - 1 do
Printf.printf "\n\nEtape %i, k = %i, i = %i, j = %i.\n" !etape k i j;
print_string "Contraintes :";
print_reseau resT;
resT.(i).(j) <- relaxe resT i j k;
allseen := (resT.(i).(j)) :: !allseen; (* on l'ajoute *)
if resT.(i).(j) = [] then
raise Fini
done
done
done
done;
end
with Fini -> () (* On ignore l'exception, on a juste terminé. *)
end;
resT, !allseen
;;
(* ----
### Exemple de réseau non distributif
On va traiter l'exemple de la Figure 4 du texte, comme défini plus haut :
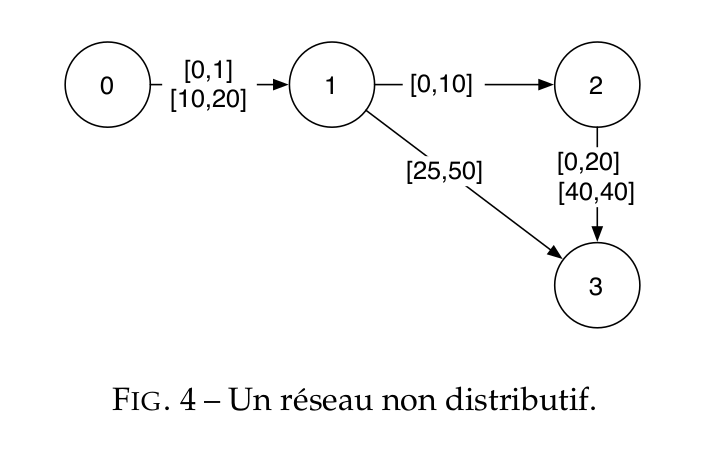 *)
(* In[250]: *)
stp_4;;
(* In[251]: *)
relaxe stp_4 1 2 3;;
(* In[252]: *)
stp_4.(1).(3);;
(* In[ ]: *)
;;
(* In[253]: *)
algorithmePC stp_4;;
(* > Je ne suis pas sûr de comment interprêter ce résultat...
>
> - soit j'ai fait une erreur dans l'implémentation,
> - soit l'algorithme PC devait ne rien modifier à $T$ sur cet exemple... *)
(* ----
### D'autres exemples
On peut étudier le STP de la Figure 1., en enlevant la contrainte $[60, \infty)$, qui ne rentre pas dans notre implémentation.
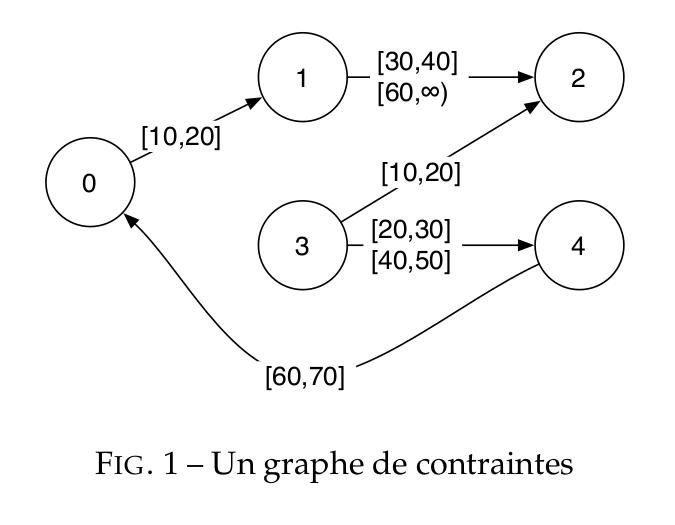. *)
(* In[254]: *)
let t_01 : intervalles = [(E(10), E(20))];;
let t_12 : intervalles = [(E(30), E(40))];;
let t_32 : intervalles = [(E(10), E(20))];;
let t_34 : intervalles = [(E(20), E(30)); (E(40), E(50))];;
let t_40 : intervalles = [(E(60), E(70))];;
let stp_1 : reseauSTP = [|
[| t_vide; t_01; t_vide; t_vide; t_vide |];
[| t_vide; t_vide; t_12; t_vide; t_vide |];
[| t_vide; t_vide; t_vide; t_vide; t_vide |];
[| t_vide; t_vide; t_32; t_vide; t_34 |];
[| t_40; t_vide; t_vide; t_vide; t_vide |];
|];;
(* In[255]: *)
print_reseau stp_1;;
(* In[256]: *)
algorithmePC stp_1;;
(* > Je ne suis pas sûr de comment interprêter ce résultat...
>
> - soit j'ai fait une erreur dans l'implémentation,
> - soit l'algorithme PC devait ne rien modifier à $T$ sur cet exemple... *)
(* ----
## Conclusion
Voilà pour la question obligatoire de programmation :
- on a décomposé le problème en sous-fonctions,
- on a essayé d'être fainéant, en réutilisant les sous-fonctions,
- on a fait des exemples et *on les garde* dans ce qu'on présente au jury,
- on a testé la fonction exigée sur de petits exemples et sur un exemple de taille réelle (venant du texte)
Et on a essayé de faire *un peu plus*, en implémentant la vérification d'une contrainte de plus.
> Bien-sûr, ce petit notebook ne se prétend pas être une solution optimale, ni exhaustive. *)