Exercices sur les méthodes numériques ¶

5ème TD, sur les méthodes numériques.

TD5 au Lycée Lakanal (sujet rédigé par Arnaud Basson).

Traite de la méthode d’Euler (tension(), tension_ordre2()) et du pivot de Gauss (cas tridiagonale, pivotTridiag()).

Date : vendredi 18 décembre 2015,
Auteur : Lilian Besson, pour le cours d’informatique pour tous en prépa MP (http://perso.crans.org/besson/infoMP/),
Licence : MIT Licence (http://lbesson.mit-license.org).

exos_num.tension(h, tmax, ue, R, C)[source]¶

Résoud numériquement l’équation différentielle (1) par la méthode d’Euler pour \(t \in [0, t_{max}]\) avec un pas de temps h.

(1)¶\[R C \frac{d u_c}{d t}(t) + u_c(t) = u_e(t)\]

Pour utiliser un schéma d’Euler, il nous faut écrire cette équation sous la forme \(u'(t) = f(t, u)\) :

\[\begin{split}\frac{d u_c}{d t}(t) &= (u_e(t) - u_c(t)) / (R \times C) \\ f(t, u_c(t)) &= (u_e(t) - u_c(t)) / (R \times C)\end{split}\]

Et dès lors, le schéma de mise à jour d’Euler s’écrit :

\[u_{i+1} = u_i + (t_{i+1} - t_i) \times f(t_i, u_i)\]

Renvoit un tableau (list) contenant les valeurs de \(u_c\) calculées aux instants \(t_i = i \times h\) (pour \(0 \leq i \leq t_{max} / h)\).
Arguments :
- h est un un pas de temps (\(h > 0\)),
- tmax est la durée totale de la simulation numérique (\(t_{max} > 0\)),
- et ue est une fonction \(u_e t \mapsto u_e(t)\), est la tension d’entrée (tension aux bornes de l’ensemble résistance + condensateur).
Hypothèse : On résoudra l’équation pour \(t > 0\) en supposant qu’à \(t = 0\) le condensateur est déchargé (\(u_c(0) = 0\)).
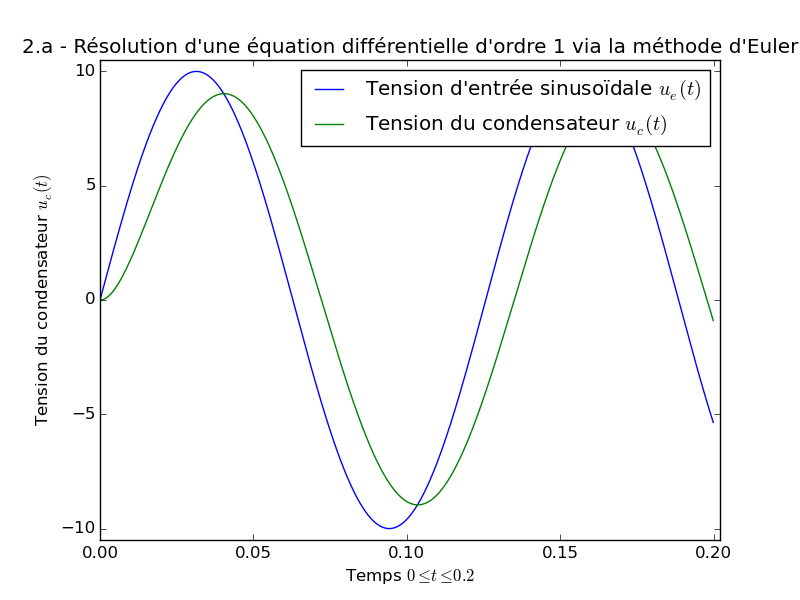
Exemple (question 2.a), avec une tension d’entrée sinusoïdale :

>>> R = 1e6; C = 10e-9
>>> tmax = 0.2
>>> h = tmax / 1000  # On choisit 1000 points
>>> uemax = 10; freq = 50
>>> ue = lambda t: uemax * np.sin(t * freq)
>>> ue(tmax)
-5.4402111088936973
>>> uc = tension(h, tmax, ue, R, C)
>>> uc[-1]
-0.89989324797564696

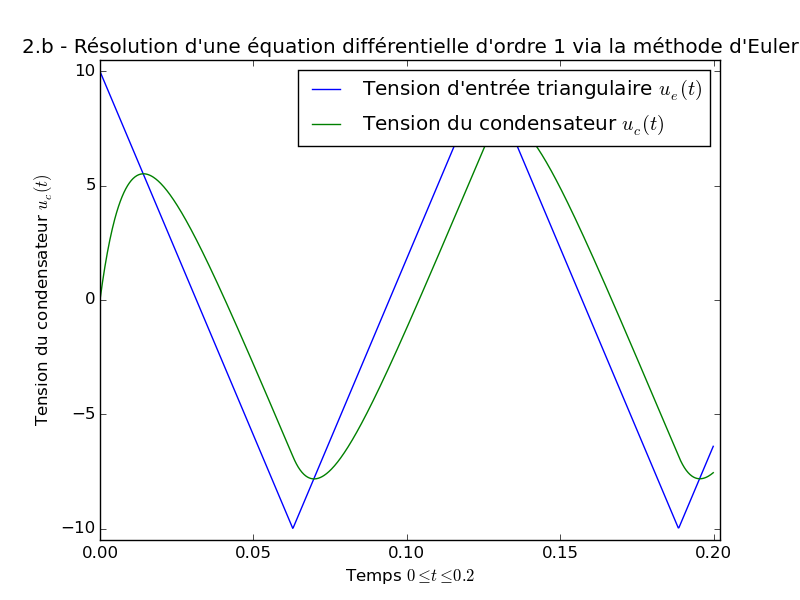
Exemple (question 2.b), avec une tension d’entrée triangulaire.

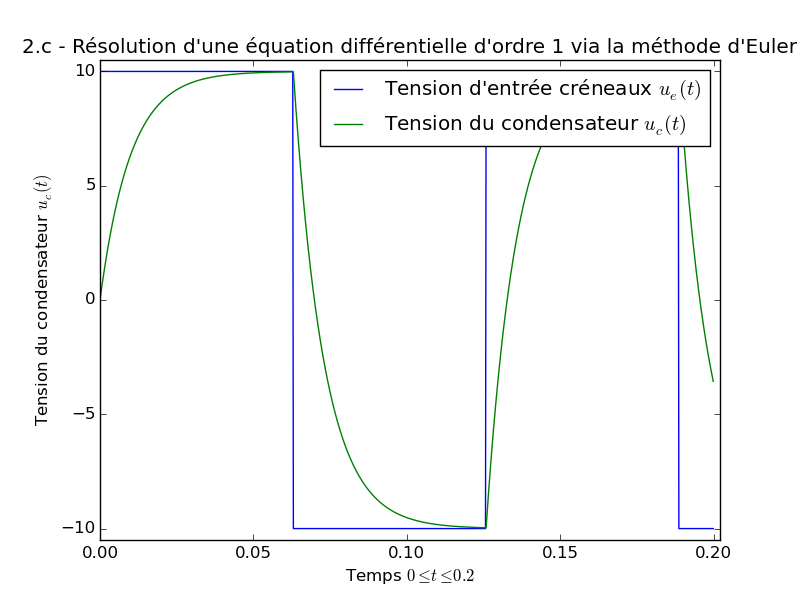
Exemple (question 2.c), avec une tension d’entrée créneaux :

>>> R = 1e6; C = 10e-9
>>> tmax = 0.2
>>> h = tmax / 1000  # On choisit 1000 points
>>> uemax = 10; freq = 50
>>> ue = lambda t: uemax * np.sin(1e-12 + t * freq) / np.abs(np.sin(1e-12 + t * freq))
>>> ue(tmax)
-10.0
>>> uc = tension(h, tmax, ue, R, C)
>>> uc[-1]
-3.5593830469494541

Note

Pour plus de détails sur les circuits RC, voir cette page.

exos_num.tension_ordre2(h, tmax, ue, R, L, C)[source]¶

Résoud numériquement l’équation différentielle d’ordre 2 (2) par la méthode d’Euler pour \(t \in [0, t_{max}]\) avec un pas de temps h.

(2)¶\[L C \frac{d^2 u_c}{d t^2}(t) + R C \frac{d u_c}{d t}(t) + u_c(t) = u_e(t)\]

Pour utiliser un schéma d’Euler, il nous faut écrire cette équation (linéaire d’ordre 2) sous la forme \(U'(t) = f(t, U)\), où \(U = [u, u']\) :

\[\begin{split}U(t) &= [ u_c(t), \frac{d u_c}{d t}(t) ] \\ U(t) &= \Bigl[\begin{smallmatrix} u_c(t) \\ \frac{d u_c}{d t}(t) \end{smallmatrix} \Bigr] \;\;\text{(comme un vecteur)} \\ \frac{d U}{d t}(t) &= \Bigl[ U[2](t), (u_e(t) - U[1](t))/(L\times C) - R/L \times U[2](t) \Bigr] \\ F(t, U) &= \Bigl[ U[2](t), (u_e(t) - U[1](t))/(L \times C) - R/L \times U[2](t) \Bigr]\end{split}\]

Et dès lors, le schéma de mise à jour d’Euler s’écrit :

\[U_{i+1} = U_i + (t_{i+1} - t_i) \times F(t_i, U_i)\]

Cette fois l’opérateur \(F: (t, U) \mapsto f(t, U)\) est vectoriel (de taille \(2 \times 2\)), et affine de qui plus est (mais ça n’a aucune importance !).
Renvoit un tableau (list) contenant les valeurs de \(u_c\) calculées aux instants \(t_i = i \times h\) (pour \(0 \leq i \leq t_{max} / h)\).
Arguments :
- h est un un pas de temps (\(h > 0\)),
- tmax est la durée totale de la simulation numérique (\(t_{max} > 0\)),
- et ue est une fonction \(u_e t \mapsto u_e(t)\), est la tension d’entrée (tension aux bornes de l’ensemble résistance + condensateur).
Hypothèse : On résoudra l’équation pour \(t > 0\) en supposant qu’à \(t = 0\) le condensateur est déchargé (\(u_c(0) = 0\)) et que \(\frac{d u_c}{d t}(t=0) = 0\) aussi (sinon il nous faut une condition numérique précise).
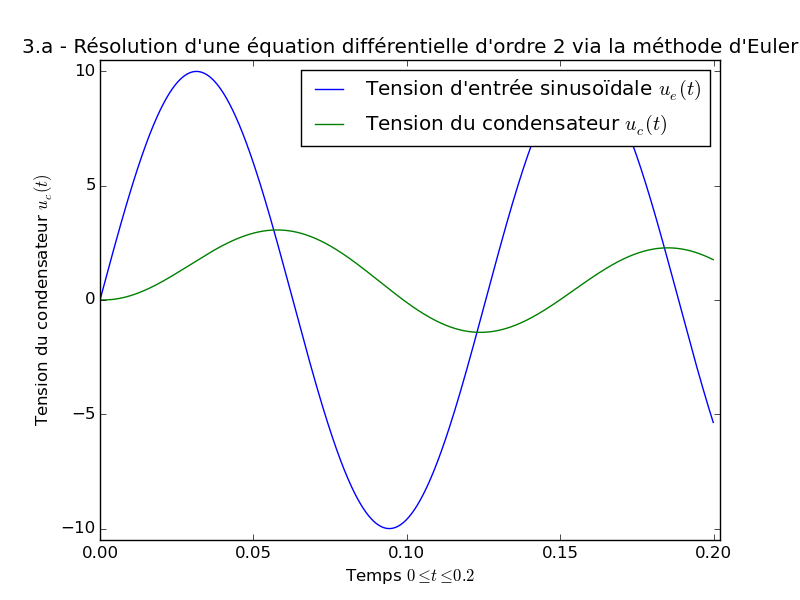
Exemple (question 3.a), avec une tension d’entrée sinusoïdale :

>>> R = 1e3; L = 1; C = 100e-6
>>> tmax = 0.2
>>> h = tmax / 1000  # On choisit 1000 points
>>> uemax = 10; freq = 50
>>> ue = lambda t: uemax * np.sin(t * freq)
>>> ue(tmax)
-5.4402111088936973
>>> # Pour un circuit RC (ordre 1) :
>>> uc = tension(h, tmax, ue, R, C)
>>> uc[-1]
1.686614450937342
>>> # Pour un circuit RLC (ordre 2) :
>>> uc = tension_ordre2(h, tmax, ue, R, L, C)
>>> uc[-1]  # Moins d'atténuation
1.7632486787067487

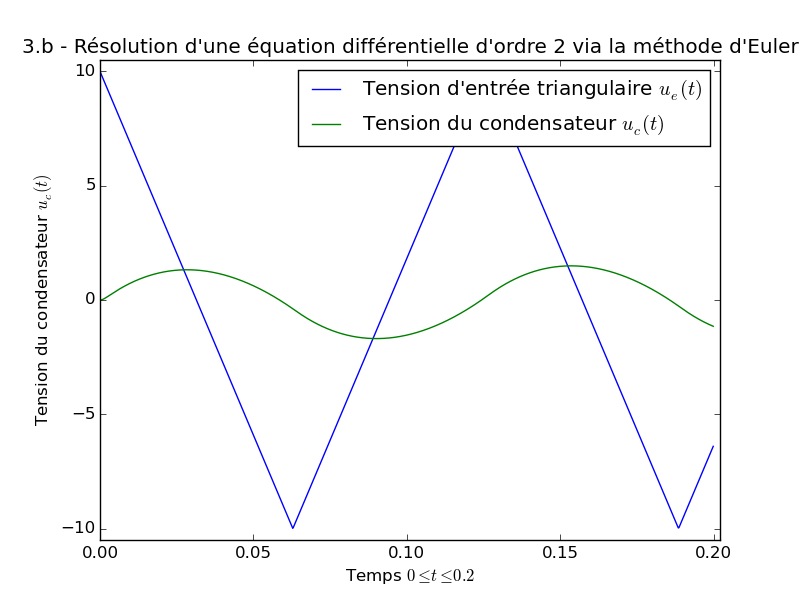
Exemple (question 3.b), avec une tension d’entrée triangulaire.

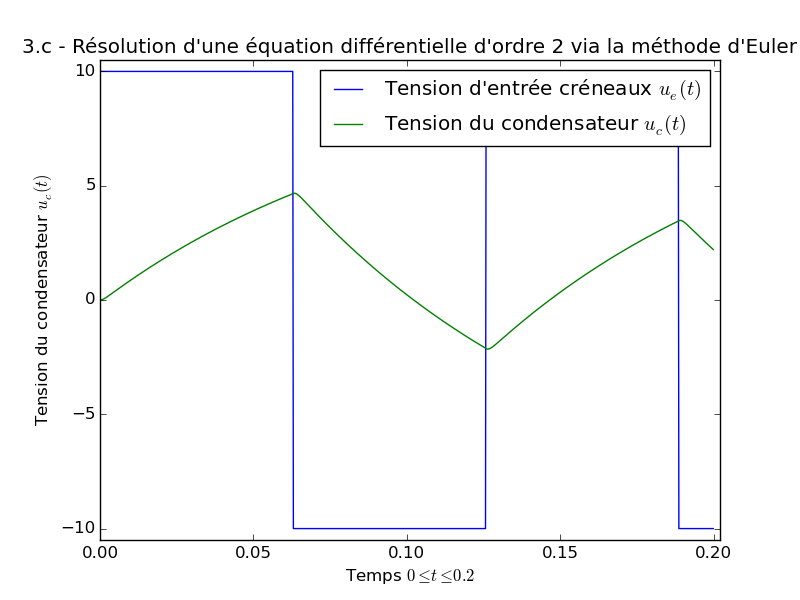
Exemple (question 3.c), avec une tension d’entrée créneaux :

>>> R = 1e3; L = 1; C = 100e-6
>>> tmax = 0.2
>>> h = tmax / 1000  # On choisit 1000 points
>>> uemax = 10; freq = 50
>>> ue = lambda t: uemax * np.sin(1e-12 + t * freq) / np.abs(np.sin(1e-12 + t * freq))
>>> ue(tmax)
-10.0
>>> # Pour un circuit RC (ordre 1) :
>>> uc = tension(h, tmax, ue, R, C)
>>> uc[-1]
2.0756606150715764
>>> # Pour un circuit RLC (ordre 2) :
>>> uc = tension_ordre2(h, tmax, ue, R, L, C)
>>> uc[-1]  # Moins d'atténuation
2.2083917041910097

Note

Pour plus de détails sur les circuits RLC, voir cette page.

exos_num.pivotTridiag(A, b, verb=False)[source]¶

Calcule la solution du système linéaire \(Ax = b\), en appliquant l’algorithme du pivot de Gauss, qui se simplifie largement dans le cas tridiagonal.

Hypothèses : on suppose que A est bien inversible, et qu’aucun échange de ligne n’est nécessaire au cours de la résolution du système linéaire.
Arguments :
- A : matrice tridiagonale, de taille \(n \times n\), supposée inversible,
- b : un vecteur b de taille \(n\) (ie. \(b \in \mathbb{R}^n\)).
Complexité temporelle : \(O(n)\),
Complexité mémoire : \(O(n^2)\).
Exemple :

>>> A = np.array([[ 1, -2,  0], [ 3,  4, -5], [ 0,  6,  7]])
>>> b = np.array([-1, -1, 0])
>>> x = pivotTridiag(A, b)
>>> x
array([-0.72,  0.14, -0.12])

exos_num.lireMatriceA(nomFichier)[source]¶

Lit la matrice A stockée dans le fichier nomFichier, en suivant le format décrit dans l’énoncé.

Les coefficients de la matrice \(A\) sont stockés dans un fichier texte nomFichier (e.g. matrice.txt).
La première ligne du fichier contient la valeur de \(n\) et les \(3n - 2\) lignes suivantes contiennent les valeurs des \(a_k\) , puis des \(b_k\) puis des \(c_k\) , à raison d’un seul coefficient par ligne.

Interlude sur la lecture et écriture de fichiers texte en python :

On créé deux fichiers inutiles pour tester leur lecture et écriture (juste une démo).

$ echo "Fichier en lecture" > /tmp/read.txt
$ echo "Fichier en ecriture (ecrase)" > /tmp/write.txt

On rappelle qu’il faut utiliser la fonction open() pour ouvrir un fichier, en mode "w" pour écrire (write) ou "r" pour lire (read) :

>>> fichierEcriture = open("/tmp/write.txt",  "w")
>>> fichierEcriture.write("Ecrase!")  # Renvoit le nombre de caracteres ecrits
7
>>> fichierLecture  = open("/tmp/read.txt", "r")
>>> print(fichierLecture.readline())
OK

$ echo cat /tmp/write.txt  # Le contenu a change
cat /tmp/write.txt

Retour sur l’écriture d’une matrice :

Exemple : le fichier exos_num_matrice_A.txt contient un matrice tridiagonale \(A\) de taille \(3 \times 3\) :

\[\begin{split}A = \Bigl[\begin{smallmatrix} 1 & -2 & 0 \\ 3 & 4 & -5 \\ 0 & 6 & 7 \end{smallmatrix} \Bigr]\end{split}\]

$ echo "Contenu du fichier 'exos_num_matrice_A.txt' :"
$ cat exos_num_matrice_A.txt
Contenu du fichier 'exos_num_matrice_A.txt' :
3
1
-2
3
4
-5
6
7

On peut donc lire le contenu du fichier et le sauvegarder dans la matrice (numpy array) A :

>>> A = lireMatriceA("exos_num_matrice_A.txt")
>>> A
array([[ 1., -2.,  0.],
       [ 3.,  4., -5.],
       [ 0.,  6.,  7.]])

Note

Plus généralement, numpy propose les fonctions numpy.loadtxt() (numpy.loadtxt (doc)) et numpy.savetxt() (numpy.savetxt (doc)) pour lire et sauvegarder des array dans un fichier texte (extension .txt).

Et un format encore plus compressé (espace réduit, sauvegarde et lecture plus rapides) est un format binaire spécialisé (extension .npy), utilisable avec les fonctions numpy.load() (numpy.load (doc)) et numpy.save() (numpy.save (doc)). Voir cette page pour plus de détails ou cette page pour d’autres méthodes (en anglais).

Note : ces notions plus avancées sont hors programme, bien sûr.

exos_num.enregistrerSolution(A, b, nomFichier)[source]¶

Prenant en arguments une matrice tridiagonale inversible A, un vecteur b et le nom d’un fichier, qui calcule la solution du système Ax = b puis écrit dans le fichier indiqué les valeurs des coefficients de x (un coefficient par ligne).

Attention : le contenu du fichier nomFichier sera écrasé !
Exemple : résolution et sauvegarde de la solution d’un système linéaire de taille \(3\) :

>>> import numpy as np
>>> A = lireMatriceA("exos_num_matrice_A.txt")
>>> A
array([[ 1., -2.,  0.],
       [ 3.,  4., -5.],
       [ 0.,  6.,  7.]])
>>> b = np.array([-1, -1, 0])
>>> x = pivotTridiag(A, b)
>>> x
array([-0.72,  0.14, -0.12])
>>> enregistrerSolution(A, b, 'exos_num_vecteur_x.txt')
Le vecteur x = [-0.72  0.14 -0.12] a bien ete sauvegarde dans le fichier 'exos_num_vecteur_x.txt'.

Le fichier exos_num_vecteur_x.txt contient désormais un vecteur de taille \(3\) :

$ echo "Contenu du fichier 'exos_num_vecteur_x.txt' :"
$ cat exos_num_vecteur_x.txt
Contenu du fichier 'exos_num_vecteur_x.txt' :
3
-0.72
0.14
-0.12

Sortie du script¶

$ python3 exos_num.py


Exercice 1 : Circuits RC et RLC


Exercice 2 : Le pivot de Gauss pour une matrice tridiagonale
Test automatique de toutes les doctests ecrites dans la documentation (docstring) de chaque fonction :
Trying:
    import numpy as np
Expecting nothing
ok
Trying:
    A = lireMatriceA("exos_num_matrice_A.txt")
Expecting nothing
ok
Trying:
    A
Expecting:
    array([[ 1., -2.,  0.],
           [ 3.,  4., -5.],
           [ 0.,  6.,  7.]])
ok
Trying:
    b = np.array([-1, -1, 0])
Expecting nothing
ok
Trying:
    x = pivotTridiag(A, b)
Expecting nothing
ok
Trying:
    x
Expecting:
    array([-0.72,  0.14, -0.12])
**********************************************************************
File "exos_num.py", line 484, in __main__.enregistrerSolution
Failed example:
    x
Expected:
    array([-0.72,  0.14, -0.12])
Got:
    array([-1.,  0.,  0.])
Trying:
    enregistrerSolution(A, b, 'exos_num_vecteur_x.txt')
Expecting:
    Le vecteur x = [-0.72  0.14 -0.12] a bien ete sauvegarde dans le fichier 'exos_num_vecteur_x.txt'.
**********************************************************************
File "exos_num.py", line 486, in __main__.enregistrerSolution
Failed example:
    enregistrerSolution(A, b, 'exos_num_vecteur_x.txt')
Expected:
    Le vecteur x = [-0.72  0.14 -0.12] a bien ete sauvegarde dans le fichier 'exos_num_vecteur_x.txt'.
Got:
    Le vecteur x = [-1.  0.  0.] a bien ete sauvegarde dans le fichier 'exos_num_vecteur_x.txt'.
Trying:
    fichierEcriture = open("/tmp/write.txt",  "w")
Expecting nothing
ok
Trying:
    fichierEcriture.write("Ecrase!")  # Renvoit le nombre de caracteres ecrits
Expecting:
    7
ok
Trying:
    fichierLecture  = open("/tmp/read.txt", "r")
Expecting nothing
ok
Trying:
    print(fichierLecture.readline())
Expecting:
    OK
    <BLANKLINE>
**********************************************************************
File "exos_num.py", line 417, in __main__.lireMatriceA
Failed example:
    print(fichierLecture.readline())
Expected:
    OK
    <BLANKLINE>
Got:
    Fichier en lecture
    <BLANKLINE>
Trying:
    A = lireMatriceA("exos_num_matrice_A.txt")
Expecting nothing
ok
Trying:
    A
Expecting:
    array([[ 1., -2.,  0.],
           [ 3.,  4., -5.],
           [ 0.,  6.,  7.]])
ok
Trying:
    A = np.array([[ 1, -2,  0], [ 3,  4, -5], [ 0,  6,  7]])
Expecting nothing
ok
Trying:
    b = np.array([-1, -1, 0])
Expecting nothing
ok
Trying:
    x = pivotTridiag(A, b)
Expecting nothing
ok
Trying:
    x
Expecting:
    array([-0.72,  0.14, -0.12])
**********************************************************************
File "exos_num.py", line 365, in __main__.pivotTridiag
Failed example:
    x
Expected:
    array([-0.72,  0.14, -0.12])
Got:
    array([-1.,  0.,  0.])
Trying:
    R = 1e6; C = 10e-9
Expecting nothing
ok
Trying:
    tmax = 0.2
Expecting nothing
ok
Trying:
    h = tmax / 1000  # On choisit 1000 points
Expecting nothing
ok
Trying:
    uemax = 10; freq = 50
Expecting nothing
ok
Trying:
    ue = lambda t: uemax * np.sin(t * freq)
Expecting nothing
ok
Trying:
    ue(tmax)
Expecting:
    -5.4402111088936973
ok
Trying:
    uc = tension(h, tmax, ue, R, C)
Expecting nothing
ok
Trying:
    uc[-1]
Expecting:
    -0.89989324797564696
ok
Trying:
    R = 1e6; C = 10e-9
Expecting nothing
ok
Trying:
    tmax = 0.2
Expecting nothing
ok
Trying:
    h = tmax / 1000  # On choisit 1000 points
Expecting nothing
ok
Trying:
    uemax = 10; freq = 50
Expecting nothing
ok
Trying:
    ue = lambda t: uemax * np.sin(1e-12 + t * freq) / np.abs(np.sin(1e-12 + t * freq))
Expecting nothing
ok
Trying:
    ue(tmax)
Expecting:
    -10.0
ok
Trying:
    uc = tension(h, tmax, ue, R, C)
Expecting nothing
ok
Trying:
    uc[-1]
Expecting:
    -3.5593830469494541
ok
Trying:
    R = 1e3; L = 1; C = 100e-6
Expecting nothing
ok
Trying:
    tmax = 0.2
Expecting nothing
ok
Trying:
    h = tmax / 1000  # On choisit 1000 points
Expecting nothing
ok
Trying:
    uemax = 10; freq = 50
Expecting nothing
ok
Trying:
    ue = lambda t: uemax * np.sin(t * freq)
Expecting nothing
ok
Trying:
    ue(tmax)
Expecting:
    -5.4402111088936973
ok
Trying:
    uc = tension(h, tmax, ue, R, C)
Expecting nothing
ok
Trying:
    uc[-1]
Expecting:
    1.686614450937342
ok
Trying:
    uc = tension_ordre2(h, tmax, ue, R, L, C)
Expecting nothing
ok
Trying:
    uc[-1]  # Moins d'atténuation
Expecting:
    1.7632486787067487
ok
Trying:
    R = 1e3; L = 1; C = 100e-6
Expecting nothing
ok
Trying:
    tmax = 0.2
Expecting nothing
ok
Trying:
    h = tmax / 1000  # On choisit 1000 points
Expecting nothing
ok
Trying:
    uemax = 10; freq = 50
Expecting nothing
ok
Trying:
    ue = lambda t: uemax * np.sin(1e-12 + t * freq) / np.abs(np.sin(1e-12 + t * freq))
Expecting nothing
ok
Trying:
    ue(tmax)
Expecting:
    -10.0
ok
Trying:
    uc = tension(h, tmax, ue, R, C)
Expecting nothing
ok
Trying:
    uc[-1]
Expecting:
    2.0756606150715764
ok
Trying:
    uc = tension_ordre2(h, tmax, ue, R, L, C)
Expecting nothing
ok
Trying:
    uc[-1]  # Moins d'atténuation
Expecting:
    2.2083917041910097
ok
1 items had no tests:
    __main__
2 items passed all tests:
  16 tests in __main__.tension
  20 tests in __main__.tension_ordre2
**********************************************************************
3 items had failures:
   2 of   7 in __main__.enregistrerSolution
   1 of   6 in __main__.lireMatriceA
   1 of   4 in __main__.pivotTridiag
53 tests in 6 items.
49 passed and 4 failed.
***Test Failed*** 4 failures.
**********************************************************************
File "exos_num.py", line 484, in __main__.enregistrerSolution
Failed example:
    x
Expected:
    array([-0.72,  0.14, -0.12])
Got:
    array([-1.,  0.,  0.])
**********************************************************************
File "exos_num.py", line 486, in __main__.enregistrerSolution
Failed example:
    enregistrerSolution(A, b, 'exos_num_vecteur_x.txt')
Expected:
    Le vecteur x = [-0.72  0.14 -0.12] a bien ete sauvegarde dans le fichier 'exos_num_vecteur_x.txt'.
Got:
    Le vecteur x = [-1.  0.  0.] a bien ete sauvegarde dans le fichier 'exos_num_vecteur_x.txt'.
**********************************************************************
File "exos_num.py", line 417, in __main__.lireMatriceA
Failed example:
    print(fichierLecture.readline())
Expected:
    OK
    <BLANKLINE>
Got:
    Fichier en lecture
    <BLANKLINE>
**********************************************************************
File "exos_num.py", line 365, in __main__.pivotTridiag
Failed example:
    x
Expected:
    array([-0.72,  0.14, -0.12])
Got:
    array([-1.,  0.,  0.])
**********************************************************************
3 items had failures:
   2 of   7 in __main__.enregistrerSolution
   1 of   6 in __main__.lireMatriceA
   1 of   4 in __main__.pivotTridiag
***Test Failed*** 4 failures.

Plus de details sur ces doctests peut etre trouve dans la documentation de Python:
https://docs.python.org/3/library/doctest.html (en anglais)

Le fichier Python se trouve ici : exos_num.py.

Exercices sur les méthodes numériques¶

Sortie du script¶

Exercices sur les méthodes numériques ¶