Table of Contents¶
ALGO1 : Introduction à l'algorithmique¶
- Page du cours : https://perso.crans.org/besson/teach/info1_algo1_2019/
- Magistère d'Informatique de Rennes - ENS Rennes - Année 2019/2020
- Intervenants :
- Cours : Lilian Besson
- Travaux dirigés : Raphaël Truffet
- Références :
Cours Magistral 9¶
Ce cours traite de programmation linéaire.
On va illustrer deux programmes linéaires résolus avec la fonction
scipy.optimize.linprog.
In [1]:
import numpy as np
import matplotlib.pyplot as plt
import scipy.optimize as opt
Documentation de scipy.opt.linprog¶
In [8]:
print("\n".join(opt.linprog.__doc__.split("\n")[:31]))
La programmation linéaire résout des problèmes de la forme suivante :
$$ \begin{align} \min_x \ & c^T x \\ \mbox{such that} \ & A_{ub} x \leq b_{ub},\\ & A_{eq} x = b_{eq},\\ & l \leq x \leq u , \end{align} $$avec $x$ un vecteur de variables de décisions ; $c$, $b_{ub}$, $b_{eq}$, $l$, et $u$ sont des vecteurs ; $A_{ub}$ et $A_{eq}$ sont des matrices.
Fonction de débogage¶
In [16]:
def make_callback():
list_of_x, list_of_fun = [], []
def debug_callback(opt_res):
print("\nA new optimization step gave:")
print(f"Current solution x = {opt_res.x}")
list_of_x.append(opt_res.x)
print(f"Current value of c @ x = {opt_res.fun}")
list_of_fun.append(opt_res.fun)
print(f"Success? = {opt_res.success}")
print(f"The (nominally positive) values of the slack, b_ub - A_ub @ x. = {opt_res.slack}")
print(f"The (nominally zero) residuals of the equality constraints, b_eq - A_eq @ x. = {opt_res.con}")
print(f"Algorithm in phase {opt_res.phase}")
print(f"Algorithm in iteration number {opt_res.nit}")
status = {
0: "Optimization proceeding nominally.",
1: "Iteration limit reached.",
2: "Problem appears to be infeasible.",
3: "Problem appears to be unbounded.",
4: "Numerical difficulties encountered.",
}
print(f"Algorithm status {status[opt_res.status]}")
if opt_res.message: print(f"Algorithm message: {opt_res.message}")
return list_of_x, list_of_fun, debug_callback
Premier exemple¶
On va suivre l'exemple détaillé en cours :
Variables
- $x$ nombre de tables fabriquées par semaine,
- $y$ nombre de chaises fabriquées par semaine.
Objectif :
- maximiser $30x + 10y$.
Contraintes :
- heures de travail : $6x+3y \leq 36$,
- demande : $y \geq 3x$,
- stockage : $x + y/4 \leq 4$,
- positivité : $x \geq 0$,
- positivité : $y \geq 0$.
Mise sous la forme requise par la fonction linprog, cela va donner :
Et donc avec Python cela sera :
In [10]:
c = np.array([-30, -10])
A_ub = np.array([[6, 3], [3, -1], [1, 1/4]])
b_ub = np.array([36, 0, 4])
A_eq = None
b_eq = None
# all variables are bound to be in (0, +inf)
bounds = (0, None)
Objectif :
In [11]:
import sympy
x, y = sympy.var('x y')
In [12]:
c.T @ [x, y]
Out[12]:
Contraintes d'inéqualités :
In [13]:
A_ub @ [x, y]
Out[13]:
In [14]:
b_ub
Out[14]:
Essayons avec différentes méthodes de résolution :
In [17]:
list_of_x, list_of_fun, debug_callback = make_callback()
opt.linprog(c,
A_ub=A_ub, b_ub=b_ub,
A_eq=A_eq, b_eq=b_eq,
bounds=bounds,
method="simplex",
callback=debug_callback,
)
Out[17]:
In [18]:
x_opt, y_opt = _.x
La solution obtenue est donc $x = 2$ et $y = 8$, qui donnerait un profit maximal de $+140 €$ par semaine en respectant toutes les contraintes.
Pour obtenir une solution entière, on a rien à faire ici.
Si la solution optimale était par exemple $2.23$ et $6.43$, on pourrait essayer $x = 2, 3$ et $y = 6, 7$, ie. on arrondit en dessous et au dessus, et on prend la solution qui satisfait les contraintes et maximise l'objectif :
In [19]:
x_opt, y_opt
Out[19]:
In [20]:
import itertools
In [22]:
sol = None
min_obj = float("+inf")
for (x, y) in itertools.product(
[int(np.floor(x_opt)), int(np.ceil(x_opt))],
[int(np.floor(y_opt)), int(np.ceil(y_opt))],
):
obj = c.T @ [x, y]
ctr = (A_ub @ [x, y]) <= b_ub
print(f"Pour (x, y) = {x, y}, l'objectif vaut {obj}, la contrainte vaut {ctr}")
if np.all(ctr) and obj < min_obj:
min_obj = obj
sol = [x, y]
print(f"==> Donc on utilise la solution entière optimale = {sol}")
La solution entière optimale à ce premier problème est donc de fabriquer $x=2$ tables et $y=8$ chaises chaque semaine.
Second exemple¶
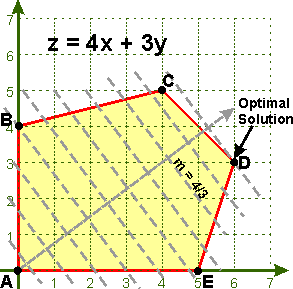
Mise sous la forme requise par la fonction linprog, cela va donner :
Et donc avec Python cela sera :
In [23]:
c = np.array([-4, -3])
A_ub = np.array([[-1, 4], [1, 1], [3, -1]])
b_ub = np.array([16, 9, 15])
A_eq = None
b_eq = None
# all variables are bound to be in (0, +inf)
bounds = (0, None)
Objectif :
In [24]:
import sympy
x, y = sympy.var('x y')
In [25]:
c.T @ [x, y]
Out[25]:
Contraintes d'inéqualités :
In [26]:
A_ub @ [x, y]
Out[26]:
In [27]:
b_ub
Out[27]:
Essayons avec différentes méthodes de résolution :¶
Avec la méthode du simplexe¶
In [38]:
list_of_x, list_of_fun, debug_callback = make_callback()
opt.linprog(c,
A_ub=A_ub, b_ub=b_ub,
A_eq=A_eq, b_eq=b_eq,
bounds=bounds,
method="simplex",
callback=debug_callback,
)
Out[38]:
In [39]:
plt.figure(figsize=(10, 7))
plt.title("Valeur de l'objectif étape par étape (méthode simplexe)")
plt.plot(list_of_fun, "ro-", lw=3, ms=14)
plt.show()
Out[39]:
Out[39]:
Out[39]:
In [40]:
plt.figure(figsize=(10, 7))
plt.title("Position des points étape par étape (méthode simplexe)")
list_of_X, list_of_Y = [x for (x,y) in list_of_x], [y for (x,y) in list_of_x]
# plt.plot(list_of_X, list_of_Y, 'bo-')
plt.plot(list_of_X, 'bo-', label="Valeur de x", lw=3, ms=14)
plt.plot(list_of_Y, 'gd-', label="Valeur de y", lw=3, ms=14)
plt.legend()
plt.show()
Out[40]:
Out[40]:
Out[40]:
Out[40]:
Out[40]:
Avec la méthode du point intérieur (un autre algorithme)¶
Cet autre algorithme est plus récent, plus technique, et il fonctionne généralement mieux : plus rapide, plus stable numérique.
In [41]:
list_of_x, list_of_fun, debug_callback = make_callback()
opt.linprog(c,
A_ub=A_ub, b_ub=b_ub,
A_eq=A_eq, b_eq=b_eq,
bounds=bounds,
method="interior-point",
callback=debug_callback,
)
Out[41]:
In [42]:
plt.figure(figsize=(10, 7))
plt.title("Valeur de l'objectif étape par étape (méthode point intérieur)")
plt.plot(list_of_fun, "ro-", lw=3, ms=14)
plt.show()
Out[42]:
Out[42]:
Out[42]:
In [43]:
plt.figure(figsize=(10, 7))
plt.title("Position des points étape par étape (méthode point intérieur)")
list_of_X, list_of_Y = [x for (x,y) in list_of_x], [y for (x,y) in list_of_x]
# plt.plot(list_of_X, list_of_Y, 'bo-')
plt.plot(list_of_X, 'bo-', label="Valeur de x", lw=3, ms=14)
plt.plot(list_of_Y, 'gd-', label="Valeur de y", lw=3, ms=14)
plt.legend()
plt.show()
Out[43]:
Out[43]:
Out[43]:
Out[43]:
Out[43]:
Bonus : implémentation manuelle de l'algorithme du simplexe¶
- Refs : ce poste de blogue, ces notes de cours, et cet autre poste de blogue.
- Code source venant de : https://github.com/j2kun/simplex-algorithm/
Algorithme¶
In [44]:
import numpy as np
import heapq
In [89]:
def identity(numRows, numCols, val=1, rowStart=0):
""" Return a rectangular identity matrix with the specified diagonal entiries, possibly starting in the middle.
"""
# return val * np.ones((numRows, numCols))
return [
[
(val if i == j else 0)
for j in range(numCols)
]
for i in range(rowStart, numRows)
]
Conversion en forme standard¶
In [90]:
def standardForm(cost,
greaterThans=None, gtThreshold=None,
lessThans=None, ltThreshold=None,
equalities=None, eqThreshold=None,
maximization=True):
"""
standardForm: [float], [[float]], [float], [[float]], [float], [[float]], [float] -> [float], [[float]], [float]
Convert a linear program in general form to the standard form for the
simplex algorithm. The inputs are assumed to have the correct dimensions: cost
is a length n list, greaterThans is an n-by-m matrix, gtThreshold is a vector
of length m, with the same pattern holding for the remaining inputs. No
dimension errors are caught, and we assume there are no unrestricted variables.
"""
newVars = 0
numRows = 0
if gtThreshold:
newVars += len(gtThreshold)
numRows += len(gtThreshold)
if ltThreshold:
newVars += len(ltThreshold)
numRows += len(ltThreshold)
if eqThreshold:
numRows += len(eqThreshold)
if not maximization:
cost = [-x for x in cost]
if newVars == 0:
return cost, equalities, eqThreshold
newCost = list(cost) + ([0] * newVars)
constraints = [ ]
threshold = [ ]
oldConstraints = [(greaterThans, gtThreshold, -1), (lessThans, ltThreshold, 1),
(equalities, eqThreshold, 0)]
offset = 0
for constraintList, oldThreshold, coefficient in oldConstraints:
constraints += [c + r for c, r in zip(constraintList,
identity(numRows, newVars, coefficient, offset))]
threshold += oldThreshold
offset += len(oldThreshold)
return newCost, constraints, threshold
Utilitaires pour les matrices¶
In [91]:
def dot(a, b):
return sum(x*y for x, y in zip(a, b))
In [92]:
def column(A, j):
return [row[j] for row in A]
In [93]:
def transpose(A):
return [column(A, j) for j in range(len(A[0]))]
In [94]:
def isPivotCol(col):
return (len([c for c in col if c == 0]) == len(col) - 1) and sum(col) == 1
def variableValueForPivotColumn(tableau, column):
pivotRow = [i for (i, x) in enumerate(column) if x == 1][0]
return tableau[pivotRow][-1]
In [95]:
# assume the last m columns of A are the slack variables; the initial basis is
# the set of slack variables
def initialTableau(c, A, b):
tableau = [row[:] + [x] for row, x in zip(A, b)]
tableau.append([ci for ci in c] + [0])
return tableau
In [96]:
def primalSolution(tableau):
# the pivot columns denote which variables are used
columns = transpose(tableau)
indices = [j for j, col in enumerate(columns[:-1]) if isPivotCol(col)]
return [(colIndex, variableValueForPivotColumn(tableau, columns[colIndex]))
for colIndex in indices]
In [97]:
def objectiveValue(tableau):
return -(tableau[-1][-1])
In [98]:
def canImprove(tableau):
lastRow = tableau[-1]
return any(x > 0 for x in lastRow[:-1])
In [99]:
# this can be slightly faster
def moreThanOneMin(L):
if len(L) <= 1:
return False
x, y = heapq.nsmallest(2, L, key=lambda x: x[1])
return x == y
In [100]:
def findPivotIndex(tableau):
# pick minimum positive index of the last row
column_choices = [(i, x) for (i, x) in enumerate(tableau[-1][:-1]) if x > 0]
column = min(column_choices, key=lambda a: a[1])[0]
# check if unbounded
if all(row[column] <= 0 for row in tableau):
raise Exception('Linear program is unbounded.')
# check for degeneracy: more than one minimizer of the quotient
quotients = [
(i, r[-1] / r[column])
for i, r in enumerate(tableau[:-1])
if r[column] > 0
]
if moreThanOneMin(quotients):
raise Exception('Linear program is degenerate.')
# pick row index minimizing the quotient
row = min(quotients, key=lambda x: x[1])[0]
return row, column
In [101]:
def pivotAbout(tableau, pivot):
i, j = pivot
pivotDenom = tableau[i][j]
tableau[i] = [x / pivotDenom for x in tableau[i]]
for k,row in enumerate(tableau):
if k != i:
pivotRowMultiple = [y * tableau[k][j] for y in tableau[i]]
tableau[k] = [x - y for x,y in zip(tableau[k], pivotRowMultiple)]
L'algorithme du simplexe¶
In [102]:
def simplex(c, A, b):
"""
simplex: c: [float], A: [[float]], b: [float] -> [float], float
Solve the given standard-form linear program:
max <c, x>
s.t. Ax = b
x >= 0
Providing the optimal solution x* and the value of the objective function.
"""
tableau = initialTableau(c, A, b)
print("Initial tableau:")
for row in tableau:
print(row)
print()
while canImprove(tableau):
pivot = findPivotIndex(tableau)
print("Next pivot index is={}\n".format(pivot))
pivotAbout(tableau, pivot)
print("Tableau after pivot:")
for row in tableau:
print(row)
print()
return tableau, primalSolution(tableau), objectiveValue(tableau)
Un premier exemple¶
In [103]:
c = [300, 250, 450]
A = [[15, 20, 25], [35, 60, 60], [20, 30, 25], [0, 250, 0]]
b = [1200, 3000, 1500, 500]
# add slack variables by hand
A[0] += [1, 0, 0, 0]
A[1] += [0, 1, 0, 0]
A[2] += [0, 0, 1, 0]
A[3] += [0, 0, 0, -1]
c += [0, 0, 0, 0]
t, s, v = simplex(c, A, b)
print(s)
print(v)
Et pou comparer avec la réponse donnée par scipy.optimize.linprog :
In [104]:
opt_res = opt.linprog(-np.array(c), A_ub=A, b_ub=b, method="simplex")
opt_res
Out[104]:
La solution optimale trouvée par scipy.optimize.linprog est meilleure que celle trouvée par notre algorithme.
In [105]:
v, - opt_res.fun
Out[105]:
Notre implémentation donne une solution :
In [106]:
s
Out[106]:
Qui s'interprète comme étant assez proche de la solution trouvée par scipy.optimize.linprog.
In [107]:
opt_res.x
Out[107]:
In [108]:
s2 = np.array([56, 2, 12, 0, 152, 0, 0])
s2
Out[108]:
In [109]:
np.linalg.norm(opt_res.x - s2) / np.linalg.norm(opt_res.x)
Out[109]:
C'est une différence relativement faible…
Tests¶
In [110]:
def test(expected, actual):
e, a = np.array(expected), np.array(actual)
if not np.isclose(np.linalg.norm(e - a), 0):
import sys, traceback
(filename, lineno, container, code) = traceback.extract_stack()[-2]
print("Test: {} failed on line {} in file {}.\nExpected {} but got {}\n".format((code, lineno, filename, expected, actual)))
In [111]:
def testFromPost():
cost = [1, 1, 1]
gts = [[0, 1, 4]]
gtB = [10]
lts = [[3, -2, 0]]
ltB = [7]
eqs = [[1, 1, 0]]
eqB = [2]
expectedCost = [1,1,1,0,0]
expectedConstraints = [[0,1,4,-1,0], [3,-2,0,0,1], [1,1,0,0,0]]
expectedThresholds = [10,7,2]
c, cs, ts = standardForm(cost, gts, gtB, lts, ltB, eqs, eqB)
test(expectedCost, c)
test(expectedConstraints, cs)
test(expectedThresholds, ts)
A_ub = np.array([
[0, 1, 4],
[-3, 2, 0]
])
b_ub = np.array([10, -7])
opt_res = opt.linprog(-np.array(cost),
A_eq=np.array(eqs), b_eq=np.array(eqB),
A_ub=np.array(A_ub), b_ub=np.array(b_ub),
method="simplex")
print("Expected cost", expectedCost)
print("scipy.optimize.linprog gives a solution =", opt_res.x)
In [112]:
testFromPost()
Un second test :
In [113]:
def test2():
cost = [1, 1, 1]
lts = [[3, -2, 0]]
ltB = [7]
eqs = [[1, 1, 0]]
eqB = [2]
expectedCost = [1, 1, 1, 0]
expectedConstraints = [[3, -2, 0, 1], [1 ,1 ,0 ,0]]
expectedThresholds = [7, 2]
test((expectedCost, expectedConstraints, expectedThresholds),
standardForm(cost, lessThans=lts, ltThreshold=ltB, equalities=eqs, eqThreshold=eqB))
In [ ]:
test2()
Un dernier test :
In [115]:
def test3():
cost = [1, 1, 1]
eqs = [[1, 1, 0], [2, 2, 2]]
eqB = [2, 5]
expectedCost = [1, 1, 1]
expectedConstraints = [[3, -2, 0], [1, 1, 0]]
expectedThresholds = [2, 5]
test((expectedCost, expectedConstraints, expectedThresholds),
standardForm(cost, equalities=eqs, eqThreshold=eqB))
In [ ]:
test3()
Ca suffit pour ces exemples.
Conclusion¶
C'est bon pour aujourd'hui !