Table of Contents¶
ALGO1 : Introduction à l'algorithmique¶
- Page du cours : https://perso.crans.org/besson/teach/info1_algo1_2019/
- Magistère d'Informatique de Rennes - ENS Rennes - Année 2019/2020
- Intervenants :
- Cours : Lilian Besson
- Travaux dirigés : Raphaël Truffet
- Références :
Cours Magistral 4 & 5¶
- Ce cours traite de graphes.
On donne le type abstrait des graphes, et plusieurs implémentations de la même structure de données (plusieurs classes).
CM4 : On implémente le parcours en profondeur, qu'on illustre sur quelques exemples.
- CM5 : On implémente le parcours en largeur, qu'on illustre sur quelques exemples.
Type abstrait des $\alpha$ graphes¶
On se donne un type $\alpha$ pour les sommets, et on va en fait se restreindre à $\alpha=$ int, et les sommets seront $\{0,\dots,n-1\}$ où $n = |S|$ pour des graphes $G = (S, A)$.
On va écrire une classe qui implémente des opérations "plus haut niveau", en fonction des opérations bas niveau.
Pour l'afficher, on va utiliser la librarie networkx
In [140]:
import networkx as nx
In [170]:
class BaseGraph():
def out_degree(self, vertex):
return len(self.succ(vertex))
def in_degree(self, vertex):
return len(self.pred(vertex))
def degree(self, vertex):
return len(self.neighbors(vertex))
def is_vertex(self, vertex):
""" Test presence of a vertex."""
return vertex in self.vertexes
@property
def vertexes(self):
""" List of vertexes."""
return list(range(self.nb_vertexes))
def is_neighbor(self, u, v):
""" Test neighborhood."""
return u in self.neighbors(v)
@property
def edges(self):
""" Set of edges (pairs), in O(|A|) if well implemented."""
return {(u, v) for u in self.vertexes for v in self.neighbors(u)}
@property
def nb_edges(self):
return len(self.edges)
def draw(self):
G = nx.DiGraph() if self.oriented else nx.Graph()
G.add_nodes_from(self.vertexes)
G.add_edges_from(self.edges)
return nx.draw_kamada_kawai(G, with_labels=True, font_weight='bold')
Un premier exemple de graphe¶
On va travailler avec le graphe exemple suivant, qu'il soit orienté ou non :
| Orienté | Non orienté |
|---|---|
 |
 |
In [183]:
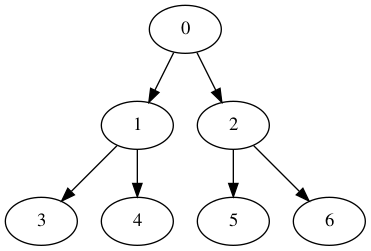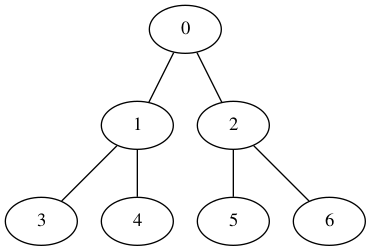def defaultGraph(GraphClass, oriented=True):
print(f"Creating empty graph with class {GraphClass}...")
graph = GraphClass(oriented=oriented)
n = 7
for i in range(n):
print(f"Adding vertex {i}...")
graph.add_vertex(i)
for edge in [(0, 1), (0, 2), (1, 3), (1, 4), (2, 5), (2, 6)]:
print(f"Adding edge {edge}...")
graph.add_edge(*edge)
return graph
In [184]:
plt.figure()
defaultGraph(AdjMatrixGraph, oriented=True).draw()
plt.figure()
defaultGraph(AdjMatrixGraph, oriented=False).draw()
Out[184]:
Out[184]:
On va tester les différentes implémentations avec la petite fonction suivante, qui vérifie que l'on peut accéder à toute l'information contenu dans le graphe.
In [143]:
def test_defaultGraph(GraphClass):
for oriented in [True, False]:
graph = defaultGraph(GraphClass, oriented=oriented)
print(f"Graph:")
print(graph)
print(f"Number of vertexes: {graph.nb_vertexes}")
print(f"Is the graph oriented? {graph.oriented}")
print(f"Number of edges: {graph.nb_edges}")
print(f"List of vertexes: {graph.vertexes}")
print(f"List of edges: {graph.edges}")
for i in graph.vertexes:
print(f" List of neighbors of {i}: {graph.neighbors(i)} (degree {graph.degree(i)})")
print(f" List of succ of {i}: {graph.succ(i)} (out degree {graph.out_degree(i)})")
print(f" List of pred of {i}: {graph.pred(i)} (in degree {graph.in_degree(i)})")
Graphe aléatoire de taille $n$¶
On va étudier un graphe aléatoire suivant un modèle très simple : on fixe $n$ le nombre de sommets, et ensuite chaque arête $(i, j)$ est ajoutée dans le graphe avec une probabilité $p\in(0,1)$ fixée (graphe d'Erdös-Rényi).
In [144]:
import random
In [145]:
def with_probability(p):
return random.random() <= p
In [146]:
def randomGraph(GraphClass, n=10, probability=0.1, oriented=True):
graph = GraphClass(oriented=oriented)
for i in range(n):
graph.add_vertex(i)
for i in range(n):
for j in range(n):
if with_probability(probability):
graph.add_edge(i, j)
return graph
In [147]:
print(randomGraph(AdjMatrixGraph, 10, 0.1, oriented=True))
In [189]:
plt.figure(figsize=(4, 3))
randomGraph(AdjMatrixGraph, 10, 0.1, oriented=True).draw()
Out[189]:
In [190]:
plt.figure(figsize=(4, 3))
randomGraph(AdjMatrixGraph, 10, 0.5, oriented=True).draw()
Out[190]:
In [191]:
plt.figure(figsize=(4, 3))
randomGraph(AdjMatrixGraph, 10, 0.5, oriented=False).draw()
Out[191]:
In [192]:
plt.figure(figsize=(4, 3))
randomGraph(AdjMatrixGraph, 10, 0.9, oriented=True).draw()
Out[192]:
Trois différentes implémentations¶
Graphes par matrice d'adjacence¶
In [173]:
import numpy as np
In [174]:
class AdjMatrixGraph(BaseGraph):
def __init__(self, oriented=True, n=0):
""" Takes O(n^2) time and space."""
self.oriented = oriented
self.nb_vertexes = n
self._matrix = np.zeros((n, n), dtype=bool)
def __str__(self):
return str(self._matrix)
def is_vertex(self, vertex):
""" Test presence of a vertex."""
return 0 <= vertex < self.nb_vertexes
def add_vertex(self, m):
""" Worst case is O(m^2) to extend the matrix. Best case is O(1) if nothing to do."""
if not self.is_vertex(m):
n = self.nb_vertexes
assert 0 <= m and n <= m
self.nb_vertexes = m + 1
old_matrix = self._matrix[:,:]
# extend the matrix
self._matrix = np.zeros((m + 1, m + 1), dtype=bool)
# copy the old matrix
self._matrix[:n, :n] = old_matrix
def add_edge(self, i, j):
""" O(1) time."""
assert 0 <= i < self.nb_vertexes and 0 <= j < self.nb_vertexes
self._matrix[i, j] = True
if not self.oriented:
self._matrix[j, i] = True
def remove_vertex(self, m):
""" TODO do it yourself, it's not hard!"""
raise NotImplementedError
def remove_edge(self, i, j):
""" O(1) time."""
assert 0 <= i < self.nb_vertexes and 0 <= j < self.nb_vertexes
self._matrix[i, j] = False
if not self.oriented:
self._matrix[j, i] = False
def merge_vertexes(self, i, j):
""" TODO do it yourself, it's not hard!"""
raise NotImplementedError
def pred(self, i):
assert 0 <= i < self.nb_vertexes
return [j for j in self.vertexes if self.is_neighbor(j, i)]
def is_pred(self, u, v):
""" O(1) time."""
return self._matrix[v, u]
def succ(self, i):
assert 0 <= i < self.nb_vertexes
return [j for j in self.vertexes if self.is_neighbor(i, j)]
def is_succ(self, u, v):
""" O(1) time."""
return self._matrix[u, v]
def neighbors(self, i):
assert 0 <= i < self.nb_vertexes
if self.oriented:
return self.succ(i)
else:
return [j for j in self.vertexes if self.is_neighbor(i, j) or self.is_neighbor(j, i)]
def is_neighbor(self, u, v):
""" O(1) time."""
if self.oriented:
return self._matrix[u, v]
else:
return self._matrix[u, v] or self._matrix[v, u]
Testons cette première implémentation :
In [175]:
defaultGraph(AdjMatrixGraph)
Out[175]:
In [176]:
test_defaultGraph(AdjMatrixGraph)
Graphes par listes d'adjacence¶
In [177]:
class AdjListsGraph(BaseGraph):
def __init__(self, oriented=True, n=0):
""" Takes O(n) time and space to allocate the empty lists."""
self.oriented = oriented
self.nb_vertexes = n
self._lists = [ [] for i in range(n) ]
def __str__(self):
return str(self._lists)
def is_vertex(self, vertex):
""" Test presence of a vertex."""
return 0 <= vertex < self.nb_vertexes
def add_vertex(self, m):
""" Worst case is O(m^2) to extend the matrix. Best case is O(1) if nothing to do."""
if not self.is_vertex(m):
n = self.nb_vertexes
assert 0 <= m and n <= m
self.nb_vertexes = m + 1
self._lists = [ [] if i >= n else self._lists[i] for i in range(m + 1) ]
def add_edge(self, i, j):
""" O(1) time: append j in head of list of neighbors of i."""
assert 0 <= i < self.nb_vertexes and 0 <= j < self.nb_vertexes
if not self.is_neighbor(i, j):
self._lists[i].append(j)
if not self.oriented:
if not self.is_neighbor(j, i):
self._lists[j].append(i)
def remove_vertex(self, m):
""" TODO do it yourself, it's not hard!"""
raise NotImplementedError
def remove_edge(self, i, j):
""" O(1) time."""
assert 0 <= i < self.nb_vertexes and 0 <= j < self.nb_vertexes
self._lists[i].remove(j)
if not self.oriented:
self._lists[j].remove(i)
def merge_vertexes(self, i, j):
""" TODO do it yourself, it's not hard!"""
raise NotImplementedError
def pred(self, i):
""" Not trivial, has to check all lists, in O(|S|*|A|)."""
assert 0 <= i < self.nb_vertexes
return [j for j in self.vertexes if self.is_pred(j, i)]
def is_pred(self, u, v):
""" O(|S|) time in worst case."""
return u in self._lists[v]
def succ(self, i):
""" Create a new list, to be sure that we don't modify the underlying self._lists. In O(deg(i))."""
assert 0 <= i < self.nb_vertexes
return list(self._lists[i])
def is_succ(self, u, v):
""" O(|S|) time in worst case."""
return v in self._lists[u]
def neighbors(self, i):
assert 0 <= i < self.nb_vertexes
if self.oriented:
return list(self.succ(i))
else:
return [j for j in self.vertexes if self.is_neighbor(i, j)]
def is_neighbor(self, u, v):
""" O(|S|) time in worst case."""
if self.oriented:
return v in self._lists[u]
else:
return v in self._lists[u] or u in self._lists[v]
Testons cette première implémentation :
In [178]:
defaultGraph(AdjListsGraph)
Out[178]:
In [179]:
test_defaultGraph(AdjListsGraph)
Graphes par liste d'arêtes¶
In [180]:
class EdgesListGraph(BaseGraph):
def __init__(self, oriented=True, n=0):
""" Takes O(n) time and space to allocate the empty lists."""
self.oriented = oriented
self.nb_vertexes = n
self._edges = set()
def __str__(self):
return str(self._edges)
def is_vertex(self, vertex):
""" Test presence of a vertex."""
return 0 <= vertex < self.nb_vertexes
def add_vertex(self, m):
""" Worst case is O(m^2) to extend the matrix. Best case is O(1) if nothing to do."""
if not self.is_vertex(m):
n = self.nb_vertexes
assert 0 <= m and n <= m
self.nb_vertexes = m + 1
def add_edge(self, i, j):
""" O(1) time: append j in head of list of neighbors of i."""
assert 0 <= i < self.nb_vertexes and 0 <= j < self.nb_vertexes
if not self.is_neighbor(i, j):
self._edges.add((i, j))
if not self.oriented:
if not self.is_neighbor(j, i):
self._edges.add((j, i))
def remove_vertex(self, m):
""" TODO do it yourself, it's not hard!"""
raise NotImplementedError
def remove_edge(self, i, j):
""" O(1) time."""
assert 0 <= i < self.nb_vertexes and 0 <= j < self.nb_vertexes
self._edges.remove((i, j))
if not self.oriented:
self._edges.remove((j, i))
def merge_vertexes(self, i, j):
""" TODO do it yourself, it's not hard!"""
raise NotImplementedError
def pred(self, i):
assert 0 <= i < self.nb_vertexes
return [j for j in self.vertexes if self.is_pred(j, i)]
def is_pred(self, u, v):
""" O(|S|) time in worst case."""
return (v, u) in self._edges
def succ(self, i):
assert 0 <= i < self.nb_vertexes
return [j for j in self.vertexes if self.is_succ(i, j)]
def is_succ(self, u, v):
""" O(|S|) time in worst case."""
return (u, v) in self._edges
def neighbors(self, i):
assert 0 <= i < self.nb_vertexes
return [j for j in self.vertexes if self.is_neighbor(j, i)]
def is_neighbor(self, u, v):
""" O(|S|) time in worst case."""
if self.oriented:
return (u, v) in self._edges
else:
return (u, v) in self._edges or (v, u) in self._edges
Testons cette première implémentation :
In [181]:
defaultGraph(EdgesListGraph)
Out[181]:
In [182]:
test_defaultGraph(EdgesListGraph)
Test numérique des complexités des différentes opérations¶
On rappelle qu'on devrait obtenir les résultats suivants, avec $n=|S|$ et $m=|A|$, que l'on va valider expérimentalement.
| Opérations | Matrice d'adjacence | Listes d'adjacence | Liste d'arêtes |
|---|---|---|---|
| Création (vide) | temps et mémoire $O(n^2)$ si vide | temps et mémoire $O(n)$ si vide | temps et mémoire $O(1)$ si vide |
| Ajoute un sommet $u$ | $O(n^2)$ (recopie) | $O(1)$ | $O(1)$ |
| Retire un sommet $u$ | $O(n^2)$ (recopie) | $O(d(u))$ si orienté, $O(n+m)$ sinon | $O(n)$ (suppression des arêtes) |
| Ajoute un arc $(u,v)$ | $O(1)$ | $O(d(u))$ si orienté, $O(d(u)+d(v))$ sinon | $O(1)$ (si liste d'arêtes) ou $O(1)$ en amorti (si ensemble d'arêtes) |
| Retire un arc $(u,v)$ | $O(1)$ | $O(d(u))$ si orienté, $O(d(u)+d(v))$ sinon | $O(n)$ (si liste d'arêtes) ou $O(1)$ en amorti (si ensemble d'arêtes) |
| Liste des sommets | $O(n)$ | $O(n)$ | $O(n)$ |
| Liste des arcs | $O(n^2)$ tout parcourir | $O(n)$ parcourir les $n$ listes de tailles $d(u)$, et $\sum_u d(u) = n$ | $O(1)$ (si liste d'arêtes) ou $O(n)$ (si ensemble d'arêtes) |
| Liste des voisins du nœud $u$ | $O(n)$ | $O(d(u))$ ($O(1)$ si on ne crée pas de nouvelle liste) | $O(n)$ |
| Degré du nœud $u$ | $O(n)$ | $O(n)$ | $O(n)$ |
| Liste des voisins sortant du nœud $u$ | $O(n)$ | $O(n)$ | $O(n)$ |
| Degré sortant du nœud $u$ | $O(n)$ | $O(n)$ | $O(n)$ |
| Liste des voisins entrant du nœud $u$ | $O(n)$ | $O(n)$ | $O(n)$ |
| Degré entrant du nœud $u$ | $O(n)$ | $O(n)$ | $O(n)$ |
In [62]:
try:
from tqdm import tqdm_notebook
except ImportError:
def tqdm_notebook(iterator, *args, **kwargs):
return iterator
In [64]:
def random_vertex(n):
return random.randint(0, n+1)
def random_edge(n):
return (random_vertex(n), random_vertex(n))
Un exemple¶
In [116]:
probability = 0.5
n = 1000
graph = randomGraph(AdjMatrixGraph, n=n, probability=probability)
%timeit graph.is_vertex(random_vertex(n))
%timeit graph.add_vertex(n + 5)
%timeit graph.add_edge(*random_edge(n))
%timeit graph.remove_edge(*random_edge(n))
%timeit graph.pred(random_vertex(n))
%timeit graph.is_pred(*random_edge(n))
%timeit graph.succ(random_vertex(n))
%timeit graph.is_succ(*random_edge(n))
%timeit graph.neighbors(random_vertex(n))
%timeit graph.is_neighbor(*random_edge(n))
Sans voir l'évolution en fonction de $n$, difficile de conclure quoi que ce soit de ces premières expériences…
Tests pour différentes tailles de graphes¶
On va stocker les temps de calculs dans une petite structure de la forme suivante, qui permettra d'afficher directement des courbes (le traitement est fait plus bas).
In [80]:
times = {
# clé sur n
"100": {
# clé sur p
r"|A| \simeq |S|": {
"AdjMatrixGraph": {
"operation1": 0.12,
# ...,
"operationN": 0.12,
},
"AdjListsGraph": {
"operation1": 0.12,
# ...,
"operationN": 0.12,
},
"EdgesListGraph": {
"operation1": 0.12,
# ...,
"operationN": 0.12,
},
},
},
}
In [117]:
import timeit
In [118]:
times = {}
for n in tqdm_notebook([100, 200, 400, 800, 1000, 1500, 2000, 2500, 3000, 3500, 4000, 4500, 5000], desc="n"):
number = 20 if n <= 200 else 5 # nb of repetitions of each operations
# print(f"\n\n For graphs with {n} vertexes:")
times[n] = {}
for probability, pname in tqdm_notebook([
(1.0/n, r"|A| \simeq |S|"), # p = 1/n => |A| ~= |S|
(1.0/np.sqrt(n), r"|A| \simeq |S|^{3/2}"), # p = 1/sqrt(n) => |A| ~= |S|^(3/2)
(0.1, r"|A| \simeq 0.1 |S|^2"), # p = 0.1 => |A| ~= 0.1 |S|^2
], desc="proba"):
times[n][pname] = {}
# print(f"\n and link probability of {probability}:")
for GraphClass in [AdjMatrixGraph, AdjListsGraph, EdgesListGraph]:
# print(f"\n for class {GraphClass}...")
graph = randomGraph(GraphClass, n=n, probability=probability)
the_times = {}
the_times["randomGraph"] = timeit.timeit(
"randomGraph(GraphClass, n=n, probability=probability)",
globals=globals(), number=number,
)
# print("Time to create a new graph:", the_times["randomGraph"])
the_times["is_vertex"] = timeit.timeit(
"graph.is_vertex(random_vertex(n))",
globals=globals(), number=number,
)
# print("Time to test presence of a vertex:", the_times["is_vertex"])
the_times["add_vertex"] = timeit.timeit(
"graph.add_vertex(n + 2)",
globals=globals(), number=number,
)
# print("Time to add the next vertex n + 2:", the_times["add_vertex"])
the_times["pred"] = timeit.timeit(
"graph.pred(random_vertex(n))",
globals=globals(), number=number,
)
# print("Time to compute pred:", the_times["pred"])
the_times["is_pred"] = timeit.timeit(
"graph.is_pred(*random_edge(n))",
globals=globals(), number=number,
)
# print("Time to test pred:", the_times["is_pred"])
the_times["succ"] = timeit.timeit(
"graph.succ(random_vertex(n))",
globals=globals(), number=number,
)
# print("Time to compute succ:", the_times["succ"])
the_times["is_succ"] = timeit.timeit(
"graph.is_succ(*random_edge(n))",
globals=globals(), number=number,
)
# print("Time to test succ:", the_times["is_succ"])
the_times["neighbors"] = timeit.timeit(
"graph.neighbors(random_vertex(n))",
globals=globals(), number=number,
)
# print("Time to compute neighbors:", the_times["neighbors"])
the_times["is_neighbor"] = timeit.timeit(
"graph.is_neighbor(*random_edge(n))",
globals=globals(), number=number,
)
# print("Time to test neighbors:", the_times["is_neighbor"])
the_times["add_edge"] = timeit.timeit(
"graph.add_edge(*random_edge(n))",
globals=globals(), number=number,
)
# print("Time to add an edge:", the_times["add_edge"])
times[n][pname][str(GraphClass)] = the_times
Afficher ces mesures de temps de complexités¶
In [103]:
import matplotlib.pyplot as plt
import seaborn as sns
sns.set(context="notebook", style="whitegrid", palette="hls", font="sans-serif", font_scale=1.1)
import matplotlib as mpl
mpl.rcParams['figure.figsize'] = (10, 7)
mpl.rcParams['figure.dpi'] = 120
Il faut écrire une fonction qui va extraire les données de ce times, et les afficher.
- J'ai choisi d'afficher une courbe différente pour chaque valeur de $p$, et de structure de données,
- Et sur chaque courbe, il y aura $n$ le nombre de sommets du graphe en abscisse, le temps (en milli secondes) en ordonnées, et des courbes pour chaque opérations.
In [193]:
def plotComplexitiesOfOperations(times):
values_n = list(times.keys())
values_p = list(times[values_n[0]].keys())
values_class = list(times[values_n[0]][values_p[0]].keys())
values_opname = list(times[values_n[0]][values_p[0]][values_class[0]].keys())
for class_name in values_class:
for pname in values_p:
data = {
n: times[n][pname][class_name]
for n in values_n
}
fig = plt.figure()
for opname in values_opname:
plt.semilogy(values_n, [ 1e6 * data[n][opname] for n in values_n ],
label=opname,
marker='o', lw=3, ms=12, alpha=0.7,
)
plt.xlabel("Values of $n$")
plt.ylabel("Measured time of operations (in milli-seconds)")
name = class_name.replace("<class '__main__.", "").replace("'>", "")
plt.title(f"For graphs with class {name}, and $p={pname}$")
plt.legend()
plt.show()
return fig
On vérifie cela :
In [194]:
_ = plotComplexitiesOfOperations(times)
Il faut écrire une fonction qui va extraire les données de ce times, et les afficher.
- J'ai choisi d'afficher une courbe différente pour chaque valeur de $p$, et de structure de données,
- Et sur chaque courbe, il y aura $n$ le nombre de sommets du graphe en abscisse, le temps (en milli secondes) en ordonnées, et des courbes pour chaque opérations.
In [195]:
def plotComplexitiesOfOperations2(times):
values_n = list(times.keys())
values_p = list(times[values_n[0]].keys())
values_class = list(times[values_n[0]][values_p[0]].keys())
values_opname = list(times[values_n[0]][values_p[0]][values_class[0]].keys())
for opname in values_opname:
for pname in values_p:
fig = plt.figure()
for class_name in values_class:
name = class_name.replace("<class '__main__.", "").replace("'>", "")
plt.plot(values_n, [ times[n][pname][class_name][opname] for n in values_n ],
label=name, marker='o',
lw=3, ms=12, alpha=0.8)
plt.xlabel("Values of $n$")
plt.ylabel("Measured time of operations (in seconds)")
plt.title(f"For the operation {opname}, and ${pname}$")
plt.legend()
plt.show()
return fig
On vérifie cela :
In [196]:
_ = plotComplexitiesOfOperations2(times)
Parcours en profondeur¶
On va simplement implémenter l'algorithme donné en cours, avec deux fonctions génériques post_visit et pre_visit.
Version récursive : vue en cours¶
Un exemple :
In [219]:
random.seed(12)
graph = randomGraph(AdjMatrixGraph, 10, 0.05, oriented=False)
In [220]:
plt.figure(figsize=(4, 3))
graph.draw()
Out[220]:
In [221]:
dfs_recursive(graph, 0)
Out[221]:
Ici on a pu vérifier que sur cet exemple de graphe, $0, 4, 5, 9, 6$ sont dans la même composante connexe.
Version itérative : pas vue en cours, avec une pile¶
In [228]:
def pre_visit(u):
print(f"Previsit of u = {u}")
In [229]:
def post_visit(u):
print(f"Postvisit of u = {u}")
In [230]:
def dfs_iterative(graph, start, seen=None):
""" DFS, detect connected component, iterative implementation.
- graph: directed graph (any of the class defined above)
- node: from where start graph exploration
- seen (bool array): will be set true for the connected component containing node.
- Complexity: O(|S|+|A|).
"""
if seen is None:
seen = [False for _ in range(graph.nb_vertexes)]
seen[start] = True
to_visit_next = [start]
while to_visit_next: # while stack is not empty
node = to_visit_next.pop() # head of the stack / tête de la pile, O(1)
pre_visit(node)
for neighbor in graph.neighbors(node):
if not seen[neighbor]:
seen[neighbor] = True
to_visit_next.append(neighbor) # add to the stack, O(1)
post_visit(node) # /!\ not the same order as for the recursive function!
return seen
Un exemple :
In [231]:
random.seed(12)
graph = randomGraph(AdjMatrixGraph, 10, 0.05, oriented=False)
In [234]:
plt.figure(figsize=(4, 3))
graph.draw()
Out[234]:
In [235]:
dfs_iterative(graph, 0)
Out[235]:
Ici on a pu vérifier que sur cet exemple de graphe, $0, 4, 5, 9, 6$ sont dans la même composante connexe.
Application : composantes connexes d'un graphe non orienté¶
In [261]:
def find_connected_components(graph):
""" Find all the connected components of a graph.
- graph: undirected graph (any of the class defined above)
- returns: list of vertices in a cycle, or None
- Complexity: O(|S|+|A|).
"""
n = graph.nb_vertexes
seen = [False for _ in range(n)]
# all nodes start by having their unique connected components
representants = [i for i in range(n)] # maps i to a representant of its connected components
start = -1
while not all(seen):
start += 1
if seen[start]:
continue
seen[start] = True
to_visit_next = [start]
while to_visit_next: # while stack is not empty
node = to_visit_next.pop() # head of the stack / tête de la pile, O(1)
for neighbor in graph.neighbors(node):
if not seen[neighbor]:
seen[neighbor] = True
representants[neighbor] = start
to_visit_next.append(neighbor) # add to the stack, O(1)
# now we can build the list of set of all connected components
list_of_connected_components = [
{ i for i in range(n) if representants[i] == representant }
for representant in set(representants)
]
return list_of_connected_components, representants
Un exemple :
In [262]:
random.seed(12)
graph = randomGraph(AdjMatrixGraph, 10, 0.05, oriented=False)
In [263]:
plt.figure(figsize=(4, 3))
graph.draw()
Out[263]:
In [264]:
find_connected_components(graph)
Out[264]:
Ici on a pu vérifier que sur cet exemple de graphe, $0, 4, 5, 9, 6$ sont dans la même composante connexe, que $1$ et $8$ sont isolés, et que $2, 3, 7$ sont dans une dernière composante connexe.
Application : trouver un cycle dans un graphe non orienté¶
In [269]:
def find_cycle(graph):
""" Find a cycle in an undirected graph
- graph: undirected graph (any of the class defined above)
- returns: list of vertices in a cycle, or None
- Complexity: O(|S|+|A|).
"""
n = graph.nb_vertexes
prec = [None] * n # ancestor marks for visited vertices
for u in range(n):
if prec[u] is None: # unvisited vertex
to_visit_next = [u] # start new DFS
prec[u] = u # mark root (not necessary for this algorithm)
while to_visit_next:
u = to_visit_next.pop()
for v in graph.neighbors(u): # for all neighbors
if v != prec[u]: # except arcs to father in DFS tree
if prec[v] is not None:
cycle = [v, u] # cycle found, (u,v) back edge
while u not in (prec[v], prec[u]): # directed
u = prec[u] # climb up the tree
cycle.append(u)
return cycle
else:
prec[v] = u # v is new vertex in tree
to_visit_next.append(v)
Un exemple :
In [270]:
random.seed(12)
graph = randomGraph(AdjMatrixGraph, 10, 0.05, oriented=False)
In [271]:
plt.figure(figsize=(4, 3))
graph.draw()
Out[271]:
In [272]:
find_cycle(graph)
Out[272]:
Ici on a pu vérifier que sur cet exemple de graphe, $[6, 9, 0]$ est bien un cycle.
In [282]:
random.seed(123)
graph = randomGraph(AdjMatrixGraph, 5, 0.05, oriented=False)
In [283]:
plt.figure(figsize=(4, 3))
graph.draw()
Out[283]:
In [284]:
find_cycle(graph)
Pas de cycle dans ce graphe qui est trop creux !
In [ ]:
In [198]:
def pre_visit(u, depth=0):
print(f"{' '*depth}Previsit of u = {u}")
In [199]:
def post_visit(u, depth=0):
print(f"{' '*depth}Postvisit of u = {u}")
In [218]:
def dfs_recursive(graph, node, seen=None, depth=0):
""" DFS, detect connected component, recursive implementation.
- graph: directed graph (any of the class defined above)
- node: from where start graph exploration
- seen (bool array): will be set true for the connected component containing node.
- Complexity: O(|S|+|A|).
"""
if seen is None:
seen = [False for _ in range(graph.nb_vertexes)]
if seen[node]:
return seen # nothing to do
seen[node] = True
pre_visit(node, depth=depth)
for neighbor in graph.neighbors(node):
if not seen[neighbor]:
dfs_recursive(graph, neighbor, seen=seen, depth=depth+1)
post_visit(node, depth=depth)
return seen
Un exemple :
In [219]:
random.seed(12)
graph = randomGraph(AdjMatrixGraph, 10, 0.05, oriented=False)
In [220]:
plt.figure(figsize=(4, 3))
graph.draw()
Out[220]:
In [221]:
dfs_recursive(graph, 0)
Out[221]:
Ici on a pu vérifier que sur cet exemple de graphe, $0, 4, 5, 9, 6$ sont dans la même composante connexe.
Parcours en largeur¶
On va simplement implémenter l'algorithme donné en cours, avec deux fonctions génériques post_visit et pre_visit.
On utilise une file implémentée naïvement avec un list de Python, mais on pourrait aussi utiliser la librairie standard de Python (queue.Queue).
In [286]:
def pre_visit(u):
print(f"Previsit of u = {u}")
In [287]:
def post_visit(u):
print(f"Postvisit of u = {u}")
In [288]:
def bfs_iterative(graph, start, seen=None):
""" DFS, iterative implementation.
- graph: directed graph (any of the class defined above)
- node: from where start graph exploration
- seen (bool array): will be set true for the connected component containing node.
- Complexity: O(|S|+|A|).
"""
if seen is None:
seen = [False for _ in range(graph.nb_vertexes)]
seen[start] = True
to_visit_next = [start]
while to_visit_next: # while queue is not empty
node = to_visit_next.pop() # head of the queue / tête de la file, O(1)
pre_visit(node)
for neighbor in graph.neighbors(node):
if not seen[neighbor]:
seen[neighbor] = True
to_visit_next.insert(0, neighbor) # add to the queue, O(1) if well done
post_visit(node) # /!\ not the same order as for the recursive function!
return seen
Un exemple :¶
In [290]:
random.seed(12)
graph = randomGraph(AdjMatrixGraph, 10, 0.05, oriented=False)
In [291]:
plt.figure(figsize=(4, 3))
graph.draw()
Out[291]:
In [292]:
bfs_iterative(graph, 0)
Out[292]:
On voit que $5$ a été visité en dernier, c'est bien différent du parcours en profondeur qui allait le visiter avant.
In [293]:
dfs_iterative(graph, 0)
Out[293]:
Distance des plus courts chemins avec un parcours en largeur¶
On suit l'algorithme vu en cours.
In [294]:
def bfs_iterative_shortest_paths(graph, start):
""" DFS, compute shortest paths, iterative implementation.
- graph: directed graph (any of the class defined above)
- node: from where start graph exploration
- seen (bool array): will be set true for the connected component containing node.
- Complexity: O(|S|+|A|).
"""
color = ["white" for _ in range(graph.nb_vertexes)]
parent = [None for _ in range(graph.nb_vertexes)]
distance = [float('+inf') for _ in range(graph.nb_vertexes)]
color[start] = "gray"
distance[start] = 0
to_visit_next = [start]
while to_visit_next: # while queue is not empty
node = to_visit_next.pop() # head of the queue / tête de la file, O(1)
for neighbor in graph.neighbors(node):
if color[neighbor] == "white":
color[neighbor] = "gray"
parent[neighbor] = node
distance[neighbor] = distance[node] + 1
to_visit_next.insert(0, neighbor) # add to the queue, O(1) if well done
color[node] = "black"
return color, parent, distance
In [295]:
bfs_iterative_shortest_paths(graph, 0)
Out[295]:
Algorithme de Dijkstra naïf¶
On utilise un tas binaire min pour maintenir la file de priorité, mais sans pouvoir modifier la priorité d'un élément (on le fait plus bas).
Le module heapq de la bibliothèque standard implémente les opérations d'ajout et d'extraction d'un tas binaire min (comme on l'a vu au CM2).
In [296]:
from heapq import heappop, heappush
In [303]:
def dijkstra(graph, weight, source=0, target=None):
""" Single source shortest paths by Dijkstra
- param graph: directed graph (any of the class defined above)
- param weight: in matrix format or same listdict graph
- assumes: weights are non-negative
- param source: source vertex
- param target: if given, stops once distance to target found
- returns: distance table, precedence table
- complexity: O(|S| + |A| log|A|)
"""
n = graph.nb_vertexes
assert all(weight[u][v] >= 0 for u in range(n) for v in graph.neighbors(u))
prec = [None] * n
black = [False] * n
dist = [float('inf')] * n
dist[source] = 0
heap = [(0, source)]
while heap:
dist_node, node = heappop(heap) # Closest node from source
if not black[node]:
black[node] = True
if node == target:
break
for neighbor in graph.neighbors(node):
dist_neighbor = dist_node + weight[node][neighbor]
if dist_neighbor < dist[neighbor]:
dist[neighbor] = dist_neighbor
prec[neighbor] = node
heappush(heap, (dist_neighbor, neighbor))
return dist, prec
Exemple :
In [304]:
random.seed(12)
graph = randomGraph(AdjMatrixGraph, 10, 0.05, oriented=False)
In [307]:
plt.figure(figsize=(4, 3))
graph.draw()
Out[307]:
Avec des poids égaux à 1 on retrouve ce que calculait le parcours en largeur :
In [311]:
weight = np.zeros((10, 10), dtype=int)
for (u, v) in graph.edges:
weight[u, v] = 1
In [312]:
weight
Out[312]:
In [313]:
dijkstra(graph, weight, source=0, target=None)
Out[313]:
Mais avec des distances non triviales, le chemin optimal peut être différent.
In [341]:
weight = np.zeros((10, 10), dtype=int)
for (u, v) in graph.edges:
weight[u, v] = 1 + 10*(v < 6 and u < 6)
In [342]:
weight
Out[342]:
In [343]:
dijkstra(graph, weight, source=0, target=None)
Out[343]:
On voit que le chemin optimal pour aller de 0 à 6 n'est pas l'arc direct $0 \to 6$, de poids $11$, mais $0 \to 9 \to 6$ de poids $1 + 1 = 2$.
File de priorité min : implémentation maison¶
Le fait d'implémenter intelligement la méthode update ci dessous permet d'avoir un algorithme de Dijkstra qui soit efficace.
In [352]:
class OurHeap:
""" min heap
* heap: is the actual heap, heap[1] = index of the smallest element
* rank: inverse of heap with rank[x]=i iff heap[i]=x
* n: size of the heap
:complexity: init O(n log n), len O(1),
other operations O(log n) in expectation
and O(n) in worst case, due to the usage of a dictionary
"""
def __init__(self, items):
self.heap = [None] # index 0 will be ignored
self.rank = {}
for x in items:
self.push(x)
def __len__(self):
return len(self.heap) - 1
def push(self, x):
"""Insert new element x in the heap.
Assumption: x is not already in the heap"""
assert x not in self.rank
i = len(self.heap)
self.heap.append(x) # add a new leaf
self.rank[x] = i
self.up(i) # maintain heap order
def pop(self):
"""Remove and return smallest element"""
root = self.heap[1]
del self.rank[root]
x = self.heap.pop() # remove last leaf
if self: # if heap is not empty
self.heap[1] = x # put last leaf to root
self.rank[x] = 1
self.down(1) # maintain heap order
return root
def up(self, i):
"""The value of heap[i] has decreased. Maintain heap invariant."""
x = self.heap[i]
while i > 1 and x < self.heap[i // 2]:
self.heap[i] = self.heap[i // 2]
self.rank[self.heap[i // 2]] = i
i //= 2
self.heap[i] = x # insertion index found
self.rank[x] = i
def down(self, i):
"""the value of heap[i] has increased. Maintain heap invariant."""
x = self.heap[i]
n = len(self.heap)
while True:
left = 2 * i # climb down the tree
right = left + 1
if (right < n and self.heap[right] < x and
self.heap[right] < self.heap[left]):
self.heap[i] = self.heap[right]
self.rank[self.heap[right]] = i # go back up right child
i = right
elif left < n and self.heap[left] < x:
self.heap[i] = self.heap[left]
self.rank[self.heap[left]] = i # go back up left child
i = left
else:
self.heap[i] = x # insertion index found
self.rank[x] = i
return
def update(self, old, new):
"""Replace an element in the heap
"""
i = self.rank[old] # change value at index i
del self.rank[old]
self.heap[i] = new
self.rank[new] = i
if old < new: # maintain heap order
self.down(i)
else:
self.up(i)
Algorithme de Dijkstra¶
In [353]:
def dijkstra_update_heap(graph, weight, source=0, target=None):
""" Single source shortest paths by Dijkstra
with a heap implementing item updates
- param graph: directed graph (any of the class defined above)
- param weight: in matrix format or same listdict graph
- assumes: weights are non-negative
- param source: source vertex
- param target: if given, stops once distance to target found
- returns: distance table, precedence table
- complexity: O(|S| + |A| log|A|)
"""
n = graph.nb_vertexes
assert all(weight[u][v] >= 0 for u in range(n) for v in graph.neighbors(u))
prec = [None] * n
dist = [float('inf')] * n
dist[source] = 0
heap = OurHeap([(dist[node], node) for node in range(n)])
while heap:
dist_node, node = heap.pop() # Closest node from source
if node == target:
break
for neighbor in graph.neighbors(node):
old = dist[neighbor]
new = dist_node + weight[node][neighbor]
if new < old:
dist[neighbor] = new
prec[neighbor] = node
heap.update((old, neighbor), (new, neighbor))
return dist, prec
Exemple :
In [354]:
random.seed(12)
graph = randomGraph(AdjMatrixGraph, 10, 0.05, oriented=False)
In [355]:
plt.figure(figsize=(4, 3))
graph.draw()
Out[355]:
Avec des poids égaux à 1 on retrouve ce que calculait le parcours en largeur :
In [356]:
weight = np.zeros((10, 10), dtype=int)
for (u, v) in graph.edges:
weight[u, v] = 1
In [357]:
dijkstra_update_heap(graph, weight, source=0, target=None)
Out[357]:
Mais avec des distances non triviales, le chemin optimal peut être différent.
In [358]:
weight = np.zeros((10, 10), dtype=int)
for (u, v) in graph.edges:
weight[u, v] = 1 + 10*(v < 6 and u < 6)
In [359]:
weight
Out[359]:
In [360]:
dijkstra_update_heap(graph, weight, source=0, target=None)
Out[360]:
Algorithme A*¶
Je ne vais pas prendre le temps de l'implémenter. Allez regarder un des liens suivants, si vous avez envie :
- https://fr.wikipedia.org/wiki/Algorithme_A*
- https://www.redblobgames.com/pathfinding/a-star/implementation.html
D'autres :