#!/usr/bin/env python
# coding: utf-8
# # Table of Contents
#
# # [ALGO1 : Introduction à l'algorithmique](https://perso.crans.org/besson/teach/info1_algo1_2019/)
#
# - [Page du cours](https://perso.crans.org/besson/teach/info1_algo1_2019/) : https://perso.crans.org/besson/teach/info1_algo1_2019/
# - Magistère d'Informatique de Rennes - ENS Rennes - Année 2019/2020
# - Intervenants :
# + Cours : [Lilian Besson](https://perso.crans.org/besson/)
# + Travaux dirigés : [Raphaël Truffet](http://perso.eleves.ens-rennes.fr/people/Raphael.Truffet/)
# - Références :
# + [Open Data Structures](http://opendatastructures.org/ods-python.pdf)
# # Cours Magistral 2
# ## Structures de données pour représenter un ensemble de valeurs distinctes
#
# - Après avoir étudié comment représenter $$ une *séquence ordonnée* de valeurs $a_i$ dans un domaine $D$ (e.g., des entiers), on s'intéresse aujourd'hui à représenter un *ensemble non ordonné* de valeurs : $\{a_1,\dots,a_n\}$.
# - On va utiliser des valeurs entières, par concision : $D=\mathbb{N}$, `d = int`.
# ## Type abstrait
# - On fixe $D$ le domaine de nos valeurs, et `d` leur type.
# - On définit `Set` le type abstrait des ensembles (collections non ordonnés) de valeurs de type `d`.
#
# On veut les opérations suivantes :
#
# newEmptySet : () -> Set // créer un ensemble vide
# len : Set -> int // donner le nombre d'éléments de cet ensemble
# contains : Set * d -> bool // tester l'appartenance
# add : Set * d -> Set // ajouter un élément à cet ensemble
# pop : Set * d -> Set // retirer un élément à cet ensemble (s'il est présent)
# values : Set -> List // retourne la liste de valeurs présentes dans l'ensemble
# On peut aussi vouloir les opérations suivantes, qui peuvent toutes s'implémenter avec les primitives ci-dessus :
#
# isEmpty : Set -> bool // test si l'ensemble est vide
# copy : Set -> Set // copie l'ensemble
#
# On peut aussi vouloir les opérations entre ensembles suivantes, qui peuvent toutes s'implémenter avec les primitives ci-dessus :
#
# union : Set * Set -> Set
# // contient les éléments présents dans au moins un des deux ensembles
#
# intersection : Set * Set -> Set
# // contient les éléments présents dans les deux ensembles
#
# difference : Set * Set -> Set
# // contient les éléments présents dans le premier mais pas le deuxième ensemble
#
# symmetric_difference : Set * Set -> Set
# // contient les éléments présents dans le premier mais pas le deuxième ensemble ou dans le deuxième mais pas le premier (xor)
#
# issubset : Set * Set -> bool
# // test si le premier ensemble est contenu dans le second
#
# issuperset : Set * Set -> bool
# // test si le premier ensemble est contenu dans le second
# ----
# ## Implémentation des opérations non primitives à partir des opérations primitives
# - Avec OCaml, on pourrait écrire un foncteur.
# - Avec Python, on va écrire une classe, et on pourra obtenir différentes implémentations complètes de la structure de données d'ensemble, à partir de différentes implémentations partielles des opérations primitives. C'est assez naïf : le code est indépendant de l'implémentation sous jacente de `add`/`pop` et de l'itérations :
# In[1]:
class SetIterator():
def __init__(self, a_set):
self.values = a_set.values()
self.maxcurrent = len(a_set)
self.current = 0
def __iter__(self):
return self
def __next__(self):
if self.current >= self.maxcurrent:
raise StopIteration
else:
self.current += 1
return self.values[self.current - 1]
# In[2]:
class SetWithNonPrimOperations():
def isEmpty(self):
return len(self) == 0
def __iter__(self):
return SetIterator(self)
def copy(self):
""" A new set containing the same values."""
new_set = self.__class__()
for value in self:
new_set.add(value)
return new_set
def difference(self, other_set):
""" A new set containing the values in self but not other_set."""
new_set = self.__class__()
for value in self:
if value not in other_set:
new_set.add(value)
return new_set
def symmetric_difference(self, other_set):
""" A new set containing the values in self but not other_set and the values in other_set but not self (XOR)."""
new_set = self.__class__()
for value in self:
if value not in other_set:
new_set.add(value)
for value in other_set:
if value not in self:
new_set.add(value)
return new_set
def intersection(self, other_set):
""" A new set containing the values in self and in other_set."""
new_set = self.__class__()
for value in self:
if value in other_set:
new_set.add(value)
return new_set
def union(self, other_set):
""" A new set containing the values in self or in other_set."""
new_set = self.__class__()
for value in self:
new_set.add(value)
for value in other_set:
new_set.add(value)
return new_set
def isdisjoint(self, other_set):
""" True if all the values in self are not in other_set."""
for value in self:
if value in other_set:
return False
return True
def issubset(self, other_set):
""" True if all the values in self are in other_set."""
for value in self:
if value not in other_set:
return False
return True
def issuperset(self, other_set):
""" True if all the values in other_set are in self."""
for value in other_set:
if value not in self:
return False
return True
def clear(self):
""" Remove (pop) all the values in self."""
for value in self:
self.pop(value)
def remove(self, value):
self.pop(value)
def __contains__(self, value):
return self.contains(value)
def __str__(self):
""" Represent the values of the set in a string {a1,...,an}."""
str_list = str(self.values())
return "{" + str_list.strip("[]") + "}"
# ----
# ## Tests communs aux différentes implémentations
#
# On écrit un petit test qui sera utilisé avec les différentes implémentations.
# In[3]:
def un_petit_test_avec_une_structure_densemble(SetClass):
ens = SetClass()
print(ens)
assert not ens
for x in range(10):
assert x not in ens
ens.add(x)
assert x in ens
print(ens)
# ens = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}
assert ens
assert str(ens) == "{0, 1, 2, 3, 4, 5, 6, 7, 8, 9}"
print("S1 =", ens)
for x in range(20, 30):
assert x not in ens
ens2 = SetClass()
print(ens2)
for x in range(5, 10):
assert x not in ens2
ens2.add(x)
assert x in ens2
print(ens2)
# ens2 = {5, 6, 7, 8, 9}
assert str(ens2) == "{5, 6, 7, 8, 9}"
print("S2 =", ens2)
assert ens2.issubset(ens)
assert ens.issuperset(ens2)
assert [v for v in ens.intersection(ens2)] == [v for v in ens2]
assert [v for v in ens.intersection(ens2)] == [5, 6, 7, 8, 9]
assert [v for v in ens.difference(ens2)] == [0, 1, 2, 3, 4]
ens3 = SetClass()
print(ens3)
for x in range(20, 25):
assert x not in ens3
ens3.add(x)
assert x in ens3
print(ens3)
assert len(ens3) == 5
for x in range(20, 25):
ens3.add(x)
assert x in ens3
print(ens3)
assert len(ens3) == 5
# ens3 = {20, 21, 22, 23, 24}
assert str(ens3) == "{20, 21, 22, 23, 24}"
print("S3 =", ens3)
assert not ens.issubset(ens3)
assert not ens.issuperset(ens3)
assert not ens3.issubset(ens)
assert not ens3.issuperset(ens)
assert not ens3.intersection(ens)
assert not ens.intersection(ens3)
print("S1 union S2 =", ens.union(ens2), " = S2 union S1 =", ens2.union(ens))
print("S1 union S3 =", ens.union(ens3))
print("S2 union S3 =", ens2.union(ens3))
print("S1 inter S2 =", ens.intersection(ens2), " != S2 inter S1 =", ens2.intersection(ens))
print("S1 inter S3 =", ens.intersection(ens3), " != S3 inter S1 =", ens3.intersection(ens))
print("S2 inter S3 =", ens2.intersection(ens3), " != S3 inter S2 =", ens3.intersection(ens2))
print("S1 diff S2 =", ens.difference(ens2), " != S2 diff S1 =", ens2.difference(ens))
print("S1 diff S3 =", ens.difference(ens3), " != S3 diff S1 =", ens3.difference(ens))
print("S2 diff S3 =", ens2.difference(ens3), " != S3 diff S2 =", ens3.difference(ens2))
print("S1 diff sym S2 =", ens.symmetric_difference(ens2), " != S2 diff sym S1 =", ens2.symmetric_difference(ens))
print("S1 diff sym S3 =", ens.symmetric_difference(ens3), " != S3 diff sym S1 =", ens3.symmetric_difference(ens))
print("S2 diff sym S3 =", ens2.symmetric_difference(ens3), " != S3 diff sym S2 =", ens3.symmetric_difference(ens2))
# Le deuxième test va juste être une suite d'ajout et de suppression de valeurs dans l'ensemble.
#
# Il servira pour mesurer l'efficacité temporelle des deux opérations de bases (`add`/`pop`), en fonction de l'amplitude des valeurs de l'ensemble (`max_value`/`min_value`), et de la taille de l'ensemble qui sera construit (`size`).
# In[4]:
import random
def random_add_remove_test(SetClass, size=1000, max_value=10_000, min_value=-10_000):
ens = SetClass()
for _ in range(size):
x = random.randint(min_value, max_value)
ens.add(x)
assert x in ens
values = ens.values()
for _ in range(size):
x = random.choice(values)
if random.random() <= 0.5:
ens.add(x)
assert x in ens
else:
if x in ens:
ens.remove(x)
assert x not in ens
# ## Implémentation naïve avec une structure linéaire (liste, tableau etc)
# - On utilise une liste ou un tableau (en Python, `list`) pour stocker les valeurs.
# - Voyons les implémentations concrètes (les complexités sont discutées pour chacune plus bas).
# In[5]:
class SetWithList(SetWithNonPrimOperations):
def __init__(self):
self._values = []
def __len__(self):
""" Return n the current size of the set."""
return len(self._values)
def contains(self, value):
""" Test if value is in the set.
- Test linearly the equality with all values in the list.
- Takes O(n) time in worst case."""
for other_value in self._values:
if other_value == value:
return True
return False
# equivalent to
# return value in self._values
def add(self, value):
""" Add value in the set if it is not present.
- Takes O(n) time in worst case."""
if value not in self:
self._values.append(value)
def pop(self, value):
""" Remove value in the set if it is present.
- Takes O(n) time in worst case."""
if value in self: # O(n)
location = self._values.index(value) # O(n), but happens only once
del self._values[location] # O(n)
def values(self):
""" Return a fresh list of the values of the set (not the actual list, to protect it).
- Takes O(n) time in worst case."""
return list(self._values)
# On teste cette première structure :
# In[6]:
un_petit_test_avec_une_structure_densemble(SetWithList)
# - On pourrait faire pareil avec n'importe quelle structure linéaire : liste simplement ou doublement chaînée, tableau dynamique (ce qu'on a fait avec `list` de Python), file/pile d'attente, etc.
#
# - Le bilan des complexités des opérations est le suivant (si $n=\texttt{len}(S_1)$ et $m=\texttt{len}(S_2)$) :
#
# | Opérations | Complexité pire cas | Complexité moyenne* |
# |------------|------------|------------|
# | `newEmptySet()` | $O(1)$ | $O(1)$ |
# | `len(S1)` | $O(n)$ | $O(n)$ |
# | `contains(S1, x)` | $O(n)$ | $O(n)$ |
# | `add(S1, x)` | $O(n)$ | $O(n)$ |
# | `pop(S1, x)` | $O(n)$ | $O(n)$ |
# | `values(S1)` | $O(n)$ | $O(n)$ |
# | `isEmpty(S1)` | $O(n)$ | $O(n)$ |
# | `copy(S1)` | $O(n)$ | $O(n)$ |
# | `union(S1, S2)` | $O(n + m)$ | $O(n + m)$ |
# | `intersection(S1, S2)` | $O(n + m)$ | $O(n + m)$ |
# | `difference(S1, S2)` | $O(n + m)$ | $O(n + m)$ |
# | `symmetric_difference(S1, S2)` | $O(n + m)$ | $O(n + m)$ |
# | `issubset(S1, S2)` | $O(n + m)$ | $O(n + m)$ |
# | `issuperset(S1, S2)` | $O(n + m)$ | $O(n + m)$ |
#
# > Il reste à définir ce que signifie complexité moyenne. Regardez par exemple dans [Introduction à l'Algorithmique, de Cormen et al].
# In[7]:
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithList, size=100, max_value=100)')
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithList, size=100, max_value=1000)')
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithList, size=100, max_value=100000)')
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithList, size=100, max_value=10000000)')
# In[8]:
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithList, size=1000, max_value=100)')
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithList, size=1000, max_value=1000)')
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithList, size=1000, max_value=100000)')
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithList, size=1000, max_value=10000000)')
# In[9]:
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithList, size=10000, max_value=100)')
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithList, size=10000, max_value=1000)')
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithList, size=10000, max_value=100000)')
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithList, size=10000, max_value=10000000)')
# Plus `max_value` est grande, plus il y a de valeurs différentes, donc plus on a une liste qui sera longue, et donc plus les opérations coûtent cher.
# ----
# ## Implémentation native avec `set` en Python
# In[10]:
class NativeSet(set, SetWithNonPrimOperations):
def values(self):
return list(self)
# et c'est tout
# In[11]:
un_petit_test_avec_une_structure_densemble(NativeSet)
# - Le bilan des complexités des opérations est le suivant (si $n=\texttt{len}(S_1)$ et $m=\texttt{len}(S_2)$) :
#
# | Opérations | Complexité pire cas | Complexité moyenne* |
# |------------|------------|------------|
# | `newEmptySet()` | $O(1)$ | $O(1)$ |
# | `len(S1)` | $O(1)$ | $O(1)$ |
# | `contains(S1, x)` | $O(n)$ | $O(1)$ 🎉 |
# | `add(S1, x)` | $O(n)$ | $O(1)$ 🎉 |
# | `pop(S1, x)` | $O(n)$ | $O(1)$ 🎉 |
# | `values(S1)` | $O(n)$ | $O(n)$ |
# | `isEmpty(S1)` | $O(1)$ | $O(1)$ |
# | `copy(S1)` | $O(n)$ | $O(n)$ |
# | `union(S1, S2)` | $O(n + m)$ | $O(n + m)$ |
# | `intersection(S1, S2)` | $O(n m)$ | $O(\min(n, m))$ 🎉 |
# | `difference(S1, S2)` | $O(n + m)$ | $O(n + m)$ |
# | `symmetric_difference(S1, S2)` | $O(n m)$ | $O(\max(n, m))$ |
# | `issubset(S1, S2)` | $O(n m)$ | $O(\min(n, m)))$ 🎉 |
# | `issuperset(S1, S2)` | $O(n m)$ | $O(\min(n, m)))$ 🎉 |
#
# > Référence : https://stackoverflow.com/questions/3949310/ddg#3949350, https://hg.python.org/releasing/3.6/file/tip/Objects/setobject.c et https://wiki.python.org/moin/TimeComplexity#set
# In[12]:
get_ipython().run_line_magic('timeit', 'random_add_remove_test(NativeSet, size=100, max_value=100)')
get_ipython().run_line_magic('timeit', 'random_add_remove_test(NativeSet, size=100, max_value=1000)')
get_ipython().run_line_magic('timeit', 'random_add_remove_test(NativeSet, size=100, max_value=1000_000)')
get_ipython().run_line_magic('timeit', 'random_add_remove_test(NativeSet, size=100, max_value=1000_000_000)')
# In[13]:
get_ipython().run_line_magic('timeit', 'random_add_remove_test(NativeSet, size=1000, max_value=100)')
get_ipython().run_line_magic('timeit', 'random_add_remove_test(NativeSet, size=1000, max_value=1000)')
get_ipython().run_line_magic('timeit', 'random_add_remove_test(NativeSet, size=1000, max_value=1000_000)')
get_ipython().run_line_magic('timeit', 'random_add_remove_test(NativeSet, size=1000, max_value=1000_000_000)')
# In[14]:
get_ipython().run_line_magic('timeit', 'random_add_remove_test(NativeSet, size=10_000, max_value=100)')
get_ipython().run_line_magic('timeit', 'random_add_remove_test(NativeSet, size=10_000, max_value=1000)')
get_ipython().run_line_magic('timeit', 'random_add_remove_test(NativeSet, size=10_000, max_value=1000_000)')
get_ipython().run_line_magic('timeit', 'random_add_remove_test(NativeSet, size=10_000, max_value=1000_000_000)')
# In[15]:
get_ipython().run_line_magic('timeit', 'random_add_remove_test(NativeSet, size=100_000, max_value=100)')
get_ipython().run_line_magic('timeit', 'random_add_remove_test(NativeSet, size=100_000, max_value=1000)')
get_ipython().run_line_magic('timeit', 'random_add_remove_test(NativeSet, size=100_000, max_value=1000_000)')
get_ipython().run_line_magic('timeit', 'random_add_remove_test(NativeSet, size=100_000, max_value=1000_000_000)')
# In[16]:
get_ipython().run_line_magic('timeit', 'random_add_remove_test(NativeSet, size=1000_000, max_value=100)')
get_ipython().run_line_magic('timeit', 'random_add_remove_test(NativeSet, size=1000_000, max_value=1000)')
get_ipython().run_line_magic('timeit', 'random_add_remove_test(NativeSet, size=1000_000, max_value=1000_000)')
get_ipython().run_line_magic('timeit', 'random_add_remove_test(NativeSet, size=1000_000, max_value=1000_000_000)')
# - On semble vérifier que l'implémentation native de Python est quasiment indépendante des valeurs stockées, dès qu'elles sont assez grandes.
# - Et que les complexités (amorties) des opérations `add`/`remove` sont quasiment indépendantes en la taille de l'ensemble ! (multiplier la taille $n$ par 10 multiplie presque le temps de calcul des $n$ opérations par 10). En fait, on voit qu'elles sont sous linéaires, mais pas constantes.
# ----
# ## Bidouillage 1/1 : implémentation avec des entiers 32/64 bits
#
# - Si on sait que les valeurs qu'on va ajouter dans nos ensembles sont comprises entre 0 et 31, on peut représenter un (petit) ensemble avec *un seul* entier 32 bits : si le $i$ème bit est à 1, c'est que $i$ est dans l'ensemble.
# - On peut faire pareil avec 64 bits.
# - En Python, les entiers sont à précision arbitraire, mais on peut utiliser `np.int32` pour avoir des entiers 32 bits natifs :
# In[17]:
import numpy as np
# - On va voir comment utiliser les opérations bit à bit pour réaliser les opérations sur les ensembles. [Documentation ?](https://docs.scipy.org/doc/numpy/reference/routines.bitwise.html)
# In[18]:
bin(0b0) # set {}
bin(0b1) # set {0}
bin(0b10) # set {1}
bin(0b11) # set {0, 1}
bin(np.bitwise_and(0b11, 0b01)) # {0, 1} inter {1} = {1}
bin(0b11 & 0b01) # {0, 1} inter {1} = {1}
bin(np.bitwise_or(0b01, 0b10)) # {0} union {1} = {0, 1}
bin(0b01 | 0b10) # {0} union {1} = {0, 1}
bin(np.bitwise_xor(0b11, 0b10)) # {0, 1} /\ {1} = {0} (symmetric difference)
bin(0b11 ^ 0b10) # {0, 1} /\ {1} = {0} (symmetric difference)
bin(np.bitwise_xor(0b101, 0b10)) # {0, 2} /\ {1} = {0, 1, 2} (symmetric difference)
bin(0b101 ^ 0b10) # {0, 2} /\ {1} = {0, 1, 2} (symmetric difference)
bin(np.left_shift(1, 0)) # = {0}
bin(1 << 0) # = {0}
bin(np.left_shift(1, 1)) # = {1}
bin(1 << 1) # = {1}
bin(np.left_shift(1, 7)) # = {7}
bin(1 << 7) # = {7}
# Et voilà la classe
# In[19]:
from math import log2
# In[57]:
class SetWithInt(SetWithNonPrimOperations):
def __init__(self, zero=0):
""" Use zero=0 to use native int, zero=np.int32(0) or np.int64(0) to use 32/64 bits."""
self.int = zero
def __len__(self):
""" Return n the current size of the set."""
return len(self.values())
def contains(self, value):
""" Test if value is in the set.
- Test one bit.
- This & means "bitwise and".
"""
return (self.int & (1 << value)) != 0
def add(self, value):
""" Add value in the set if it is not present.
- This |= means x = x | y and | is the "bitwise or" operation."""
self.int |= (1 << value)
def pop(self, value):
""" Remove value in the set if it is present.
- This ^= means x = x ^ y and | is the "bitwise xor" operation."""
self.int ^= (1 << value)
def values(self):
""" Return a fresh list of the values of the set.
- Takes O(n) time in worst case."""
if self.int == 0:
return []
else:
n = 1 + int(log2(self.int))
return [ i for i in range(n) if i in self]
# In[21]:
SetWithInt32 = lambda: SetWithInt(np.int32(0))
SetWithInt64 = lambda: SetWithInt(np.int64(0))
# On test :
# In[22]:
un_petit_test_avec_une_structure_densemble(SetWithInt32)
# Parler de complexité n'aura pas de sens ici : on s'autorise seulement des ensembles ayant jusqu'à 32 valeurs.
# Donc $n\leq32$, alors que les notations $O(n)$ (etc) sont des **notations asymptotiques** (ie. valables quand $n\to\infty$ !).
# ## Bidouillage 2/2 : implémentation avec des entiers en précision infinie avec Python
# - On ne verrait la différence que si on faisait des tests de la rapidité des opérations de bases, avec des valeurs $\leq 31$ en comparaison de la structure utilisant des entiers natifs sur 32 bits.
# - On voit aussi la différence quant au fait que les ensembles représentés avec des entiers natifs 32/64 bits ne peuvent stocker que des valeurs entre 0 et 31 ou 63.
# In[23]:
SetWithIntInfinite = lambda: SetWithInt(int(0))
# In[24]:
un_petit_test_avec_une_structure_densemble(SetWithIntInfinite)
# In[25]:
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithIntInfinite, size=1000, max_value=100, min_value=0)')
# In[26]:
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithIntInfinite, size=1000, max_value=1000, min_value=0)')
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithIntInfinite, size=1000, max_value=10000, min_value=0)')
# In[27]:
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithIntInfinite, size=1000_000, max_value=1000, min_value=0)')
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithIntInfinite, size=1000_000, max_value=10000, min_value=0)')
# Avec cet implémentation, on ne peut raisonnablement pas stocker des valeurs trop grandes.
# ----
# ## Implémentation avec des tables de hachage ?
#
# ### En Python : `set` ~= `dict` avec des valeurs "inutiles"
# L'implémentation standard des ensembles en Python, `set`, utilise en fait une implémentation très proche des `dict` de Python, avec des valeurs vides (et quelques optimisations).
# On va d'abord décrire le fonctionnement de tables de hachage simples, ne stockant que des valeurs (en fait, les clés des dictionnaires `dict`), et à la fin on expliquera rapidement comment généraliser au stockage de couples `(cle, valeur)`.
#
# ### Présentation de l'idée :
#
# - On suppose que les valeurs que l'on va stocker dans l'ensemble sont dans un domaine $D$. Par exemple, $D = \{0, \dots, 1023\}$.
# - On va se donner une fonction $f : D \to \{0, \dots, m\}$, qui soit simple à calculer. Par exemple, $m = 10$ et $f(x) = x \mod 10 \in\{0,\dots,9\}$.
# - La table de hachage va consister en un premier tableau, de taille $m$, qui en position $i$ va pointer vers une autre structure d'ensemble (e.g., une structure linéaire ou même une autre table de hachage, dans le cas du hachage chaîné). Cette structure d'ensemble va servir à stocker toutes les valeurs qui ont pour image $i$ par la fonction $f$.
#
# 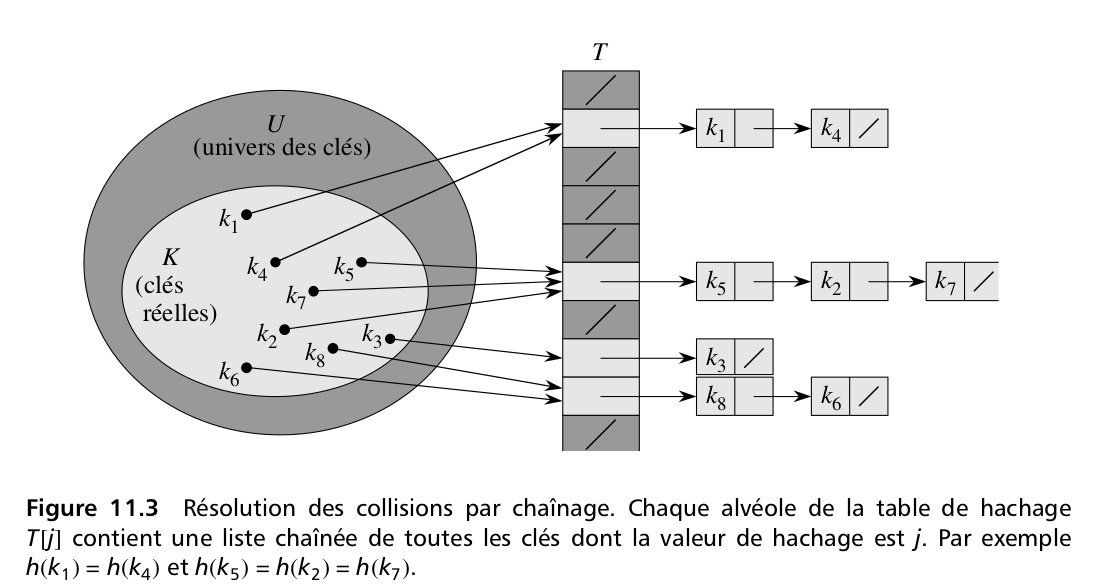 #
# Les opérations de base sur l'ensemble représenté par la table seront réalisées comme suit :
#
# - Lorsqu'on ajoute une valeur $v$ à la table :
# + on calcule $j = f(v)$,
# + on ajoute $v$ à l'ensemble en position $j$ du tableau :
# * si c'est une liste chaînée par exemple, on créée une nouvelle liste contenant $v$ ou on ajoute $v$ à la fin de la liste chaînée,
# * si c'est une autre table de hachage, on l'ajoute en utilisant la primitive de la table,
# * etc
#
# - Lorsque l'on veut tester l'appartenance de $v$ à la table :
# + on calcule $j = f(v)$ (le numéro de la cellule contenant $v$, on parle parfois aussi d'alvéole),
# + on test si $v$ appartient à la liste / l'ensemble stocké en position $j$ du tableau.
#
# - La suppression fonctionne comme l'ajout.
# ### Comment stocker les plus petits ensembles ?
# - A première vue, on est face à une idée stupide : pour stocker un ensemble, on en stocke $m$…
# - Mais si la fonction de hachage est bien faite, si elle envoie les données $x \in D$ sur les $m$ différentes valeurs uniformément (en gros si $\forall j\in\{0,\dots,m\}, \# \{ x \in D : f(x) = j\} \simeq \frac{1}{m}$)
# - Les opérations de base sur les sous ensembles (les alvéoles) sont en complexités (au pire cas) linéaires dans la taille de ces sous ensembles, ce qui dépend du remplissage actuel de la table.
# Par exemple, avec $m = 20$, la fonction $f(x) = x \mod 20$ et des valeurs qui sont des entiers aléatoirement tirés (cf. [cette page de démonstration](http://people.irisa.fr/Francois.Schwarzentruber/hash_tables_demo/)) :
#
# 0 |_| --> []
# 1 |_| --> [98281,92581,11221]
# 2 |_| --> [91422,84022,65742,55322,59162]
# 3 |_| --> [64583,43563]
# 4 |_| --> []
# 5 |_| --> [1665,1585]
# 6 |_| --> [80986,80446,95966,28446,74726]
# 7 |_| --> [40867,86987,47907]
# 8 |_| --> [86268,31908,21688,59068,50448]
# 9 |_| --> [65989,38369,69769]
# 10 |_| --> [8670]
# 11 |_| --> [27211,99291]
# 12 |_| --> [43532]
# 13 |_| --> [55033,3873,76353]
# 14 |_| --> [74734]
# 15 |_| --> [36075,62495,42015,75435,26415]
# 16 |_| --> [85336,21856,18376,46436,64516]
# 17 |_| --> [66117,95857]
# 18 |_| --> [76438]
# 19 |_| --> []
#
# Par exemples :
# - Ici, chercher l'appartenance de 76438 à l'ensemble se fera en deux opérations : calculer $f(76438)=18$, puis en cherchant (en une seule opération) $76438$ dans `T[18]=` $[76438]$.
# - Chercher $59068$ va trouver la cellule $f(59068) = 8$, qui contient 5 valeurs, et donc trouver $59068$ dans la liste $[86268,31908,21688,59068,50448]$ prend quatre opérations.
# ### Choix de la fonction de hachage
# - Il existe plein de fonction de hachage pour différentes utilisations.
# - Pour des entiers, on peut prendre $f(x) = x \mod m$ et adapter $m$ en fonction des propriétés voulues par notre structure.
# + Plus $m$ est grand, plus les opérations seront rapides mais plus on consomme de mémoire, inversement un plus petit $m$ réduit l'impact mémoire mais augmente l'impact temps.
# + En fait, si nos entiers sont entre $0$ et $M$, on peut avoir les deux cas extrêmes suivants :
# * la pire solution vis à vis du temps de calcul est d'utiliser $m = 1$, tous les entiers sont stockés dans la même liste. On a donc une complexité en $O(n)$ pour les opérations de base, cf. plus haut.
# * la meilleure solution vis à vis du temps de calcul est d'utiliser $m = M$, ie. la table de hachage est juste un vecteur de bit, où la case $j$ vaut $T[j]=[j]$ ssi $j$ est dans la table. Chaque entier est stocké dans sa propre liste, de taille vide ou de taille 1. On a donc une complexité en $O(1)$ pour les opérations de base, cf. plus haut.
# * choisir un $m$ intermédiaire, par exemple $m = O(\log(M))$, peut permettre de balancer entre les deux extrêmes.
#
# - Pour des chaînes de caractères, on peut faire la somme des hachés de chaque caractères, modulo un certain nombre, ou n'importe quelle idée de ce genre.
#
# - Python utilise la fonction `hash()` :
# In[28]:
help(hash)
# In[29]:
hash(1) # les entiers suffisamment petits sont hachés sur eux même
hash(2**2399)
hash("1")
# In[30]:
hash("Réfléchissez à l'impact écologique de TOUS les aspects de votre vie !")
# - Les détails d'implémentations de `hash` vont au delà de la portée de ce cours.
# - Voir [cette démonstration](http://people.irisa.fr/Francois.Schwarzentruber/hash_tables_demo/) pour des exemples de fonctions de hachage.
# ### Pour l'exemple ici
# - Pour l'implémentation ici, on va utiliser la fonction `f(x) = hash(x) % m`, où `taille` sera un paramètre de la table.
# - L'avantage est que l'on pourra stocker n'importe quel objet Python (enfin, n'importe quel objet hachable, cf. [cette explication](https://stackoverflow.com/questions/14535730/what-does-hashable-mean-in-python)).
#
# In[31]:
def homemadeHash(m=1024):
def f(x):
return hash(x) % m
return f
# In[32]:
class SetWithHashTable(SetWithNonPrimOperations):
""" Hash table with linked chaining: each cell uses a Python list to store the values."""
sizeMax = 1024
def __init__(self, size=sizeMax):
""" Create a new empty hash table."""
self.size = size
self.hash = homemadeHash(size)
self.table = [ [] for _ in range(self.size) ]
def __len__(self):
""" Return n the current size of the set.
- Takes O(m) time in all cases.
"""
return sum(len(cell) for cell in self.table)
def contains(self, value):
""" Test if value is in the set.
- Takes O(k) for k the length of the cell containing the value.
"""
k = self.hash(value)
return value in self.table[k]
__contains__ = contains
def add(self, value):
""" Add value in the set if it is not present."""
k = self.hash(value)
if value not in self.table[k]:
self.table[k].append(value)
def pop(self, value):
""" Remove value in the set if it is present."""
k = self.hash(value)
if value in self.table[k]:
self.table[k].remove(value)
def values(self):
""" Return a fresh list of the values of the set.
- Takes O(n) time in worst case."""
values = []
for cell in self.table:
for value in cell:
values.append(value)
return values
# In[33]:
un_petit_test_avec_une_structure_densemble(SetWithHashTable)
# Et maintenant quelques tests :
# In[34]:
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithHashTable, size=10, max_value=10, min_value=0)')
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithHashTable, size=10, max_value=1000, min_value=0)')
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithHashTable, size=1000, max_value=10, min_value=0)')
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithHashTable, size=100, max_value=100, min_value=0)')
# In[35]:
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithHashTable, size=1000, max_value=1000, min_value=0)')
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithHashTable, size=1000, max_value=1000_000, min_value=0)')
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithHashTable, size=1000, max_value=1000_000_000, min_value=0)')
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithHashTable, size=1000, max_value=1000_000_000_000, min_value=0)')
# La complexité (amortie) des opérations semble aussi indépendant de la taille des valeurs hachées (c'est logique, vu le modulo dans la fonction $f(x)$), et linéaire dans la taille des ensembles.
# In[36]:
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithHashTable, size=1000_000, max_value=1000, min_value=0)')
#%timeit random_add_remove_test(SetWithHashTable, size=1000_000, max_value=1000_000, min_value=0)
#%timeit random_add_remove_test(SetWithHashTable, size=1000_000, max_value=1000_000_000, min_value=0)
#%timeit random_add_remove_test(SetWithHashTable, size=1000_000, max_value=1000_000_000_000, min_value=0)
# On montre plus bas que cette implémentation "maison" en pure Python est raisonnablement efficace !
# ----
# ## Implémentation avec des arbres binaires de recherche ?
#
# Pour plus de détails sur les arbres binaires de recherche, cf. le cours, le chapitre 12 du livre de référence "Algorithmique" de Cormen et al, et sur Internet.
#
#
#
# Les opérations de base sur l'ensemble représenté par la table seront réalisées comme suit :
#
# - Lorsqu'on ajoute une valeur $v$ à la table :
# + on calcule $j = f(v)$,
# + on ajoute $v$ à l'ensemble en position $j$ du tableau :
# * si c'est une liste chaînée par exemple, on créée une nouvelle liste contenant $v$ ou on ajoute $v$ à la fin de la liste chaînée,
# * si c'est une autre table de hachage, on l'ajoute en utilisant la primitive de la table,
# * etc
#
# - Lorsque l'on veut tester l'appartenance de $v$ à la table :
# + on calcule $j = f(v)$ (le numéro de la cellule contenant $v$, on parle parfois aussi d'alvéole),
# + on test si $v$ appartient à la liste / l'ensemble stocké en position $j$ du tableau.
#
# - La suppression fonctionne comme l'ajout.
# ### Comment stocker les plus petits ensembles ?
# - A première vue, on est face à une idée stupide : pour stocker un ensemble, on en stocke $m$…
# - Mais si la fonction de hachage est bien faite, si elle envoie les données $x \in D$ sur les $m$ différentes valeurs uniformément (en gros si $\forall j\in\{0,\dots,m\}, \# \{ x \in D : f(x) = j\} \simeq \frac{1}{m}$)
# - Les opérations de base sur les sous ensembles (les alvéoles) sont en complexités (au pire cas) linéaires dans la taille de ces sous ensembles, ce qui dépend du remplissage actuel de la table.
# Par exemple, avec $m = 20$, la fonction $f(x) = x \mod 20$ et des valeurs qui sont des entiers aléatoirement tirés (cf. [cette page de démonstration](http://people.irisa.fr/Francois.Schwarzentruber/hash_tables_demo/)) :
#
# 0 |_| --> []
# 1 |_| --> [98281,92581,11221]
# 2 |_| --> [91422,84022,65742,55322,59162]
# 3 |_| --> [64583,43563]
# 4 |_| --> []
# 5 |_| --> [1665,1585]
# 6 |_| --> [80986,80446,95966,28446,74726]
# 7 |_| --> [40867,86987,47907]
# 8 |_| --> [86268,31908,21688,59068,50448]
# 9 |_| --> [65989,38369,69769]
# 10 |_| --> [8670]
# 11 |_| --> [27211,99291]
# 12 |_| --> [43532]
# 13 |_| --> [55033,3873,76353]
# 14 |_| --> [74734]
# 15 |_| --> [36075,62495,42015,75435,26415]
# 16 |_| --> [85336,21856,18376,46436,64516]
# 17 |_| --> [66117,95857]
# 18 |_| --> [76438]
# 19 |_| --> []
#
# Par exemples :
# - Ici, chercher l'appartenance de 76438 à l'ensemble se fera en deux opérations : calculer $f(76438)=18$, puis en cherchant (en une seule opération) $76438$ dans `T[18]=` $[76438]$.
# - Chercher $59068$ va trouver la cellule $f(59068) = 8$, qui contient 5 valeurs, et donc trouver $59068$ dans la liste $[86268,31908,21688,59068,50448]$ prend quatre opérations.
# ### Choix de la fonction de hachage
# - Il existe plein de fonction de hachage pour différentes utilisations.
# - Pour des entiers, on peut prendre $f(x) = x \mod m$ et adapter $m$ en fonction des propriétés voulues par notre structure.
# + Plus $m$ est grand, plus les opérations seront rapides mais plus on consomme de mémoire, inversement un plus petit $m$ réduit l'impact mémoire mais augmente l'impact temps.
# + En fait, si nos entiers sont entre $0$ et $M$, on peut avoir les deux cas extrêmes suivants :
# * la pire solution vis à vis du temps de calcul est d'utiliser $m = 1$, tous les entiers sont stockés dans la même liste. On a donc une complexité en $O(n)$ pour les opérations de base, cf. plus haut.
# * la meilleure solution vis à vis du temps de calcul est d'utiliser $m = M$, ie. la table de hachage est juste un vecteur de bit, où la case $j$ vaut $T[j]=[j]$ ssi $j$ est dans la table. Chaque entier est stocké dans sa propre liste, de taille vide ou de taille 1. On a donc une complexité en $O(1)$ pour les opérations de base, cf. plus haut.
# * choisir un $m$ intermédiaire, par exemple $m = O(\log(M))$, peut permettre de balancer entre les deux extrêmes.
#
# - Pour des chaînes de caractères, on peut faire la somme des hachés de chaque caractères, modulo un certain nombre, ou n'importe quelle idée de ce genre.
#
# - Python utilise la fonction `hash()` :
# In[28]:
help(hash)
# In[29]:
hash(1) # les entiers suffisamment petits sont hachés sur eux même
hash(2**2399)
hash("1")
# In[30]:
hash("Réfléchissez à l'impact écologique de TOUS les aspects de votre vie !")
# - Les détails d'implémentations de `hash` vont au delà de la portée de ce cours.
# - Voir [cette démonstration](http://people.irisa.fr/Francois.Schwarzentruber/hash_tables_demo/) pour des exemples de fonctions de hachage.
# ### Pour l'exemple ici
# - Pour l'implémentation ici, on va utiliser la fonction `f(x) = hash(x) % m`, où `taille` sera un paramètre de la table.
# - L'avantage est que l'on pourra stocker n'importe quel objet Python (enfin, n'importe quel objet hachable, cf. [cette explication](https://stackoverflow.com/questions/14535730/what-does-hashable-mean-in-python)).
#
# In[31]:
def homemadeHash(m=1024):
def f(x):
return hash(x) % m
return f
# In[32]:
class SetWithHashTable(SetWithNonPrimOperations):
""" Hash table with linked chaining: each cell uses a Python list to store the values."""
sizeMax = 1024
def __init__(self, size=sizeMax):
""" Create a new empty hash table."""
self.size = size
self.hash = homemadeHash(size)
self.table = [ [] for _ in range(self.size) ]
def __len__(self):
""" Return n the current size of the set.
- Takes O(m) time in all cases.
"""
return sum(len(cell) for cell in self.table)
def contains(self, value):
""" Test if value is in the set.
- Takes O(k) for k the length of the cell containing the value.
"""
k = self.hash(value)
return value in self.table[k]
__contains__ = contains
def add(self, value):
""" Add value in the set if it is not present."""
k = self.hash(value)
if value not in self.table[k]:
self.table[k].append(value)
def pop(self, value):
""" Remove value in the set if it is present."""
k = self.hash(value)
if value in self.table[k]:
self.table[k].remove(value)
def values(self):
""" Return a fresh list of the values of the set.
- Takes O(n) time in worst case."""
values = []
for cell in self.table:
for value in cell:
values.append(value)
return values
# In[33]:
un_petit_test_avec_une_structure_densemble(SetWithHashTable)
# Et maintenant quelques tests :
# In[34]:
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithHashTable, size=10, max_value=10, min_value=0)')
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithHashTable, size=10, max_value=1000, min_value=0)')
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithHashTable, size=1000, max_value=10, min_value=0)')
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithHashTable, size=100, max_value=100, min_value=0)')
# In[35]:
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithHashTable, size=1000, max_value=1000, min_value=0)')
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithHashTable, size=1000, max_value=1000_000, min_value=0)')
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithHashTable, size=1000, max_value=1000_000_000, min_value=0)')
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithHashTable, size=1000, max_value=1000_000_000_000, min_value=0)')
# La complexité (amortie) des opérations semble aussi indépendant de la taille des valeurs hachées (c'est logique, vu le modulo dans la fonction $f(x)$), et linéaire dans la taille des ensembles.
# In[36]:
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithHashTable, size=1000_000, max_value=1000, min_value=0)')
#%timeit random_add_remove_test(SetWithHashTable, size=1000_000, max_value=1000_000, min_value=0)
#%timeit random_add_remove_test(SetWithHashTable, size=1000_000, max_value=1000_000_000, min_value=0)
#%timeit random_add_remove_test(SetWithHashTable, size=1000_000, max_value=1000_000_000_000, min_value=0)
# On montre plus bas que cette implémentation "maison" en pure Python est raisonnablement efficace !
# ----
# ## Implémentation avec des arbres binaires de recherche ?
#
# Pour plus de détails sur les arbres binaires de recherche, cf. le cours, le chapitre 12 du livre de référence "Algorithmique" de Cormen et al, et sur Internet.
#
#  # ### Un nœud d'un arbre binaire
#
# - Un nœud contient une clé, `key`, et éventuellement une valeur associée,
# - Ainsi que des pointeurs vers d'autres nœuds (éventuellement) : parent, fils gauche (`left`) et fils droit (`right`).
# In[37]:
class NodeTree():
def __init__(self, key, value=None, left=None, right=None, parent=None):
self.key = key
self.value = value
self.left = left
self.right = right
self.parent = parent
def __str__(self):
if self.value is None: # key is also the stored value
return "{}".format(self.key)
else:
return "{}: {}".format(self.key, self.value)
# --- First algorithm on this BST: compute the height ---
def height(self):
""" Compute the height h of the Binary Search Tree.
- Takes a time in O(n). Could be stored and take a time O(1) but it's useless."""
h = 0
if self.left is not None:
h = max(h, 1 + self.left.height())
if self.right is not None:
h = max(h, 1 + self.right.height())
return h
# --- Keys and values ---
def keys(self):
""" Extract the keys from the Binary Search Tree.
- It is a generator, use list(self.keys()) to have a list.
- Takes a time in O(n) for n keys."""
if self is not None:
if self.left is not None:
yield from self.left.keys()
yield self.key
if self.right is not None:
yield from self.right.keys()
def values(self):
""" Extract the values from the Binary Search Tree.
- UIt is a generator, use list(self.keys()) to have a list.
- Takes a time in O(n) for n values."""
if self is not None:
if self.left is not None:
yield from self.left.values()
yield self.value
if self.right is not None:
yield from self.right.values()
# --- Search ---
def search(self, key):
""" Search for the NodeTree(...) associated to the queried key. Returns None if not found.
- Takes a time in O(h) = O(n) in worst case for n keys/values (if wrongly balanced)."""
if key is None or self.key is None:
raise KeyError
if self.key == key:
return self
elif key < self.key and self.left is not None:
return self.left.search(key)
elif key > self.key and self.right is not None:
return self.right.search(key)
raise KeyError
# --- Looking for minimum / successor ---
def minimum(self):
""" Search for the NodeTree(...) associated to the minimum key.
- Takes a time in O(h) = O(n) in worst case for n keys/values (if wrongly balanced)."""
if self.left is None:
return self
else:
return self.left.minimum()
def successor(self, node):
""" Search for the NodeTree(...) successor of the queried node (ie. the node with smallest key >= node.key).
- Takes a time in O(h) = O(n) in worst case for n keys/values (if wrongly balanced)."""
if node.right is not None:
return node.right.minimum()
x = node
y = x.parent
while y is not None and x == y.right():
x = y
y = x.parent
return y
# --- Looking for maximum / predecessor ---
def maximum(self):
""" Search for the NodeTree(...) associated to the maximum key.
- Takes a time in O(h) = O(n) in worst case for n keys/values (if wrongly balanced)."""
if self is None:
return self
else:
return self.right.maximum()
def predecessor(self, node):
""" Search for the NodeTree(...) predecessor of the queried node (ie. the node with largest key <= node.key).
- Takes a time in O(h) = O(n) in worst case for n keys/values (if wrongly balanced)."""
if node.left is not None:
return node.left.maximum()
x = node
y = x.parent
while y is not None and x == y.left():
x = y
y = x.parent
return y
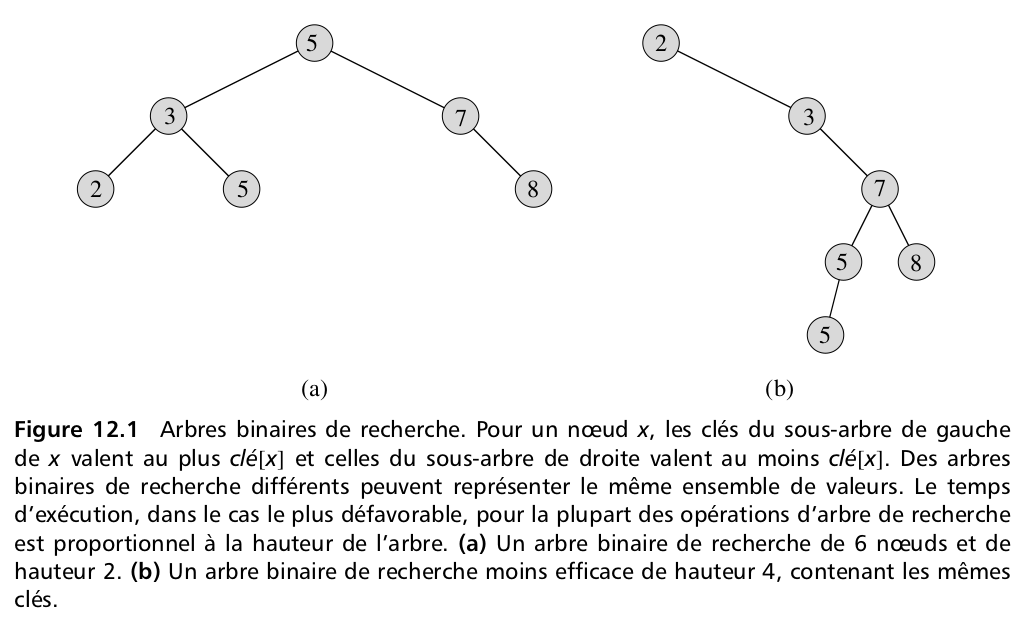
# Les deux exemples de la figure se représentent comme ça :
# - Pour l'arbre équilibré de la figure (a) ci dessus :
# In[38]:
n_5 = NodeTree(5)
n_3 = NodeTree(3)
n_2 = NodeTree(2)
n_5bis = NodeTree(5)
n_7 = NodeTree(7)
n_8 = NodeTree(8)
n_5.left, n_5.right = n_3, n_7
n_3.left, n_3.right = n_2, n_5bis
n_7.right = n_8
n_3.parent, n_7.parent = n_5, n_5
n_2.parent, n_5bis.parent = n_3, n_3
n_8.parent = n_7
# - Pour l'arbre non équilibré de la figure (b) ci dessus :
# In[39]:
n_5 = NodeTree(5)
n_3 = NodeTree(3)
n_2 = NodeTree(2)
n_5bis = NodeTree(5)
n_7 = NodeTree(7)
n_8 = NodeTree(8)
n_2.right = n_3 ; n_3.parent = n_2
n_3.right = n_7 ; n_7.parent = n_3
n_7.left = n_5 ; n_5.parent = n_7
n_5.left = n_5bis ; n_5bis.parent = n_5
n_7.right = n_8 ; n_8.parent = n_7
# ### Un arbre binaire de recherche
# Et maintenant pour la classe :
# In[40]:
class BinarySearchTree():
def __init__(self):
self.root = None
self.size = 0
# --- Looking for a (key,value) ---
def get(self, key):
""" Search for the value associated to the queried key.
- Takes a time in O(h) = O(n) in worst case for n keys/values (if wrongly balanced)."""
if self.root is None:
raise KeyError
node = self.root.search(key)
if node is not None:
return node.value
raise KeyError
def contains(self, value):
""" Test if value is in the set.
- Takes O(h) for h the height of the BST.
"""
try:
_ = self.get(value)
return True
except KeyError:
return False
__contains__ = contains
# --- Looking for minimum / successor ---
def minimum(self):
""" Search for the NodeTree(...) associated to the minimum key.
- Takes a time in O(h) = O(n) in worst case for n keys/values (if wrongly balanced)."""
if self.root is not None:
return self.root.minimum()
raise KeyError
def successor(self, node):
""" Search for the NodeTree(...) successor of the queried node (ie. the node with smallest key >= node.key).
- Takes a time in O(h) = O(n) in worst case for n keys/values (if wrongly balanced)."""
if self.root is not None:
return self.root.successor(node)
raise KeyError
# --- Looking for maximum / predecessor ---
def maximum(self):
""" Search for the NodeTree(...) associated to the maximum key.
- Takes a time in O(h) = O(n) in worst case for n keys/values (if wrongly balanced)."""
if self.root is not None:
return self.root.maximum()
raise KeyError
def predecessor(self, node):
""" Search for the NodeTree(...) predecessor of the queried node (ie. the node with largest key <= node.key).
- Takes a time in O(h) = O(n) in worst case for n keys/values (if wrongly balanced)."""
if self.root is not None:
return self.root.predecessor(node)
raise KeyError
# --- Insertion ---
def insert(self, key, value=None):
""" Insert a new key (or (key, value)) in the BST.
- Takes a time in O(h) = O(n) in worst case for n keys/values (if wrongly balanced)."""
if key in self:
value_mapped = self.get(key)
if value == value_mapped:
return # nothing to do, the pair (key, value) is already in the set!
self.size += 1
z = NodeTree(key, value=value)
y = None
x = self.root
while x is not None:
y = x
if z.key < x.key:
x = x.left
else:
x = x.right
z.parent = y
if y is None: # the tree was empty!
self.root = z
elif z.key < y.key:
y.left = z
else:
y.right = z
# --- Supression/deletion: it is harder! ---
def delete(self, key):
""" Delete the key in the BST.
- Takes a time in O(h) = O(n) in worst case for n keys/values (if wrongly balanced)."""
if self.root is None:
raise KeyError
node_to_delete = self.root.search(key)
if node_to_delete is None:
raise KeyError
self.size -= 1
z = node_to_delete
# ligne 1-3 Cormen [Arbre-Supprimer]
if z.left is None or z.right is None:
y = z
else:
y = self.successor(z)
# ligne 4-6 Cormen [Arbre-Supprimer]
if y.left is not None:
x = y.left
else:
x = y.right
# ligne 7-8 Cormen [Arbre-Supprimer]
if x is not None:
x.parent = y.parent
# ligne 9-13 Cormen [Arbre-Supprimer]
if y.parent is None:
self.root = x
elif y == y.parent.left:
y.parent.left = x
else:
y.parent.right = x
# ligne 14-16 Cormen [Arbre-Supprimer]
if y != z:
z.key, z.value = y.key, y.value
return y
# --- Keys and values ---
def keys(self):
""" Extract the keys from the Binary Search Tree.
- Takes a time in O(n) for n keys."""
if self.root is not None:
return list(self.root.keys())
return []
def values(self):
""" Extract the values from the Binary Search Tree.
- Takes a time in O(n) for n values."""
if self.root is not None:
return list(self.root.values())
return []
# --- Length, height ---
def __len__(self):
return self.size
def height(self):
if self.root is not None:
return self.root.height()
else:
return -1
# --- Draw the graph ---
def to_nxgraph(self):
G = nx.DiGraph()
def go_down(node):
if node.left is not None:
G.add_node(node.left)
G.add_edge(node, node.left)
go_down(node.left)
if node.right is not None:
G.add_node(node.right)
G.add_edge(node, node.right)
go_down(node.right)
if self.root is not None:
G.add_node(self.root)
go_down(self.root)
return G
def plot(self):
G = self.to_nxgraph()
pos = nx.drawing.nx_agraph.graphviz_layout(G, prog='dot')
return nx.draw(G, pos, with_labels=True)
# Dessiner l'ABR est facile, avec la bibliothèque [NetworkX](https://networkx.github.io/).
# In[41]:
import matplotlib.pyplot as plt
import networkx as nx
# Quelques exemples et quelques tests :
# In[42]:
keys = list(range(10))
values = [ "V{}".format(key) for key in keys ]
# In[43]:
BST = BinarySearchTree()
for (k, v) in zip(keys, values):
print("Clés de l'ABR =", list(BST.keys()), "Valeurs de l'ABR =", list(BST.values()), "Hauteur de l'ABR =", BST.height(), "Taille de l'ABR =", BST.size)
BST.insert(k, v)
print("Clés de l'ABR =", list(BST.keys()), "Valeurs de l'ABR =", list(BST.values()), "Hauteur de l'ABR =", BST.height(), "Taille de l'ABR =", BST.size)
# In[44]:
BST.plot()
# Maintenant si l'ordre d'insertion des clés n'est plus monotone, on va éviter d'avoir un arbre binaire réduit à une chaîne.
# In[45]:
BST = BinarySearchTree()
keys_values = list(zip(keys, values))
import random
random.seed(1234)
random.shuffle(keys_values)
print("Clés et valeurs =", keys_values)
for (k, v) in keys_values:
BST.insert(k, v)
print("Clés de l'ABR =", list(BST.keys()), "Valeurs de l'ABR =", list(BST.values()), "Hauteur de l'ABR =", BST.height(), "Taille de l'ABR =", BST.size)
for k in keys:
print("Valeur associée à", k, "=", BST.get(k))
# In[46]:
BST.plot()
# On voit ici que si on insert les clés dans un ordre "aléatoire" (ie. un ordre qui a peu de chance de donner un cas trop dégénéré), l'arbre binaire ne sera *pas* réduit à une chaîne et il aura une hauteur bien plus faible que sa taille.
# ### Ensemble avec un Arbre Binaire de Recherche
#
# C'est très simple, on va stocker les valeurs de l'ensemble dans les clés de l'ABR et on utilise des valeurs vides.
#
# L'objectif est d'avoir une complexité en $\mathcal{O}(\log(n))$ pour l'ajout, l'appartenance et le retrait de valeurs, si les valeurs ajoutées sont insérées dans un ordre aléatoire.
# Comme pour la table de hachage, la complexité au pire des cas restera linéaire en $\Omega(n)$ (si on construit un ABR réduit à une chaîne linéaire, comme l'exemple plus haut).
# In[47]:
class SetWithBinarySearchTree(BinarySearchTree, SetWithNonPrimOperations):
""" A set storing its values in a Binary Search Tree."""
def values(self): # hack: we only use keys as values
return self.keys()
def add(self, value):
""" Add value in the set if it is not present."""
key, value = value, None
return self.insert(key, value=value)
def pop(self, value):
""" Remove value in the set if it is present."""
return self.delete(value)
# Et pour la dernière structure implémentée ici, on teste :
# In[48]:
un_petit_test_avec_une_structure_densemble(SetWithBinarySearchTree)
# Et maintenant quelques tests :
# In[49]:
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithBinarySearchTree, size=10, max_value=10, min_value=0)')
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithBinarySearchTree, size=10, max_value=1000, min_value=0)')
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithBinarySearchTree, size=1000, max_value=10, min_value=0)')
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithBinarySearchTree, size=100, max_value=100, min_value=0)')
# In[50]:
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithBinarySearchTree, size=100, max_value=1000_000, min_value=-1000_000)')
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithBinarySearchTree, size=1000, max_value=1000_000, min_value=-1000_000)')
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithBinarySearchTree, size=10000, max_value=1000_000, min_value=-1000_000)')
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithBinarySearchTree, size=100000, max_value=1000_000, min_value=-1000_000)')
# ## Comparaison des différentes implémentations
# In[51]:
print("\n- Pour la classe", NativeSet)
get_ipython().run_line_magic('timeit', 'random_add_remove_test(NativeSet, size=1000, max_value=1000_000, min_value=0)')
print("\n- Pour la classe", SetWithList)
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithList, size=1000, max_value=1000_000, min_value=0)')
print("\n- Pour la classe", SetWithInt)
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithInt, size=1000, max_value=1000_000, min_value=0)')
print("\n- Pour la classe", SetWithHashTable)
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithHashTable, size=1000, max_value=1000_000, min_value=0)')
print("\n- Pour la classe", SetWithBinarySearchTree)
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithBinarySearchTree, size=1000, max_value=1000_000, min_value=0)')
# In[52]:
print("\n- Pour la classe", NativeSet)
get_ipython().run_line_magic('timeit', 'random_add_remove_test(NativeSet, size=10_000, max_value=1000_000, min_value=0)')
print("\n- Pour la classe", SetWithList)
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithList, size=10_000, max_value=1000_000, min_value=0)')
print("\n- Pour la classe", SetWithHashTable)
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithHashTable, size=10_000, max_value=1000_000, min_value=0)')
print("\n- Pour la classe", SetWithBinarySearchTree)
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithBinarySearchTree, size=10_000, max_value=1000_000, min_value=0)')
# In[53]:
print("\n- Pour la classe", NativeSet)
get_ipython().run_line_magic('timeit', 'random_add_remove_test(NativeSet, size=20_000, max_value=1000_000, min_value=0)')
print("\n- Pour la classe", SetWithList)
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithList, size=20_000, max_value=1000_000, min_value=0)')
print("\n- Pour la classe", SetWithHashTable)
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithHashTable, size=20_000, max_value=1000_000, min_value=0)')
print("\n- Pour la classe", SetWithBinarySearchTree)
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithBinarySearchTree, size=20_000, max_value=1000_000, min_value=0)')
# In[56]:
print("\n- Pour la classe", NativeSet)
get_ipython().run_line_magic('timeit', 'random_add_remove_test(NativeSet, size=30_000, max_value=1000_000, min_value=0)')
print("\n- Pour la classe", SetWithList)
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithList, size=30_000, max_value=1000_000, min_value=0)')
print("\n- Pour la classe", SetWithHashTable)
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithHashTable, size=30_000, max_value=1000_000, min_value=0)')
print("\n- Pour la classe", SetWithBinarySearchTree)
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithBinarySearchTree, size=30_000, max_value=1000_000, min_value=0)')
# On voit que notre implémentation "maison" avec des tables de hachage est quasiment aussi efficace que l'implémentation native (en C !) de Python avec la classe `set` (qui utilise aussi une table de hachage, mais écrite en C !).
# ## Conclusion
#
# C'est bon pour aujourd'hui !
# ### Un nœud d'un arbre binaire
#
# - Un nœud contient une clé, `key`, et éventuellement une valeur associée,
# - Ainsi que des pointeurs vers d'autres nœuds (éventuellement) : parent, fils gauche (`left`) et fils droit (`right`).
# In[37]:
class NodeTree():
def __init__(self, key, value=None, left=None, right=None, parent=None):
self.key = key
self.value = value
self.left = left
self.right = right
self.parent = parent
def __str__(self):
if self.value is None: # key is also the stored value
return "{}".format(self.key)
else:
return "{}: {}".format(self.key, self.value)
# --- First algorithm on this BST: compute the height ---
def height(self):
""" Compute the height h of the Binary Search Tree.
- Takes a time in O(n). Could be stored and take a time O(1) but it's useless."""
h = 0
if self.left is not None:
h = max(h, 1 + self.left.height())
if self.right is not None:
h = max(h, 1 + self.right.height())
return h
# --- Keys and values ---
def keys(self):
""" Extract the keys from the Binary Search Tree.
- It is a generator, use list(self.keys()) to have a list.
- Takes a time in O(n) for n keys."""
if self is not None:
if self.left is not None:
yield from self.left.keys()
yield self.key
if self.right is not None:
yield from self.right.keys()
def values(self):
""" Extract the values from the Binary Search Tree.
- UIt is a generator, use list(self.keys()) to have a list.
- Takes a time in O(n) for n values."""
if self is not None:
if self.left is not None:
yield from self.left.values()
yield self.value
if self.right is not None:
yield from self.right.values()
# --- Search ---
def search(self, key):
""" Search for the NodeTree(...) associated to the queried key. Returns None if not found.
- Takes a time in O(h) = O(n) in worst case for n keys/values (if wrongly balanced)."""
if key is None or self.key is None:
raise KeyError
if self.key == key:
return self
elif key < self.key and self.left is not None:
return self.left.search(key)
elif key > self.key and self.right is not None:
return self.right.search(key)
raise KeyError
# --- Looking for minimum / successor ---
def minimum(self):
""" Search for the NodeTree(...) associated to the minimum key.
- Takes a time in O(h) = O(n) in worst case for n keys/values (if wrongly balanced)."""
if self.left is None:
return self
else:
return self.left.minimum()
def successor(self, node):
""" Search for the NodeTree(...) successor of the queried node (ie. the node with smallest key >= node.key).
- Takes a time in O(h) = O(n) in worst case for n keys/values (if wrongly balanced)."""
if node.right is not None:
return node.right.minimum()
x = node
y = x.parent
while y is not None and x == y.right():
x = y
y = x.parent
return y
# --- Looking for maximum / predecessor ---
def maximum(self):
""" Search for the NodeTree(...) associated to the maximum key.
- Takes a time in O(h) = O(n) in worst case for n keys/values (if wrongly balanced)."""
if self is None:
return self
else:
return self.right.maximum()
def predecessor(self, node):
""" Search for the NodeTree(...) predecessor of the queried node (ie. the node with largest key <= node.key).
- Takes a time in O(h) = O(n) in worst case for n keys/values (if wrongly balanced)."""
if node.left is not None:
return node.left.maximum()
x = node
y = x.parent
while y is not None and x == y.left():
x = y
y = x.parent
return y
# Les deux exemples de la figure se représentent comme ça :
# - Pour l'arbre équilibré de la figure (a) ci dessus :
# In[38]:
n_5 = NodeTree(5)
n_3 = NodeTree(3)
n_2 = NodeTree(2)
n_5bis = NodeTree(5)
n_7 = NodeTree(7)
n_8 = NodeTree(8)
n_5.left, n_5.right = n_3, n_7
n_3.left, n_3.right = n_2, n_5bis
n_7.right = n_8
n_3.parent, n_7.parent = n_5, n_5
n_2.parent, n_5bis.parent = n_3, n_3
n_8.parent = n_7
# - Pour l'arbre non équilibré de la figure (b) ci dessus :
# In[39]:
n_5 = NodeTree(5)
n_3 = NodeTree(3)
n_2 = NodeTree(2)
n_5bis = NodeTree(5)
n_7 = NodeTree(7)
n_8 = NodeTree(8)
n_2.right = n_3 ; n_3.parent = n_2
n_3.right = n_7 ; n_7.parent = n_3
n_7.left = n_5 ; n_5.parent = n_7
n_5.left = n_5bis ; n_5bis.parent = n_5
n_7.right = n_8 ; n_8.parent = n_7
# ### Un arbre binaire de recherche
# Et maintenant pour la classe :
# In[40]:
class BinarySearchTree():
def __init__(self):
self.root = None
self.size = 0
# --- Looking for a (key,value) ---
def get(self, key):
""" Search for the value associated to the queried key.
- Takes a time in O(h) = O(n) in worst case for n keys/values (if wrongly balanced)."""
if self.root is None:
raise KeyError
node = self.root.search(key)
if node is not None:
return node.value
raise KeyError
def contains(self, value):
""" Test if value is in the set.
- Takes O(h) for h the height of the BST.
"""
try:
_ = self.get(value)
return True
except KeyError:
return False
__contains__ = contains
# --- Looking for minimum / successor ---
def minimum(self):
""" Search for the NodeTree(...) associated to the minimum key.
- Takes a time in O(h) = O(n) in worst case for n keys/values (if wrongly balanced)."""
if self.root is not None:
return self.root.minimum()
raise KeyError
def successor(self, node):
""" Search for the NodeTree(...) successor of the queried node (ie. the node with smallest key >= node.key).
- Takes a time in O(h) = O(n) in worst case for n keys/values (if wrongly balanced)."""
if self.root is not None:
return self.root.successor(node)
raise KeyError
# --- Looking for maximum / predecessor ---
def maximum(self):
""" Search for the NodeTree(...) associated to the maximum key.
- Takes a time in O(h) = O(n) in worst case for n keys/values (if wrongly balanced)."""
if self.root is not None:
return self.root.maximum()
raise KeyError
def predecessor(self, node):
""" Search for the NodeTree(...) predecessor of the queried node (ie. the node with largest key <= node.key).
- Takes a time in O(h) = O(n) in worst case for n keys/values (if wrongly balanced)."""
if self.root is not None:
return self.root.predecessor(node)
raise KeyError
# --- Insertion ---
def insert(self, key, value=None):
""" Insert a new key (or (key, value)) in the BST.
- Takes a time in O(h) = O(n) in worst case for n keys/values (if wrongly balanced)."""
if key in self:
value_mapped = self.get(key)
if value == value_mapped:
return # nothing to do, the pair (key, value) is already in the set!
self.size += 1
z = NodeTree(key, value=value)
y = None
x = self.root
while x is not None:
y = x
if z.key < x.key:
x = x.left
else:
x = x.right
z.parent = y
if y is None: # the tree was empty!
self.root = z
elif z.key < y.key:
y.left = z
else:
y.right = z
# --- Supression/deletion: it is harder! ---
def delete(self, key):
""" Delete the key in the BST.
- Takes a time in O(h) = O(n) in worst case for n keys/values (if wrongly balanced)."""
if self.root is None:
raise KeyError
node_to_delete = self.root.search(key)
if node_to_delete is None:
raise KeyError
self.size -= 1
z = node_to_delete
# ligne 1-3 Cormen [Arbre-Supprimer]
if z.left is None or z.right is None:
y = z
else:
y = self.successor(z)
# ligne 4-6 Cormen [Arbre-Supprimer]
if y.left is not None:
x = y.left
else:
x = y.right
# ligne 7-8 Cormen [Arbre-Supprimer]
if x is not None:
x.parent = y.parent
# ligne 9-13 Cormen [Arbre-Supprimer]
if y.parent is None:
self.root = x
elif y == y.parent.left:
y.parent.left = x
else:
y.parent.right = x
# ligne 14-16 Cormen [Arbre-Supprimer]
if y != z:
z.key, z.value = y.key, y.value
return y
# --- Keys and values ---
def keys(self):
""" Extract the keys from the Binary Search Tree.
- Takes a time in O(n) for n keys."""
if self.root is not None:
return list(self.root.keys())
return []
def values(self):
""" Extract the values from the Binary Search Tree.
- Takes a time in O(n) for n values."""
if self.root is not None:
return list(self.root.values())
return []
# --- Length, height ---
def __len__(self):
return self.size
def height(self):
if self.root is not None:
return self.root.height()
else:
return -1
# --- Draw the graph ---
def to_nxgraph(self):
G = nx.DiGraph()
def go_down(node):
if node.left is not None:
G.add_node(node.left)
G.add_edge(node, node.left)
go_down(node.left)
if node.right is not None:
G.add_node(node.right)
G.add_edge(node, node.right)
go_down(node.right)
if self.root is not None:
G.add_node(self.root)
go_down(self.root)
return G
def plot(self):
G = self.to_nxgraph()
pos = nx.drawing.nx_agraph.graphviz_layout(G, prog='dot')
return nx.draw(G, pos, with_labels=True)
# Dessiner l'ABR est facile, avec la bibliothèque [NetworkX](https://networkx.github.io/).
# In[41]:
import matplotlib.pyplot as plt
import networkx as nx
# Quelques exemples et quelques tests :
# In[42]:
keys = list(range(10))
values = [ "V{}".format(key) for key in keys ]
# In[43]:
BST = BinarySearchTree()
for (k, v) in zip(keys, values):
print("Clés de l'ABR =", list(BST.keys()), "Valeurs de l'ABR =", list(BST.values()), "Hauteur de l'ABR =", BST.height(), "Taille de l'ABR =", BST.size)
BST.insert(k, v)
print("Clés de l'ABR =", list(BST.keys()), "Valeurs de l'ABR =", list(BST.values()), "Hauteur de l'ABR =", BST.height(), "Taille de l'ABR =", BST.size)
# In[44]:
BST.plot()
# Maintenant si l'ordre d'insertion des clés n'est plus monotone, on va éviter d'avoir un arbre binaire réduit à une chaîne.
# In[45]:
BST = BinarySearchTree()
keys_values = list(zip(keys, values))
import random
random.seed(1234)
random.shuffle(keys_values)
print("Clés et valeurs =", keys_values)
for (k, v) in keys_values:
BST.insert(k, v)
print("Clés de l'ABR =", list(BST.keys()), "Valeurs de l'ABR =", list(BST.values()), "Hauteur de l'ABR =", BST.height(), "Taille de l'ABR =", BST.size)
for k in keys:
print("Valeur associée à", k, "=", BST.get(k))
# In[46]:
BST.plot()
# On voit ici que si on insert les clés dans un ordre "aléatoire" (ie. un ordre qui a peu de chance de donner un cas trop dégénéré), l'arbre binaire ne sera *pas* réduit à une chaîne et il aura une hauteur bien plus faible que sa taille.
# ### Ensemble avec un Arbre Binaire de Recherche
#
# C'est très simple, on va stocker les valeurs de l'ensemble dans les clés de l'ABR et on utilise des valeurs vides.
#
# L'objectif est d'avoir une complexité en $\mathcal{O}(\log(n))$ pour l'ajout, l'appartenance et le retrait de valeurs, si les valeurs ajoutées sont insérées dans un ordre aléatoire.
# Comme pour la table de hachage, la complexité au pire des cas restera linéaire en $\Omega(n)$ (si on construit un ABR réduit à une chaîne linéaire, comme l'exemple plus haut).
# In[47]:
class SetWithBinarySearchTree(BinarySearchTree, SetWithNonPrimOperations):
""" A set storing its values in a Binary Search Tree."""
def values(self): # hack: we only use keys as values
return self.keys()
def add(self, value):
""" Add value in the set if it is not present."""
key, value = value, None
return self.insert(key, value=value)
def pop(self, value):
""" Remove value in the set if it is present."""
return self.delete(value)
# Et pour la dernière structure implémentée ici, on teste :
# In[48]:
un_petit_test_avec_une_structure_densemble(SetWithBinarySearchTree)
# Et maintenant quelques tests :
# In[49]:
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithBinarySearchTree, size=10, max_value=10, min_value=0)')
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithBinarySearchTree, size=10, max_value=1000, min_value=0)')
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithBinarySearchTree, size=1000, max_value=10, min_value=0)')
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithBinarySearchTree, size=100, max_value=100, min_value=0)')
# In[50]:
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithBinarySearchTree, size=100, max_value=1000_000, min_value=-1000_000)')
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithBinarySearchTree, size=1000, max_value=1000_000, min_value=-1000_000)')
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithBinarySearchTree, size=10000, max_value=1000_000, min_value=-1000_000)')
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithBinarySearchTree, size=100000, max_value=1000_000, min_value=-1000_000)')
# ## Comparaison des différentes implémentations
# In[51]:
print("\n- Pour la classe", NativeSet)
get_ipython().run_line_magic('timeit', 'random_add_remove_test(NativeSet, size=1000, max_value=1000_000, min_value=0)')
print("\n- Pour la classe", SetWithList)
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithList, size=1000, max_value=1000_000, min_value=0)')
print("\n- Pour la classe", SetWithInt)
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithInt, size=1000, max_value=1000_000, min_value=0)')
print("\n- Pour la classe", SetWithHashTable)
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithHashTable, size=1000, max_value=1000_000, min_value=0)')
print("\n- Pour la classe", SetWithBinarySearchTree)
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithBinarySearchTree, size=1000, max_value=1000_000, min_value=0)')
# In[52]:
print("\n- Pour la classe", NativeSet)
get_ipython().run_line_magic('timeit', 'random_add_remove_test(NativeSet, size=10_000, max_value=1000_000, min_value=0)')
print("\n- Pour la classe", SetWithList)
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithList, size=10_000, max_value=1000_000, min_value=0)')
print("\n- Pour la classe", SetWithHashTable)
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithHashTable, size=10_000, max_value=1000_000, min_value=0)')
print("\n- Pour la classe", SetWithBinarySearchTree)
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithBinarySearchTree, size=10_000, max_value=1000_000, min_value=0)')
# In[53]:
print("\n- Pour la classe", NativeSet)
get_ipython().run_line_magic('timeit', 'random_add_remove_test(NativeSet, size=20_000, max_value=1000_000, min_value=0)')
print("\n- Pour la classe", SetWithList)
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithList, size=20_000, max_value=1000_000, min_value=0)')
print("\n- Pour la classe", SetWithHashTable)
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithHashTable, size=20_000, max_value=1000_000, min_value=0)')
print("\n- Pour la classe", SetWithBinarySearchTree)
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithBinarySearchTree, size=20_000, max_value=1000_000, min_value=0)')
# In[56]:
print("\n- Pour la classe", NativeSet)
get_ipython().run_line_magic('timeit', 'random_add_remove_test(NativeSet, size=30_000, max_value=1000_000, min_value=0)')
print("\n- Pour la classe", SetWithList)
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithList, size=30_000, max_value=1000_000, min_value=0)')
print("\n- Pour la classe", SetWithHashTable)
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithHashTable, size=30_000, max_value=1000_000, min_value=0)')
print("\n- Pour la classe", SetWithBinarySearchTree)
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithBinarySearchTree, size=30_000, max_value=1000_000, min_value=0)')
# On voit que notre implémentation "maison" avec des tables de hachage est quasiment aussi efficace que l'implémentation native (en C !) de Python avec la classe `set` (qui utilise aussi une table de hachage, mais écrite en C !).
# ## Conclusion
#
# C'est bon pour aujourd'hui !
 #
# Les opérations de base sur l'ensemble représenté par la table seront réalisées comme suit :
#
# - Lorsqu'on ajoute une valeur $v$ à la table :
# + on calcule $j = f(v)$,
# + on ajoute $v$ à l'ensemble en position $j$ du tableau :
# * si c'est une liste chaînée par exemple, on créée une nouvelle liste contenant $v$ ou on ajoute $v$ à la fin de la liste chaînée,
# * si c'est une autre table de hachage, on l'ajoute en utilisant la primitive de la table,
# * etc
#
# - Lorsque l'on veut tester l'appartenance de $v$ à la table :
# + on calcule $j = f(v)$ (le numéro de la cellule contenant $v$, on parle parfois aussi d'alvéole),
# + on test si $v$ appartient à la liste / l'ensemble stocké en position $j$ du tableau.
#
# - La suppression fonctionne comme l'ajout.
# ### Comment stocker les plus petits ensembles ?
# - A première vue, on est face à une idée stupide : pour stocker un ensemble, on en stocke $m$…
# - Mais si la fonction de hachage est bien faite, si elle envoie les données $x \in D$ sur les $m$ différentes valeurs uniformément (en gros si $\forall j\in\{0,\dots,m\}, \# \{ x \in D : f(x) = j\} \simeq \frac{1}{m}$)
# - Les opérations de base sur les sous ensembles (les alvéoles) sont en complexités (au pire cas) linéaires dans la taille de ces sous ensembles, ce qui dépend du remplissage actuel de la table.
# Par exemple, avec $m = 20$, la fonction $f(x) = x \mod 20$ et des valeurs qui sont des entiers aléatoirement tirés (cf. [cette page de démonstration](http://people.irisa.fr/Francois.Schwarzentruber/hash_tables_demo/)) :
#
# 0 |_| --> []
# 1 |_| --> [98281,92581,11221]
# 2 |_| --> [91422,84022,65742,55322,59162]
# 3 |_| --> [64583,43563]
# 4 |_| --> []
# 5 |_| --> [1665,1585]
# 6 |_| --> [80986,80446,95966,28446,74726]
# 7 |_| --> [40867,86987,47907]
# 8 |_| --> [86268,31908,21688,59068,50448]
# 9 |_| --> [65989,38369,69769]
# 10 |_| --> [8670]
# 11 |_| --> [27211,99291]
# 12 |_| --> [43532]
# 13 |_| --> [55033,3873,76353]
# 14 |_| --> [74734]
# 15 |_| --> [36075,62495,42015,75435,26415]
# 16 |_| --> [85336,21856,18376,46436,64516]
# 17 |_| --> [66117,95857]
# 18 |_| --> [76438]
# 19 |_| --> []
#
# Par exemples :
# - Ici, chercher l'appartenance de 76438 à l'ensemble se fera en deux opérations : calculer $f(76438)=18$, puis en cherchant (en une seule opération) $76438$ dans `T[18]=` $[76438]$.
# - Chercher $59068$ va trouver la cellule $f(59068) = 8$, qui contient 5 valeurs, et donc trouver $59068$ dans la liste $[86268,31908,21688,59068,50448]$ prend quatre opérations.
# ### Choix de la fonction de hachage
# - Il existe plein de fonction de hachage pour différentes utilisations.
# - Pour des entiers, on peut prendre $f(x) = x \mod m$ et adapter $m$ en fonction des propriétés voulues par notre structure.
# + Plus $m$ est grand, plus les opérations seront rapides mais plus on consomme de mémoire, inversement un plus petit $m$ réduit l'impact mémoire mais augmente l'impact temps.
# + En fait, si nos entiers sont entre $0$ et $M$, on peut avoir les deux cas extrêmes suivants :
# * la pire solution vis à vis du temps de calcul est d'utiliser $m = 1$, tous les entiers sont stockés dans la même liste. On a donc une complexité en $O(n)$ pour les opérations de base, cf. plus haut.
# * la meilleure solution vis à vis du temps de calcul est d'utiliser $m = M$, ie. la table de hachage est juste un vecteur de bit, où la case $j$ vaut $T[j]=[j]$ ssi $j$ est dans la table. Chaque entier est stocké dans sa propre liste, de taille vide ou de taille 1. On a donc une complexité en $O(1)$ pour les opérations de base, cf. plus haut.
# * choisir un $m$ intermédiaire, par exemple $m = O(\log(M))$, peut permettre de balancer entre les deux extrêmes.
#
# - Pour des chaînes de caractères, on peut faire la somme des hachés de chaque caractères, modulo un certain nombre, ou n'importe quelle idée de ce genre.
#
# - Python utilise la fonction `hash()` :
# In[28]:
help(hash)
# In[29]:
hash(1) # les entiers suffisamment petits sont hachés sur eux même
hash(2**2399)
hash("1")
# In[30]:
hash("Réfléchissez à l'impact écologique de TOUS les aspects de votre vie !")
# - Les détails d'implémentations de `hash` vont au delà de la portée de ce cours.
# - Voir [cette démonstration](http://people.irisa.fr/Francois.Schwarzentruber/hash_tables_demo/) pour des exemples de fonctions de hachage.
# ### Pour l'exemple ici
# - Pour l'implémentation ici, on va utiliser la fonction `f(x) = hash(x) % m`, où `taille` sera un paramètre de la table.
# - L'avantage est que l'on pourra stocker n'importe quel objet Python (enfin, n'importe quel objet hachable, cf. [cette explication](https://stackoverflow.com/questions/14535730/what-does-hashable-mean-in-python)).
#
# In[31]:
def homemadeHash(m=1024):
def f(x):
return hash(x) % m
return f
# In[32]:
class SetWithHashTable(SetWithNonPrimOperations):
""" Hash table with linked chaining: each cell uses a Python list to store the values."""
sizeMax = 1024
def __init__(self, size=sizeMax):
""" Create a new empty hash table."""
self.size = size
self.hash = homemadeHash(size)
self.table = [ [] for _ in range(self.size) ]
def __len__(self):
""" Return n the current size of the set.
- Takes O(m) time in all cases.
"""
return sum(len(cell) for cell in self.table)
def contains(self, value):
""" Test if value is in the set.
- Takes O(k) for k the length of the cell containing the value.
"""
k = self.hash(value)
return value in self.table[k]
__contains__ = contains
def add(self, value):
""" Add value in the set if it is not present."""
k = self.hash(value)
if value not in self.table[k]:
self.table[k].append(value)
def pop(self, value):
""" Remove value in the set if it is present."""
k = self.hash(value)
if value in self.table[k]:
self.table[k].remove(value)
def values(self):
""" Return a fresh list of the values of the set.
- Takes O(n) time in worst case."""
values = []
for cell in self.table:
for value in cell:
values.append(value)
return values
# In[33]:
un_petit_test_avec_une_structure_densemble(SetWithHashTable)
# Et maintenant quelques tests :
# In[34]:
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithHashTable, size=10, max_value=10, min_value=0)')
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithHashTable, size=10, max_value=1000, min_value=0)')
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithHashTable, size=1000, max_value=10, min_value=0)')
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithHashTable, size=100, max_value=100, min_value=0)')
# In[35]:
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithHashTable, size=1000, max_value=1000, min_value=0)')
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithHashTable, size=1000, max_value=1000_000, min_value=0)')
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithHashTable, size=1000, max_value=1000_000_000, min_value=0)')
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithHashTable, size=1000, max_value=1000_000_000_000, min_value=0)')
# La complexité (amortie) des opérations semble aussi indépendant de la taille des valeurs hachées (c'est logique, vu le modulo dans la fonction $f(x)$), et linéaire dans la taille des ensembles.
# In[36]:
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithHashTable, size=1000_000, max_value=1000, min_value=0)')
#%timeit random_add_remove_test(SetWithHashTable, size=1000_000, max_value=1000_000, min_value=0)
#%timeit random_add_remove_test(SetWithHashTable, size=1000_000, max_value=1000_000_000, min_value=0)
#%timeit random_add_remove_test(SetWithHashTable, size=1000_000, max_value=1000_000_000_000, min_value=0)
# On montre plus bas que cette implémentation "maison" en pure Python est raisonnablement efficace !
# ----
# ## Implémentation avec des arbres binaires de recherche ?
#
# Pour plus de détails sur les arbres binaires de recherche, cf. le cours, le chapitre 12 du livre de référence "Algorithmique" de Cormen et al, et sur Internet.
#
#
#
# Les opérations de base sur l'ensemble représenté par la table seront réalisées comme suit :
#
# - Lorsqu'on ajoute une valeur $v$ à la table :
# + on calcule $j = f(v)$,
# + on ajoute $v$ à l'ensemble en position $j$ du tableau :
# * si c'est une liste chaînée par exemple, on créée une nouvelle liste contenant $v$ ou on ajoute $v$ à la fin de la liste chaînée,
# * si c'est une autre table de hachage, on l'ajoute en utilisant la primitive de la table,
# * etc
#
# - Lorsque l'on veut tester l'appartenance de $v$ à la table :
# + on calcule $j = f(v)$ (le numéro de la cellule contenant $v$, on parle parfois aussi d'alvéole),
# + on test si $v$ appartient à la liste / l'ensemble stocké en position $j$ du tableau.
#
# - La suppression fonctionne comme l'ajout.
# ### Comment stocker les plus petits ensembles ?
# - A première vue, on est face à une idée stupide : pour stocker un ensemble, on en stocke $m$…
# - Mais si la fonction de hachage est bien faite, si elle envoie les données $x \in D$ sur les $m$ différentes valeurs uniformément (en gros si $\forall j\in\{0,\dots,m\}, \# \{ x \in D : f(x) = j\} \simeq \frac{1}{m}$)
# - Les opérations de base sur les sous ensembles (les alvéoles) sont en complexités (au pire cas) linéaires dans la taille de ces sous ensembles, ce qui dépend du remplissage actuel de la table.
# Par exemple, avec $m = 20$, la fonction $f(x) = x \mod 20$ et des valeurs qui sont des entiers aléatoirement tirés (cf. [cette page de démonstration](http://people.irisa.fr/Francois.Schwarzentruber/hash_tables_demo/)) :
#
# 0 |_| --> []
# 1 |_| --> [98281,92581,11221]
# 2 |_| --> [91422,84022,65742,55322,59162]
# 3 |_| --> [64583,43563]
# 4 |_| --> []
# 5 |_| --> [1665,1585]
# 6 |_| --> [80986,80446,95966,28446,74726]
# 7 |_| --> [40867,86987,47907]
# 8 |_| --> [86268,31908,21688,59068,50448]
# 9 |_| --> [65989,38369,69769]
# 10 |_| --> [8670]
# 11 |_| --> [27211,99291]
# 12 |_| --> [43532]
# 13 |_| --> [55033,3873,76353]
# 14 |_| --> [74734]
# 15 |_| --> [36075,62495,42015,75435,26415]
# 16 |_| --> [85336,21856,18376,46436,64516]
# 17 |_| --> [66117,95857]
# 18 |_| --> [76438]
# 19 |_| --> []
#
# Par exemples :
# - Ici, chercher l'appartenance de 76438 à l'ensemble se fera en deux opérations : calculer $f(76438)=18$, puis en cherchant (en une seule opération) $76438$ dans `T[18]=` $[76438]$.
# - Chercher $59068$ va trouver la cellule $f(59068) = 8$, qui contient 5 valeurs, et donc trouver $59068$ dans la liste $[86268,31908,21688,59068,50448]$ prend quatre opérations.
# ### Choix de la fonction de hachage
# - Il existe plein de fonction de hachage pour différentes utilisations.
# - Pour des entiers, on peut prendre $f(x) = x \mod m$ et adapter $m$ en fonction des propriétés voulues par notre structure.
# + Plus $m$ est grand, plus les opérations seront rapides mais plus on consomme de mémoire, inversement un plus petit $m$ réduit l'impact mémoire mais augmente l'impact temps.
# + En fait, si nos entiers sont entre $0$ et $M$, on peut avoir les deux cas extrêmes suivants :
# * la pire solution vis à vis du temps de calcul est d'utiliser $m = 1$, tous les entiers sont stockés dans la même liste. On a donc une complexité en $O(n)$ pour les opérations de base, cf. plus haut.
# * la meilleure solution vis à vis du temps de calcul est d'utiliser $m = M$, ie. la table de hachage est juste un vecteur de bit, où la case $j$ vaut $T[j]=[j]$ ssi $j$ est dans la table. Chaque entier est stocké dans sa propre liste, de taille vide ou de taille 1. On a donc une complexité en $O(1)$ pour les opérations de base, cf. plus haut.
# * choisir un $m$ intermédiaire, par exemple $m = O(\log(M))$, peut permettre de balancer entre les deux extrêmes.
#
# - Pour des chaînes de caractères, on peut faire la somme des hachés de chaque caractères, modulo un certain nombre, ou n'importe quelle idée de ce genre.
#
# - Python utilise la fonction `hash()` :
# In[28]:
help(hash)
# In[29]:
hash(1) # les entiers suffisamment petits sont hachés sur eux même
hash(2**2399)
hash("1")
# In[30]:
hash("Réfléchissez à l'impact écologique de TOUS les aspects de votre vie !")
# - Les détails d'implémentations de `hash` vont au delà de la portée de ce cours.
# - Voir [cette démonstration](http://people.irisa.fr/Francois.Schwarzentruber/hash_tables_demo/) pour des exemples de fonctions de hachage.
# ### Pour l'exemple ici
# - Pour l'implémentation ici, on va utiliser la fonction `f(x) = hash(x) % m`, où `taille` sera un paramètre de la table.
# - L'avantage est que l'on pourra stocker n'importe quel objet Python (enfin, n'importe quel objet hachable, cf. [cette explication](https://stackoverflow.com/questions/14535730/what-does-hashable-mean-in-python)).
#
# In[31]:
def homemadeHash(m=1024):
def f(x):
return hash(x) % m
return f
# In[32]:
class SetWithHashTable(SetWithNonPrimOperations):
""" Hash table with linked chaining: each cell uses a Python list to store the values."""
sizeMax = 1024
def __init__(self, size=sizeMax):
""" Create a new empty hash table."""
self.size = size
self.hash = homemadeHash(size)
self.table = [ [] for _ in range(self.size) ]
def __len__(self):
""" Return n the current size of the set.
- Takes O(m) time in all cases.
"""
return sum(len(cell) for cell in self.table)
def contains(self, value):
""" Test if value is in the set.
- Takes O(k) for k the length of the cell containing the value.
"""
k = self.hash(value)
return value in self.table[k]
__contains__ = contains
def add(self, value):
""" Add value in the set if it is not present."""
k = self.hash(value)
if value not in self.table[k]:
self.table[k].append(value)
def pop(self, value):
""" Remove value in the set if it is present."""
k = self.hash(value)
if value in self.table[k]:
self.table[k].remove(value)
def values(self):
""" Return a fresh list of the values of the set.
- Takes O(n) time in worst case."""
values = []
for cell in self.table:
for value in cell:
values.append(value)
return values
# In[33]:
un_petit_test_avec_une_structure_densemble(SetWithHashTable)
# Et maintenant quelques tests :
# In[34]:
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithHashTable, size=10, max_value=10, min_value=0)')
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithHashTable, size=10, max_value=1000, min_value=0)')
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithHashTable, size=1000, max_value=10, min_value=0)')
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithHashTable, size=100, max_value=100, min_value=0)')
# In[35]:
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithHashTable, size=1000, max_value=1000, min_value=0)')
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithHashTable, size=1000, max_value=1000_000, min_value=0)')
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithHashTable, size=1000, max_value=1000_000_000, min_value=0)')
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithHashTable, size=1000, max_value=1000_000_000_000, min_value=0)')
# La complexité (amortie) des opérations semble aussi indépendant de la taille des valeurs hachées (c'est logique, vu le modulo dans la fonction $f(x)$), et linéaire dans la taille des ensembles.
# In[36]:
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithHashTable, size=1000_000, max_value=1000, min_value=0)')
#%timeit random_add_remove_test(SetWithHashTable, size=1000_000, max_value=1000_000, min_value=0)
#%timeit random_add_remove_test(SetWithHashTable, size=1000_000, max_value=1000_000_000, min_value=0)
#%timeit random_add_remove_test(SetWithHashTable, size=1000_000, max_value=1000_000_000_000, min_value=0)
# On montre plus bas que cette implémentation "maison" en pure Python est raisonnablement efficace !
# ----
# ## Implémentation avec des arbres binaires de recherche ?
#
# Pour plus de détails sur les arbres binaires de recherche, cf. le cours, le chapitre 12 du livre de référence "Algorithmique" de Cormen et al, et sur Internet.
#
#  # ### Un nœud d'un arbre binaire
#
# - Un nœud contient une clé, `key`, et éventuellement une valeur associée,
# - Ainsi que des pointeurs vers d'autres nœuds (éventuellement) : parent, fils gauche (`left`) et fils droit (`right`).
# In[37]:
class NodeTree():
def __init__(self, key, value=None, left=None, right=None, parent=None):
self.key = key
self.value = value
self.left = left
self.right = right
self.parent = parent
def __str__(self):
if self.value is None: # key is also the stored value
return "{}".format(self.key)
else:
return "{}: {}".format(self.key, self.value)
# --- First algorithm on this BST: compute the height ---
def height(self):
""" Compute the height h of the Binary Search Tree.
- Takes a time in O(n). Could be stored and take a time O(1) but it's useless."""
h = 0
if self.left is not None:
h = max(h, 1 + self.left.height())
if self.right is not None:
h = max(h, 1 + self.right.height())
return h
# --- Keys and values ---
def keys(self):
""" Extract the keys from the Binary Search Tree.
- It is a generator, use list(self.keys()) to have a list.
- Takes a time in O(n) for n keys."""
if self is not None:
if self.left is not None:
yield from self.left.keys()
yield self.key
if self.right is not None:
yield from self.right.keys()
def values(self):
""" Extract the values from the Binary Search Tree.
- UIt is a generator, use list(self.keys()) to have a list.
- Takes a time in O(n) for n values."""
if self is not None:
if self.left is not None:
yield from self.left.values()
yield self.value
if self.right is not None:
yield from self.right.values()
# --- Search ---
def search(self, key):
""" Search for the NodeTree(...) associated to the queried key. Returns None if not found.
- Takes a time in O(h) = O(n) in worst case for n keys/values (if wrongly balanced)."""
if key is None or self.key is None:
raise KeyError
if self.key == key:
return self
elif key < self.key and self.left is not None:
return self.left.search(key)
elif key > self.key and self.right is not None:
return self.right.search(key)
raise KeyError
# --- Looking for minimum / successor ---
def minimum(self):
""" Search for the NodeTree(...) associated to the minimum key.
- Takes a time in O(h) = O(n) in worst case for n keys/values (if wrongly balanced)."""
if self.left is None:
return self
else:
return self.left.minimum()
def successor(self, node):
""" Search for the NodeTree(...) successor of the queried node (ie. the node with smallest key >= node.key).
- Takes a time in O(h) = O(n) in worst case for n keys/values (if wrongly balanced)."""
if node.right is not None:
return node.right.minimum()
x = node
y = x.parent
while y is not None and x == y.right():
x = y
y = x.parent
return y
# --- Looking for maximum / predecessor ---
def maximum(self):
""" Search for the NodeTree(...) associated to the maximum key.
- Takes a time in O(h) = O(n) in worst case for n keys/values (if wrongly balanced)."""
if self is None:
return self
else:
return self.right.maximum()
def predecessor(self, node):
""" Search for the NodeTree(...) predecessor of the queried node (ie. the node with largest key <= node.key).
- Takes a time in O(h) = O(n) in worst case for n keys/values (if wrongly balanced)."""
if node.left is not None:
return node.left.maximum()
x = node
y = x.parent
while y is not None and x == y.left():
x = y
y = x.parent
return y
# Les deux exemples de la figure se représentent comme ça :
# - Pour l'arbre équilibré de la figure (a) ci dessus :
# In[38]:
n_5 = NodeTree(5)
n_3 = NodeTree(3)
n_2 = NodeTree(2)
n_5bis = NodeTree(5)
n_7 = NodeTree(7)
n_8 = NodeTree(8)
n_5.left, n_5.right = n_3, n_7
n_3.left, n_3.right = n_2, n_5bis
n_7.right = n_8
n_3.parent, n_7.parent = n_5, n_5
n_2.parent, n_5bis.parent = n_3, n_3
n_8.parent = n_7
# - Pour l'arbre non équilibré de la figure (b) ci dessus :
# In[39]:
n_5 = NodeTree(5)
n_3 = NodeTree(3)
n_2 = NodeTree(2)
n_5bis = NodeTree(5)
n_7 = NodeTree(7)
n_8 = NodeTree(8)
n_2.right = n_3 ; n_3.parent = n_2
n_3.right = n_7 ; n_7.parent = n_3
n_7.left = n_5 ; n_5.parent = n_7
n_5.left = n_5bis ; n_5bis.parent = n_5
n_7.right = n_8 ; n_8.parent = n_7
# ### Un arbre binaire de recherche
# Et maintenant pour la classe :
# In[40]:
class BinarySearchTree():
def __init__(self):
self.root = None
self.size = 0
# --- Looking for a (key,value) ---
def get(self, key):
""" Search for the value associated to the queried key.
- Takes a time in O(h) = O(n) in worst case for n keys/values (if wrongly balanced)."""
if self.root is None:
raise KeyError
node = self.root.search(key)
if node is not None:
return node.value
raise KeyError
def contains(self, value):
""" Test if value is in the set.
- Takes O(h) for h the height of the BST.
"""
try:
_ = self.get(value)
return True
except KeyError:
return False
__contains__ = contains
# --- Looking for minimum / successor ---
def minimum(self):
""" Search for the NodeTree(...) associated to the minimum key.
- Takes a time in O(h) = O(n) in worst case for n keys/values (if wrongly balanced)."""
if self.root is not None:
return self.root.minimum()
raise KeyError
def successor(self, node):
""" Search for the NodeTree(...) successor of the queried node (ie. the node with smallest key >= node.key).
- Takes a time in O(h) = O(n) in worst case for n keys/values (if wrongly balanced)."""
if self.root is not None:
return self.root.successor(node)
raise KeyError
# --- Looking for maximum / predecessor ---
def maximum(self):
""" Search for the NodeTree(...) associated to the maximum key.
- Takes a time in O(h) = O(n) in worst case for n keys/values (if wrongly balanced)."""
if self.root is not None:
return self.root.maximum()
raise KeyError
def predecessor(self, node):
""" Search for the NodeTree(...) predecessor of the queried node (ie. the node with largest key <= node.key).
- Takes a time in O(h) = O(n) in worst case for n keys/values (if wrongly balanced)."""
if self.root is not None:
return self.root.predecessor(node)
raise KeyError
# --- Insertion ---
def insert(self, key, value=None):
""" Insert a new key (or (key, value)) in the BST.
- Takes a time in O(h) = O(n) in worst case for n keys/values (if wrongly balanced)."""
if key in self:
value_mapped = self.get(key)
if value == value_mapped:
return # nothing to do, the pair (key, value) is already in the set!
self.size += 1
z = NodeTree(key, value=value)
y = None
x = self.root
while x is not None:
y = x
if z.key < x.key:
x = x.left
else:
x = x.right
z.parent = y
if y is None: # the tree was empty!
self.root = z
elif z.key < y.key:
y.left = z
else:
y.right = z
# --- Supression/deletion: it is harder! ---
def delete(self, key):
""" Delete the key in the BST.
- Takes a time in O(h) = O(n) in worst case for n keys/values (if wrongly balanced)."""
if self.root is None:
raise KeyError
node_to_delete = self.root.search(key)
if node_to_delete is None:
raise KeyError
self.size -= 1
z = node_to_delete
# ligne 1-3 Cormen [Arbre-Supprimer]
if z.left is None or z.right is None:
y = z
else:
y = self.successor(z)
# ligne 4-6 Cormen [Arbre-Supprimer]
if y.left is not None:
x = y.left
else:
x = y.right
# ligne 7-8 Cormen [Arbre-Supprimer]
if x is not None:
x.parent = y.parent
# ligne 9-13 Cormen [Arbre-Supprimer]
if y.parent is None:
self.root = x
elif y == y.parent.left:
y.parent.left = x
else:
y.parent.right = x
# ligne 14-16 Cormen [Arbre-Supprimer]
if y != z:
z.key, z.value = y.key, y.value
return y
# --- Keys and values ---
def keys(self):
""" Extract the keys from the Binary Search Tree.
- Takes a time in O(n) for n keys."""
if self.root is not None:
return list(self.root.keys())
return []
def values(self):
""" Extract the values from the Binary Search Tree.
- Takes a time in O(n) for n values."""
if self.root is not None:
return list(self.root.values())
return []
# --- Length, height ---
def __len__(self):
return self.size
def height(self):
if self.root is not None:
return self.root.height()
else:
return -1
# --- Draw the graph ---
def to_nxgraph(self):
G = nx.DiGraph()
def go_down(node):
if node.left is not None:
G.add_node(node.left)
G.add_edge(node, node.left)
go_down(node.left)
if node.right is not None:
G.add_node(node.right)
G.add_edge(node, node.right)
go_down(node.right)
if self.root is not None:
G.add_node(self.root)
go_down(self.root)
return G
def plot(self):
G = self.to_nxgraph()
pos = nx.drawing.nx_agraph.graphviz_layout(G, prog='dot')
return nx.draw(G, pos, with_labels=True)
# Dessiner l'ABR est facile, avec la bibliothèque [NetworkX](https://networkx.github.io/).
# In[41]:
import matplotlib.pyplot as plt
import networkx as nx
# Quelques exemples et quelques tests :
# In[42]:
keys = list(range(10))
values = [ "V{}".format(key) for key in keys ]
# In[43]:
BST = BinarySearchTree()
for (k, v) in zip(keys, values):
print("Clés de l'ABR =", list(BST.keys()), "Valeurs de l'ABR =", list(BST.values()), "Hauteur de l'ABR =", BST.height(), "Taille de l'ABR =", BST.size)
BST.insert(k, v)
print("Clés de l'ABR =", list(BST.keys()), "Valeurs de l'ABR =", list(BST.values()), "Hauteur de l'ABR =", BST.height(), "Taille de l'ABR =", BST.size)
# In[44]:
BST.plot()
# Maintenant si l'ordre d'insertion des clés n'est plus monotone, on va éviter d'avoir un arbre binaire réduit à une chaîne.
# In[45]:
BST = BinarySearchTree()
keys_values = list(zip(keys, values))
import random
random.seed(1234)
random.shuffle(keys_values)
print("Clés et valeurs =", keys_values)
for (k, v) in keys_values:
BST.insert(k, v)
print("Clés de l'ABR =", list(BST.keys()), "Valeurs de l'ABR =", list(BST.values()), "Hauteur de l'ABR =", BST.height(), "Taille de l'ABR =", BST.size)
for k in keys:
print("Valeur associée à", k, "=", BST.get(k))
# In[46]:
BST.plot()
# On voit ici que si on insert les clés dans un ordre "aléatoire" (ie. un ordre qui a peu de chance de donner un cas trop dégénéré), l'arbre binaire ne sera *pas* réduit à une chaîne et il aura une hauteur bien plus faible que sa taille.
# ### Ensemble avec un Arbre Binaire de Recherche
#
# C'est très simple, on va stocker les valeurs de l'ensemble dans les clés de l'ABR et on utilise des valeurs vides.
#
# L'objectif est d'avoir une complexité en $\mathcal{O}(\log(n))$ pour l'ajout, l'appartenance et le retrait de valeurs, si les valeurs ajoutées sont insérées dans un ordre aléatoire.
# Comme pour la table de hachage, la complexité au pire des cas restera linéaire en $\Omega(n)$ (si on construit un ABR réduit à une chaîne linéaire, comme l'exemple plus haut).
# In[47]:
class SetWithBinarySearchTree(BinarySearchTree, SetWithNonPrimOperations):
""" A set storing its values in a Binary Search Tree."""
def values(self): # hack: we only use keys as values
return self.keys()
def add(self, value):
""" Add value in the set if it is not present."""
key, value = value, None
return self.insert(key, value=value)
def pop(self, value):
""" Remove value in the set if it is present."""
return self.delete(value)
# Et pour la dernière structure implémentée ici, on teste :
# In[48]:
un_petit_test_avec_une_structure_densemble(SetWithBinarySearchTree)
# Et maintenant quelques tests :
# In[49]:
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithBinarySearchTree, size=10, max_value=10, min_value=0)')
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithBinarySearchTree, size=10, max_value=1000, min_value=0)')
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithBinarySearchTree, size=1000, max_value=10, min_value=0)')
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithBinarySearchTree, size=100, max_value=100, min_value=0)')
# In[50]:
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithBinarySearchTree, size=100, max_value=1000_000, min_value=-1000_000)')
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithBinarySearchTree, size=1000, max_value=1000_000, min_value=-1000_000)')
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithBinarySearchTree, size=10000, max_value=1000_000, min_value=-1000_000)')
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithBinarySearchTree, size=100000, max_value=1000_000, min_value=-1000_000)')
# ## Comparaison des différentes implémentations
# In[51]:
print("\n- Pour la classe", NativeSet)
get_ipython().run_line_magic('timeit', 'random_add_remove_test(NativeSet, size=1000, max_value=1000_000, min_value=0)')
print("\n- Pour la classe", SetWithList)
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithList, size=1000, max_value=1000_000, min_value=0)')
print("\n- Pour la classe", SetWithInt)
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithInt, size=1000, max_value=1000_000, min_value=0)')
print("\n- Pour la classe", SetWithHashTable)
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithHashTable, size=1000, max_value=1000_000, min_value=0)')
print("\n- Pour la classe", SetWithBinarySearchTree)
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithBinarySearchTree, size=1000, max_value=1000_000, min_value=0)')
# In[52]:
print("\n- Pour la classe", NativeSet)
get_ipython().run_line_magic('timeit', 'random_add_remove_test(NativeSet, size=10_000, max_value=1000_000, min_value=0)')
print("\n- Pour la classe", SetWithList)
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithList, size=10_000, max_value=1000_000, min_value=0)')
print("\n- Pour la classe", SetWithHashTable)
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithHashTable, size=10_000, max_value=1000_000, min_value=0)')
print("\n- Pour la classe", SetWithBinarySearchTree)
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithBinarySearchTree, size=10_000, max_value=1000_000, min_value=0)')
# In[53]:
print("\n- Pour la classe", NativeSet)
get_ipython().run_line_magic('timeit', 'random_add_remove_test(NativeSet, size=20_000, max_value=1000_000, min_value=0)')
print("\n- Pour la classe", SetWithList)
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithList, size=20_000, max_value=1000_000, min_value=0)')
print("\n- Pour la classe", SetWithHashTable)
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithHashTable, size=20_000, max_value=1000_000, min_value=0)')
print("\n- Pour la classe", SetWithBinarySearchTree)
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithBinarySearchTree, size=20_000, max_value=1000_000, min_value=0)')
# In[56]:
print("\n- Pour la classe", NativeSet)
get_ipython().run_line_magic('timeit', 'random_add_remove_test(NativeSet, size=30_000, max_value=1000_000, min_value=0)')
print("\n- Pour la classe", SetWithList)
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithList, size=30_000, max_value=1000_000, min_value=0)')
print("\n- Pour la classe", SetWithHashTable)
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithHashTable, size=30_000, max_value=1000_000, min_value=0)')
print("\n- Pour la classe", SetWithBinarySearchTree)
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithBinarySearchTree, size=30_000, max_value=1000_000, min_value=0)')
# On voit que notre implémentation "maison" avec des tables de hachage est quasiment aussi efficace que l'implémentation native (en C !) de Python avec la classe `set` (qui utilise aussi une table de hachage, mais écrite en C !).
# ## Conclusion
#
# C'est bon pour aujourd'hui !
# ### Un nœud d'un arbre binaire
#
# - Un nœud contient une clé, `key`, et éventuellement une valeur associée,
# - Ainsi que des pointeurs vers d'autres nœuds (éventuellement) : parent, fils gauche (`left`) et fils droit (`right`).
# In[37]:
class NodeTree():
def __init__(self, key, value=None, left=None, right=None, parent=None):
self.key = key
self.value = value
self.left = left
self.right = right
self.parent = parent
def __str__(self):
if self.value is None: # key is also the stored value
return "{}".format(self.key)
else:
return "{}: {}".format(self.key, self.value)
# --- First algorithm on this BST: compute the height ---
def height(self):
""" Compute the height h of the Binary Search Tree.
- Takes a time in O(n). Could be stored and take a time O(1) but it's useless."""
h = 0
if self.left is not None:
h = max(h, 1 + self.left.height())
if self.right is not None:
h = max(h, 1 + self.right.height())
return h
# --- Keys and values ---
def keys(self):
""" Extract the keys from the Binary Search Tree.
- It is a generator, use list(self.keys()) to have a list.
- Takes a time in O(n) for n keys."""
if self is not None:
if self.left is not None:
yield from self.left.keys()
yield self.key
if self.right is not None:
yield from self.right.keys()
def values(self):
""" Extract the values from the Binary Search Tree.
- UIt is a generator, use list(self.keys()) to have a list.
- Takes a time in O(n) for n values."""
if self is not None:
if self.left is not None:
yield from self.left.values()
yield self.value
if self.right is not None:
yield from self.right.values()
# --- Search ---
def search(self, key):
""" Search for the NodeTree(...) associated to the queried key. Returns None if not found.
- Takes a time in O(h) = O(n) in worst case for n keys/values (if wrongly balanced)."""
if key is None or self.key is None:
raise KeyError
if self.key == key:
return self
elif key < self.key and self.left is not None:
return self.left.search(key)
elif key > self.key and self.right is not None:
return self.right.search(key)
raise KeyError
# --- Looking for minimum / successor ---
def minimum(self):
""" Search for the NodeTree(...) associated to the minimum key.
- Takes a time in O(h) = O(n) in worst case for n keys/values (if wrongly balanced)."""
if self.left is None:
return self
else:
return self.left.minimum()
def successor(self, node):
""" Search for the NodeTree(...) successor of the queried node (ie. the node with smallest key >= node.key).
- Takes a time in O(h) = O(n) in worst case for n keys/values (if wrongly balanced)."""
if node.right is not None:
return node.right.minimum()
x = node
y = x.parent
while y is not None and x == y.right():
x = y
y = x.parent
return y
# --- Looking for maximum / predecessor ---
def maximum(self):
""" Search for the NodeTree(...) associated to the maximum key.
- Takes a time in O(h) = O(n) in worst case for n keys/values (if wrongly balanced)."""
if self is None:
return self
else:
return self.right.maximum()
def predecessor(self, node):
""" Search for the NodeTree(...) predecessor of the queried node (ie. the node with largest key <= node.key).
- Takes a time in O(h) = O(n) in worst case for n keys/values (if wrongly balanced)."""
if node.left is not None:
return node.left.maximum()
x = node
y = x.parent
while y is not None and x == y.left():
x = y
y = x.parent
return y
# Les deux exemples de la figure se représentent comme ça :
# - Pour l'arbre équilibré de la figure (a) ci dessus :
# In[38]:
n_5 = NodeTree(5)
n_3 = NodeTree(3)
n_2 = NodeTree(2)
n_5bis = NodeTree(5)
n_7 = NodeTree(7)
n_8 = NodeTree(8)
n_5.left, n_5.right = n_3, n_7
n_3.left, n_3.right = n_2, n_5bis
n_7.right = n_8
n_3.parent, n_7.parent = n_5, n_5
n_2.parent, n_5bis.parent = n_3, n_3
n_8.parent = n_7
# - Pour l'arbre non équilibré de la figure (b) ci dessus :
# In[39]:
n_5 = NodeTree(5)
n_3 = NodeTree(3)
n_2 = NodeTree(2)
n_5bis = NodeTree(5)
n_7 = NodeTree(7)
n_8 = NodeTree(8)
n_2.right = n_3 ; n_3.parent = n_2
n_3.right = n_7 ; n_7.parent = n_3
n_7.left = n_5 ; n_5.parent = n_7
n_5.left = n_5bis ; n_5bis.parent = n_5
n_7.right = n_8 ; n_8.parent = n_7
# ### Un arbre binaire de recherche
# Et maintenant pour la classe :
# In[40]:
class BinarySearchTree():
def __init__(self):
self.root = None
self.size = 0
# --- Looking for a (key,value) ---
def get(self, key):
""" Search for the value associated to the queried key.
- Takes a time in O(h) = O(n) in worst case for n keys/values (if wrongly balanced)."""
if self.root is None:
raise KeyError
node = self.root.search(key)
if node is not None:
return node.value
raise KeyError
def contains(self, value):
""" Test if value is in the set.
- Takes O(h) for h the height of the BST.
"""
try:
_ = self.get(value)
return True
except KeyError:
return False
__contains__ = contains
# --- Looking for minimum / successor ---
def minimum(self):
""" Search for the NodeTree(...) associated to the minimum key.
- Takes a time in O(h) = O(n) in worst case for n keys/values (if wrongly balanced)."""
if self.root is not None:
return self.root.minimum()
raise KeyError
def successor(self, node):
""" Search for the NodeTree(...) successor of the queried node (ie. the node with smallest key >= node.key).
- Takes a time in O(h) = O(n) in worst case for n keys/values (if wrongly balanced)."""
if self.root is not None:
return self.root.successor(node)
raise KeyError
# --- Looking for maximum / predecessor ---
def maximum(self):
""" Search for the NodeTree(...) associated to the maximum key.
- Takes a time in O(h) = O(n) in worst case for n keys/values (if wrongly balanced)."""
if self.root is not None:
return self.root.maximum()
raise KeyError
def predecessor(self, node):
""" Search for the NodeTree(...) predecessor of the queried node (ie. the node with largest key <= node.key).
- Takes a time in O(h) = O(n) in worst case for n keys/values (if wrongly balanced)."""
if self.root is not None:
return self.root.predecessor(node)
raise KeyError
# --- Insertion ---
def insert(self, key, value=None):
""" Insert a new key (or (key, value)) in the BST.
- Takes a time in O(h) = O(n) in worst case for n keys/values (if wrongly balanced)."""
if key in self:
value_mapped = self.get(key)
if value == value_mapped:
return # nothing to do, the pair (key, value) is already in the set!
self.size += 1
z = NodeTree(key, value=value)
y = None
x = self.root
while x is not None:
y = x
if z.key < x.key:
x = x.left
else:
x = x.right
z.parent = y
if y is None: # the tree was empty!
self.root = z
elif z.key < y.key:
y.left = z
else:
y.right = z
# --- Supression/deletion: it is harder! ---
def delete(self, key):
""" Delete the key in the BST.
- Takes a time in O(h) = O(n) in worst case for n keys/values (if wrongly balanced)."""
if self.root is None:
raise KeyError
node_to_delete = self.root.search(key)
if node_to_delete is None:
raise KeyError
self.size -= 1
z = node_to_delete
# ligne 1-3 Cormen [Arbre-Supprimer]
if z.left is None or z.right is None:
y = z
else:
y = self.successor(z)
# ligne 4-6 Cormen [Arbre-Supprimer]
if y.left is not None:
x = y.left
else:
x = y.right
# ligne 7-8 Cormen [Arbre-Supprimer]
if x is not None:
x.parent = y.parent
# ligne 9-13 Cormen [Arbre-Supprimer]
if y.parent is None:
self.root = x
elif y == y.parent.left:
y.parent.left = x
else:
y.parent.right = x
# ligne 14-16 Cormen [Arbre-Supprimer]
if y != z:
z.key, z.value = y.key, y.value
return y
# --- Keys and values ---
def keys(self):
""" Extract the keys from the Binary Search Tree.
- Takes a time in O(n) for n keys."""
if self.root is not None:
return list(self.root.keys())
return []
def values(self):
""" Extract the values from the Binary Search Tree.
- Takes a time in O(n) for n values."""
if self.root is not None:
return list(self.root.values())
return []
# --- Length, height ---
def __len__(self):
return self.size
def height(self):
if self.root is not None:
return self.root.height()
else:
return -1
# --- Draw the graph ---
def to_nxgraph(self):
G = nx.DiGraph()
def go_down(node):
if node.left is not None:
G.add_node(node.left)
G.add_edge(node, node.left)
go_down(node.left)
if node.right is not None:
G.add_node(node.right)
G.add_edge(node, node.right)
go_down(node.right)
if self.root is not None:
G.add_node(self.root)
go_down(self.root)
return G
def plot(self):
G = self.to_nxgraph()
pos = nx.drawing.nx_agraph.graphviz_layout(G, prog='dot')
return nx.draw(G, pos, with_labels=True)
# Dessiner l'ABR est facile, avec la bibliothèque [NetworkX](https://networkx.github.io/).
# In[41]:
import matplotlib.pyplot as plt
import networkx as nx
# Quelques exemples et quelques tests :
# In[42]:
keys = list(range(10))
values = [ "V{}".format(key) for key in keys ]
# In[43]:
BST = BinarySearchTree()
for (k, v) in zip(keys, values):
print("Clés de l'ABR =", list(BST.keys()), "Valeurs de l'ABR =", list(BST.values()), "Hauteur de l'ABR =", BST.height(), "Taille de l'ABR =", BST.size)
BST.insert(k, v)
print("Clés de l'ABR =", list(BST.keys()), "Valeurs de l'ABR =", list(BST.values()), "Hauteur de l'ABR =", BST.height(), "Taille de l'ABR =", BST.size)
# In[44]:
BST.plot()
# Maintenant si l'ordre d'insertion des clés n'est plus monotone, on va éviter d'avoir un arbre binaire réduit à une chaîne.
# In[45]:
BST = BinarySearchTree()
keys_values = list(zip(keys, values))
import random
random.seed(1234)
random.shuffle(keys_values)
print("Clés et valeurs =", keys_values)
for (k, v) in keys_values:
BST.insert(k, v)
print("Clés de l'ABR =", list(BST.keys()), "Valeurs de l'ABR =", list(BST.values()), "Hauteur de l'ABR =", BST.height(), "Taille de l'ABR =", BST.size)
for k in keys:
print("Valeur associée à", k, "=", BST.get(k))
# In[46]:
BST.plot()
# On voit ici que si on insert les clés dans un ordre "aléatoire" (ie. un ordre qui a peu de chance de donner un cas trop dégénéré), l'arbre binaire ne sera *pas* réduit à une chaîne et il aura une hauteur bien plus faible que sa taille.
# ### Ensemble avec un Arbre Binaire de Recherche
#
# C'est très simple, on va stocker les valeurs de l'ensemble dans les clés de l'ABR et on utilise des valeurs vides.
#
# L'objectif est d'avoir une complexité en $\mathcal{O}(\log(n))$ pour l'ajout, l'appartenance et le retrait de valeurs, si les valeurs ajoutées sont insérées dans un ordre aléatoire.
# Comme pour la table de hachage, la complexité au pire des cas restera linéaire en $\Omega(n)$ (si on construit un ABR réduit à une chaîne linéaire, comme l'exemple plus haut).
# In[47]:
class SetWithBinarySearchTree(BinarySearchTree, SetWithNonPrimOperations):
""" A set storing its values in a Binary Search Tree."""
def values(self): # hack: we only use keys as values
return self.keys()
def add(self, value):
""" Add value in the set if it is not present."""
key, value = value, None
return self.insert(key, value=value)
def pop(self, value):
""" Remove value in the set if it is present."""
return self.delete(value)
# Et pour la dernière structure implémentée ici, on teste :
# In[48]:
un_petit_test_avec_une_structure_densemble(SetWithBinarySearchTree)
# Et maintenant quelques tests :
# In[49]:
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithBinarySearchTree, size=10, max_value=10, min_value=0)')
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithBinarySearchTree, size=10, max_value=1000, min_value=0)')
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithBinarySearchTree, size=1000, max_value=10, min_value=0)')
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithBinarySearchTree, size=100, max_value=100, min_value=0)')
# In[50]:
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithBinarySearchTree, size=100, max_value=1000_000, min_value=-1000_000)')
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithBinarySearchTree, size=1000, max_value=1000_000, min_value=-1000_000)')
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithBinarySearchTree, size=10000, max_value=1000_000, min_value=-1000_000)')
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithBinarySearchTree, size=100000, max_value=1000_000, min_value=-1000_000)')
# ## Comparaison des différentes implémentations
# In[51]:
print("\n- Pour la classe", NativeSet)
get_ipython().run_line_magic('timeit', 'random_add_remove_test(NativeSet, size=1000, max_value=1000_000, min_value=0)')
print("\n- Pour la classe", SetWithList)
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithList, size=1000, max_value=1000_000, min_value=0)')
print("\n- Pour la classe", SetWithInt)
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithInt, size=1000, max_value=1000_000, min_value=0)')
print("\n- Pour la classe", SetWithHashTable)
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithHashTable, size=1000, max_value=1000_000, min_value=0)')
print("\n- Pour la classe", SetWithBinarySearchTree)
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithBinarySearchTree, size=1000, max_value=1000_000, min_value=0)')
# In[52]:
print("\n- Pour la classe", NativeSet)
get_ipython().run_line_magic('timeit', 'random_add_remove_test(NativeSet, size=10_000, max_value=1000_000, min_value=0)')
print("\n- Pour la classe", SetWithList)
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithList, size=10_000, max_value=1000_000, min_value=0)')
print("\n- Pour la classe", SetWithHashTable)
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithHashTable, size=10_000, max_value=1000_000, min_value=0)')
print("\n- Pour la classe", SetWithBinarySearchTree)
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithBinarySearchTree, size=10_000, max_value=1000_000, min_value=0)')
# In[53]:
print("\n- Pour la classe", NativeSet)
get_ipython().run_line_magic('timeit', 'random_add_remove_test(NativeSet, size=20_000, max_value=1000_000, min_value=0)')
print("\n- Pour la classe", SetWithList)
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithList, size=20_000, max_value=1000_000, min_value=0)')
print("\n- Pour la classe", SetWithHashTable)
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithHashTable, size=20_000, max_value=1000_000, min_value=0)')
print("\n- Pour la classe", SetWithBinarySearchTree)
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithBinarySearchTree, size=20_000, max_value=1000_000, min_value=0)')
# In[56]:
print("\n- Pour la classe", NativeSet)
get_ipython().run_line_magic('timeit', 'random_add_remove_test(NativeSet, size=30_000, max_value=1000_000, min_value=0)')
print("\n- Pour la classe", SetWithList)
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithList, size=30_000, max_value=1000_000, min_value=0)')
print("\n- Pour la classe", SetWithHashTable)
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithHashTable, size=30_000, max_value=1000_000, min_value=0)')
print("\n- Pour la classe", SetWithBinarySearchTree)
get_ipython().run_line_magic('timeit', 'random_add_remove_test(SetWithBinarySearchTree, size=30_000, max_value=1000_000, min_value=0)')
# On voit que notre implémentation "maison" avec des tables de hachage est quasiment aussi efficace que l'implémentation native (en C !) de Python avec la classe `set` (qui utilise aussi une table de hachage, mais écrite en C !).
# ## Conclusion
#
# C'est bon pour aujourd'hui !